非线性数据结构之图
一、有向图(Directed Graph)
1. 定义
有向图是一个由顶点(节点)和有方向的边(弧)组成的图。在有向图中,每条边都有一个起点和一个终点,表示从一个顶点到另一个顶点的关系。
2. 特点
- 边有方向:每条边都有一个方向,通常用箭头表示。例如,边 A→B 表示从顶点 A 到顶点 B。
- 可能存在孤立点:有向图中的某些顶点可能没有入边或出边。
- 可有多个入度和出度:顶点的入度是指指向该顶点的边数,出度是指从该顶点出发的边数。
3. 优缺点
-
优点:
- 能够准确表示有向关系,如网页链接、任务调度等。
- 适合表示不对称的关系。
-
缺点:
- 复杂性较高,特别是在涉及遍历和路径寻找时。
- 算法实现相对复杂,如最短路径算法。
4. 应用场景
- 网络路由:表示计算机网络中的连接。
- 任务调度:表示任务之间的依赖关系。
- 图形界面:表示用户界面元素之间的交互。
5. 示例
有向图可以用邻接表或邻接矩阵表示。以下是一个有向图的示例:

示例代码(Java 实现)
import java.util.*;
class DirectedGraph {
private Map<String, List<String>> adjacencyList;
public DirectedGraph() {
adjacencyList = new HashMap<>();
}
public void addVertex(String vertex) {
adjacencyList.putIfAbsent(vertex, new ArrayList<>());
}
public void addEdge(String from, String to) {
adjacencyList.putIfAbsent(from, new ArrayList<>());
adjacencyList.putIfAbsent(to, new ArrayList<>());
adjacencyList.get(from).add(to);
}
public List<String> getNeighbors(String vertex) {
return adjacencyList.get(vertex);
}
}
二、无向图(Undirected Graph)
1. 定义
无向图是一个由顶点和无方向的边组成的图。在无向图中,边连接两个顶点,但没有方向。
2. 特点
- 边无方向:边表示的是两个顶点之间的关系,通常用线段表示。例如,边 A−B 表示顶点 A 和顶点 B 是相连的。
- 每条边相互对称:如果存在边 A−B,则同时存在边 B−A。
- 所有顶点具有相同的边关系。
3. 优缺点
-
优点:
- 适合表示对称关系,如社交网络、朋友关系。
- 较简单的算法实现。
-
缺点:
- 对于某些应用,缺乏表达方向性的能力。
- 在某些情况下,图的结构可能会显得过于简单。
4. 应用场景
- 社交网络:表示用户之间的朋友关系。
- 电路设计:表示电路中元件之间的连接。
- 城市交通:表示城市道路网络。
5. 示例
无向图可以用邻接表或邻接矩阵表示。以下是一个无向图的示例:

示例代码(Java 实现)
import java.util.*;
class UndirectedGraph {
private Map<String, List<String>> adjacencyList;
public UndirectedGraph() {
adjacencyList = new HashMap<>();
}
public void addVertex(String vertex) {
adjacencyList.putIfAbsent(vertex, new ArrayList<>());
}
public void addEdge(String vertex1, String vertex2) {
adjacencyList.putIfAbsent(vertex1, new ArrayList<>());
adjacencyList.putIfAbsent(vertex2, new ArrayList<>());
adjacencyList.get(vertex1).add(vertex2);
adjacencyList.get(vertex2).add(vertex1); // 无向边
}
public List<String> getNeighbors(String vertex) {
return adjacencyList.get(vertex);
}
}
三、加权图(Weighted Graph)
1. 定义
加权图是一个图,其中每条边都分配有一个权重(或成本)。权重可以表示距离、时间、费用等多种含义。
2. 特点
- 每条边有权重:边的权重通常是一个数值,表示从一个顶点到另一个顶点的代价。
- 支持最短路径计算:适合用于计算从一个顶点到另一个顶点的最短路径。
- 可以是有向或无向图:加权图可以是有向的或无向的。
3. 优缺点
-
优点:
- 能够表示复杂的关系,如交通网络、物流等。
- 可以使用多种算法(如 Dijkstra、Bellman-Ford)进行路径优化。
-
缺点:
- 处理复杂性较高,尤其是在大量边和顶点的情况下。
- 可能导致计算错误,尤其在负权重情况下(如 Bellman-Ford 算法)。
4. 应用场景
- 地图导航:用于计算从起点到终点的最短路径。
- 网络流量:分析和优化网络数据传输。
- 电路分析:计算电路中元件之间的电流和电压。
5. 示例
加权图的表示通常使用邻接表或邻接矩阵。以下是一个加权图的示例:
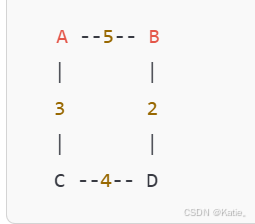
示例代码(Java 实现)
import java.util.*;
class WeightedGraph {
private Map<String, List<Edge>> adjacencyList;
class Edge {
String destination;
int weight;
Edge(String destination, int weight) {
this.destination = destination;
this.weight = weight;
}
}
public WeightedGraph() {
adjacencyList = new HashMap<>();
}
public void addVertex(String vertex) {
adjacencyList.putIfAbsent(vertex, new ArrayList<>());
}
public void addEdge(String from, String to, int weight) {
adjacencyList.putIfAbsent(from, new ArrayList<>());
adjacencyList.putIfAbsent(to, new ArrayList<>());
adjacencyList.get(from).add(new Edge(to, weight));
adjacencyList.get(to).add(new Edge(from, weight)); // 如果是无向图
}
public List<Edge> getNeighbors(String vertex) {
return adjacencyList.get(vertex);
}
}
总结比较
| 图类型 | 边的方向性 | 权重 | 适用场景 |
|---|---|---|---|
| 有向图 | 有方向 | 无 | 任务调度、网络路由 |
| 无向图 | 无方向 | 无 | 社交网络、城市交通 |
| 加权图 | 有向/无向 | 有 | 地图导航、网络流量、电路分析 |
通过这些详细的介绍,可以更清晰地理解不同图类型的特点和应用场景,为具体问题的解决选择合适的数据结构提供帮助。
