蓝桥杯专项---一维前缀/差分巩固题目

1.一维前缀和–区间的次方求和问题

下面的这个是分为了两个情况，这个0，1指的是我们的这个循环的初始值是从哪一个数字开始的：

1.1下面的这个是从0开始的：

刚开始就是读取这两个整数，第一个整数就是我们的这个数组的个数，第二个整数就是我们的这个查询的次数，然后是使用循环对于这个数组元素进行读取；

递推公式：表示的就是前面的j个元素的i次方和等于前面的j-1个元素的i次方和加上我们的第j个元素的i次方和

import java.util.Scanner;

public class 区间次方和 {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int n= sc.nextInt();
        int m= sc.nextInt();
        int []arr=new int[n];
        long mod=(long)1e9+7;
        for (int i = 0; i < n; i++) {
            arr[i]= sc.nextInt();
        }
        long [][]sum=new long[6][n+1];//防止溢出,此二维数组记录所有元素的k次方和,利用前缀和计算
        for(int i=1;i<=5;i++){//因为k的取值是1~5,所以把所有情况前缀和
            for (int j = 1; j <= n; j++) {
                sum[i][j]=sum[i][j-1]+(long)Math.pow(arr[j-1],i);
            }
        }
        for (int i = 0; i < m; i++) {
            int l= sc.nextInt()-1;
            int r= sc.nextInt()-1;
            int k= sc.nextInt();
            System.out.println((sum[k][r+1]-sum[k][l]+mod)%mod);//前缀和公式,+mod防止是负数
        }
    }
}

1.2下面的这个是从1开始的

递推公式：表示的就是前面的j个元素的i次方和等于前面的j-1个元素的i次方和加上我们的第j个元素的i次方和

public class 区间次方和 {
    public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        int n= sc.nextInt();
        int m= sc.nextInt();
        int []arr=new int[n+1];
        long mod=(long)1e9+7;
        for (int i = 1; i <= n; i++) {
            arr[i]= sc.nextInt();
        }
        long [][]sum=new long[6][n+1];//防止溢出,此二维数组记录所有元素的k次方和,利用前缀和计算
        for(int i=1;i<=5;i++){//因为k的取值是1~5,所以把所有情况前缀和
            for (int j = 1; j <= n; j++) {
              //这个就是递推公式：表示的就是前面的j个元素的i次方和等于前面的j-1歌元素的i次方和加上我们的第j个元素的i次方和
                sum[i][j]=sum[i][j-1]+(long)Math.pow(arr[j],i);
            }
        }
        for (int i = 1; i <= m; i++) {
            int l= sc.nextInt();
            int r= sc.nextInt();
            int k= sc.nextInt();
            System.out.println((sum[k][r]-sum[k][l-1]+mod)%mod);//前缀和公式,+mod防止是负数
        }
    }

2.一维差分—小兰的操作

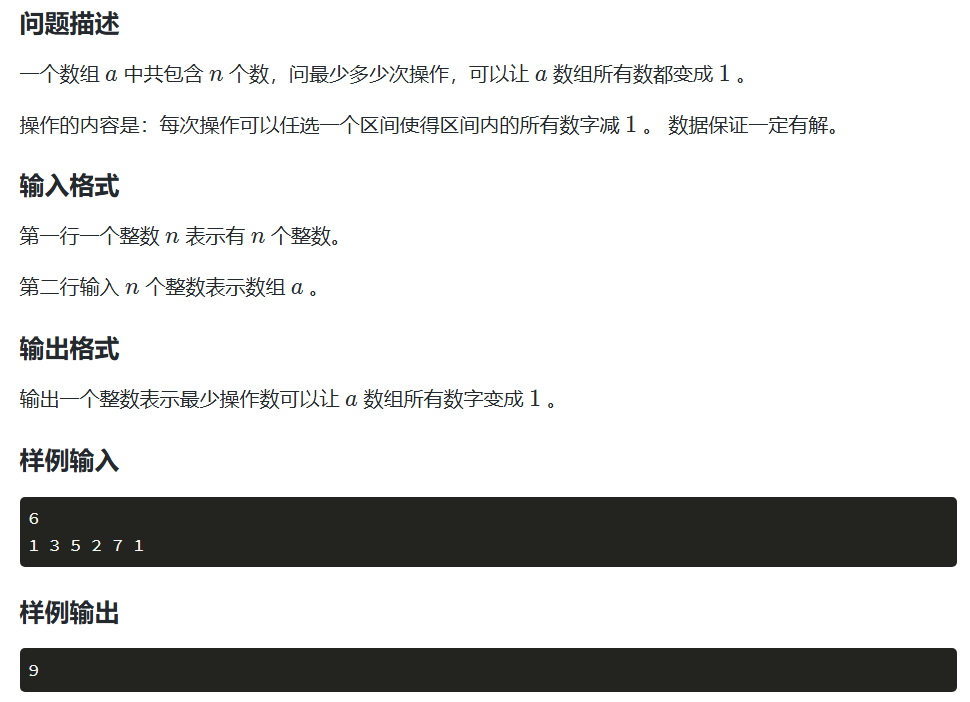
题目思路：先求解差分数组，再求解所有的正数的和，最后把这个所有的正数的和再减去一

1）差分数组：就是按照后面的一个减去前面的一个进行计算的，保存到新的数组里面去；

2）求解正数的和：就是我们需要使用这个if进行判断这个是不是正数，如果是的，就进行求和；

3）最后的这个结果是全部变为1操作的次数，而初始状态已经有一个1，所以实际需要的操作次数是 res - 1

import java.util.Scanner;

public class Main {
    static Scanner in = new Scanner(System.in);
    static int N = 100010;
    static int a[] = new int[N];
    static int b[] = new int[N];

    public static void main(String[] args) {
        solve();
    }

    static void solve() {
        int n = in.nextInt();
        long res = 0;
        for (int i = 1; i <= n; i++) {
            a[i] = in.nextInt();
            b[i] = a[i] - a[i-1];
            if (b[i] > 0) res += b[i];
        }
        System.out.println(res - 1);
    }
}

3.字符迁移

测试用例说明：这个测试用例其实是有一个计算的过程的，主要就是我们的这个abcde在这个基础上面不断地进行操作：

1）1-5这几个元素不断的加上3，这个实际上是这个ascii加上3，但是实际上按照这个字母序往后数3个就可以了，这个转换之后的结果就是：defgh；

2）1-2这两个元素往后查4个，这个转换之后的结果就是：hifgh;

3）2-5这几个元素往后查3位，这个转换之后的结果就是：hlijk；

这个题目的思路：

1）先读取整数，分别表示这个字符个数和这个查询的次数；

2）使用这个in.next()方法读取字符串，存储到这个str里面去；

3）把这个字符串转换为字符数组，方便我们的后续操作；

4）while就是读取这个查询的数据，例如从第几个开始，读取到什么位置，这个d[l]+=k;
d[r+1]-=k;就是我们的一维差分的常规操作，就是对于一个范围里面的数据就行加的操作；

5）我觉得这个题目里面的最难理解一个就是这个准换以及这个最后的d[i]+=d[i-1]的操作，因为我们的这个是把abcde这个字符数组转换为这个0,1,2,3,4这个数字数组，我们的的操作是基于这个数字数组进行操作的，这个是第一点；

d[i]=num[i]-num[i-1];这个是在进行这个差分数组的计算过程；

d[i]+=d[i-1];这个相当于是进行还原，因为我们最开始是基于这个差分数组操作的，但是我们的差分数组是减去前面的一项得到的，因此这个操作之后我们想要得到这个真实的数据，需要加上前面的一项进行还原（慢慢体会吧，确实挺难理解的，对于初学者而言，起码自己是这个样子的）

public class Main {
    static int N = (int)(2e5+10);

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n=in.nextInt();
        int m=in.nextInt();
        String str=in.next();
        char[] s=str.toCharArray();
        int[] num=new int[N];
        int[] d=new int[N];
        for(int i=1;i<=n;i++){
          num[i]=s[i-1]-'a';
          d[i]=num[i]-num[i-1];
        }

        while(m-->0){
          int l=in.nextInt();
          int r=in.nextInt();
          int k=in.nextInt();
          k%=26;
          d[l]+=k;
          d[r+1]-=k;
        }

        for(int i=1;i<=n;i++){
          d[i]+=d[i-1];
          System.out.print((char)(d[i]%26+'a'));
        }
        in.close();
    }
}

4.类一维前缀—第15届蓝桥杯真题—类斐波那契循环数

1）这个题目使用的是这个solve方法（在这个代码里面）；

2）第一个for循环就是获取这个数字转换为这个字符串之后的每一个元素；

3）这个里面可能会用到这个arraylist相关的一些api，例如这个add添加元素，remove删除元素，charAt取 出来这个对应下标的元素等等；

4）为什么是乘上2减去第一个元素，这个就是规律啊：上面的这个197案例里面。我们的这个=

33=17*2-1;这个时候就把这个数字1移除，我们的这个9成为了第一个元素

57=33*2-9;这个时候把这个9移除，我们的这个7成为了第一个元素；

107=57*2-7；这个时候移除7，17成为第一个元素，以此类推下去，这个就是这个题目的规律；

5）结合这个规律，我们使用这个remove表示一次操作之后移除数据的操作；

import java.util.ArrayList;
import java.util.Scanner;

public class Test {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        long an=0;
        for(int i=197;i<1e7;i++){
            if(pd(i)){
                an=i;
            }
        }
        System.out.println(an);
    }

    private static boolean pd(int i){
        ArrayList<Integer> ans = new ArrayList<>();
        String s=""+i;
        int anss=0;
        //转换为这个string方便获取每一个数位上面的证书
        for(int j=0;j<s.length();j++){
            //下面的这个ans就是我们的列表容器
            ans.add(s.charAt(j)-'0');
            anss=anss+s.charAt(j)-'0';
        }
        //上面的这个循环究竟是在干什么事情：下面的这个以1234为例子说明，方便理解
        //列表 ans 存储了整数 1234 的各个数位数字 [1, 2, 3, 4]，
        // 变量 anss 的值为 10，即整数 1234 各个数位数字的总和。

        ans.add(anss);
        //这个时候i的数组元素就是ans[1,2,3,4,10]
        while(true){
            //乘以2减去这个里面的第一个元素就是这个类斐波那契数列的规律，避免使用纯粹的数学方法计算
            anss=(anss*2)-ans.get(0);
            ans.remove(0);
            ans.add(anss);
            if(anss==i){
                return true;
            }else if(anss>i){
                return false;
            }
        }
    }
}