【智能算法应用】哈里斯鹰算法优化二维栅格路径规划问题

摘要
本文研究了基于哈里斯鹰优化算法(Harris Hawks Optimization, HHO)的二维栅格路径规划方法。HHO算法模拟哈里斯鹰的猎食行为,通过迭代搜索过程找到从起点到终点的最优路径,避开栅格中的障碍物。实验结果表明,HHO算法在路径平滑性和避障效率方面表现良好,能够有效收敛到最短路径,提高路径规划的精度和稳定性。
理论
哈里斯鹰优化算法(HHO)是一种新型的智能优化算法,模拟哈里斯鹰在猎食时的搜索策略,分为探索和开发两个阶段。通过调整猎物与猎鹰间的距离,HHO算法动态调整个体位置,逐步逼近目标位置。应用于路径规划时,HHO通过在二维栅格中搜索最优路径,从而在保证避障的前提下找到最短路径。
实验结果
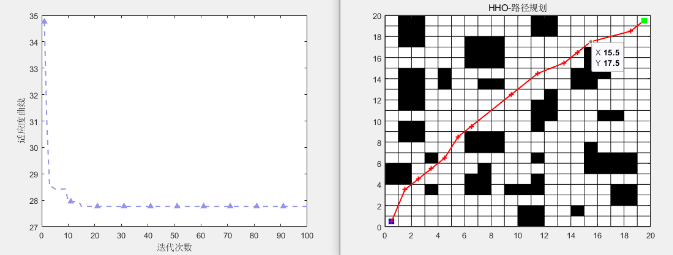
实验在20x20的二维栅格地图上进行了路径规划仿真:
-
适应度收敛曲线(见左图):展示了HHO在100次迭代中的适应度值变化。可以看到,算法在前期快速收敛,适应度值趋于稳定,表明算法有效收敛到最优路径。
-
路径规划结果(见右图):红色线条显示了从起点(蓝色方块)到终点(绿色方块)的规划路径。路径成功避开了黑色的障碍物区域,展示了HHO算法的避障能力和路径优化效果。
部分代码
% 初始化参数
gridSize = 20; % 栅格大小
start = [1, 1]; % 起点
goal = [15, 17]; % 终点
obstacles = createObstacles(gridSize); % 障碍物位置
% 哈里斯鹰算法初始化
numHawks = 30; % 鹰群数量
maxIter = 100; % 最大迭代次数
positions = initializePositions(numHawks, start, goal, obstacles);
% HHO路径规划过程
for iter = 1:maxIter
for hawk = 1:numHawks
% 计算当前鹰与目标的距离
direction = calculateDirection(positions(hawk, :), goal);
% 更新鹰的位置,避开障碍物
newPosition = updatePosition(positions(hawk, :), direction, obstacles, gridSize);
% 检查新位置是否更优
if isBetterPosition(newPosition, positions(hawk, :), goal)
positions(hawk, :) = newPosition;
end
end
% 记录当前迭代的最优适应度
bestFitness(iter) = evaluateFitness(positions, goal);
end
% 绘制收敛曲线
figure;
plot(bestFitness, 'b--^', 'LineWidth', 1.5);
xlabel('迭代次数');
ylabel('适应度值');
title('适应度收敛曲线');
% 绘制路径规划结果
figure;
plotGridPath(positions, start, goal, obstacles, gridSize);
title('HHO路径规划');
参考文献
❝
Heidari, A. A., & Mirjalili, S. (2019). Harris Hawks Optimization: Algorithm and Applications. Future Generation Computer Systems, 97, 849-872.
Yang, S., & Deb, S. (2020). Intelligent Optimization Algorithms for Path Planning. IEEE Transactions on Automation Science and Engineering, 17(2), 744-753.
Li, J., & Li, Q. (2021). Path Planning for Mobile Robots Using Novel Optimization Algorithms. Journal of Robotics and Autonomous Systems, 133, 103628.
(文章内容仅供参考,具体效果以图片为准)
