杨辉三角形 (蓝桥杯) JAVA
目录
- 题目描述:
- 暴力破解(四成):
- 二分法破解(满分):
题目描述:
下面的图形是著名的杨辉三角形:
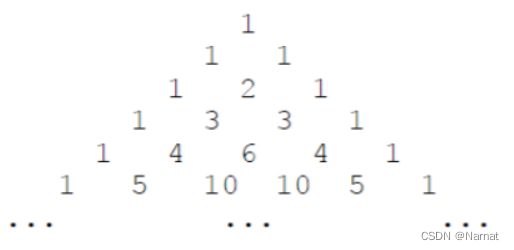
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
输入格式:
输入一个整数 N。
输出格式:
输出一个整数代表答案。
数据范围:
对于 20% 的评测用例,
1≤N≤10;
对于所有评测用例,1≤N≤10^9。
输入样例:
6
输出样例:
13
暴力破解(四成):
解题思路:
解决本难题的话,如果不是很了解杨辉三角的规律的话,可以用暴力混分。
想要暴力混分,得先明白杨辉三角形的最基本规的律:
1
1 1
1 2 1
1 3 3 1
1 2 6 4 1
1.每行首尾都是1
2.每行数字左右对称
3.第n行的数字有n列
4.每列上的元素值 = 上一行当前列元素值 + 上一行上一列元素值
了解上述基本规律就能将杨辉三角存入二维数组中,再输出。
对于本题我采用的是一维滚动数组来更新杨辉三角的值,因为一维数组最大可以分配 大概1 * 10^9左右的空间,能打印杨辉三角的最大宽度就很大了。而二维数组分配 10000*10000的空间就爆炸了。能打印杨辉三角的最大宽度就缩短了。
值得注意的是,更新一维数组的时候要从后往前更新,由于杨辉三角是具有对称性,所以不影响(从前往后更新的话,数据会被覆盖)。
用一维数组打印杨辉三角的代码如下:
import java.util.*;
public class Main{
public static long n = 0;
public static void main(String[] args){
long a[] = new long[1000000 + 1];
for(int i = 0; i <= 10; i ++) {
for(int j = i; j >= 0; j --) {
if(j == 0 || i == j) {
a[j] = 1L;
System.out.print(a[j] + " ");
continue;
}
a[j] = a[j] + a[j - 1];
System.out.print(a[j] + " ");
}
System.out.println();
}
}
}
用暴力破解本题,代码如下:
import java.util.*;
public class Main{
public static long n = 0;
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
n = sc.nextLong();
long a[] = new long[1000000 + 1];
long sum = 0;
out : for(int i = 0; i <= 1000000; i ++) {
for(int j = i; j >= 0; j --) {
if(j == 0 || i == j) a[j] = 1L;
else a[j] = a[j] + a[j - 1];
if(a[j] == n) {
sum ++;
System.out.println(sum);
break out;
}
sum ++;
}
}
}
}
上代码在官方平台能拿四成分数,虽然不多,但如果只会暴力的话这么些代码,得这些分也是可以接受的:

二分法破解(满分):
思路:
要使用二分法破解本题,就要对杨辉三角形,每个位置上的元素规律都有进一步的了解。
下面直接给出结论:

上图可知,左边与右边对称,所以只需要研究左边即可。
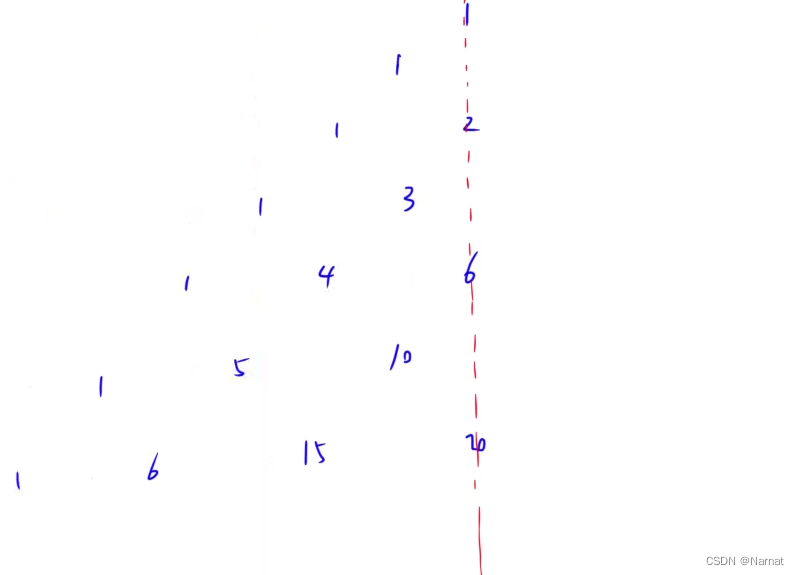
上述的一半可以直接用下方的排列组合式子表示:

加一些标注如下图:
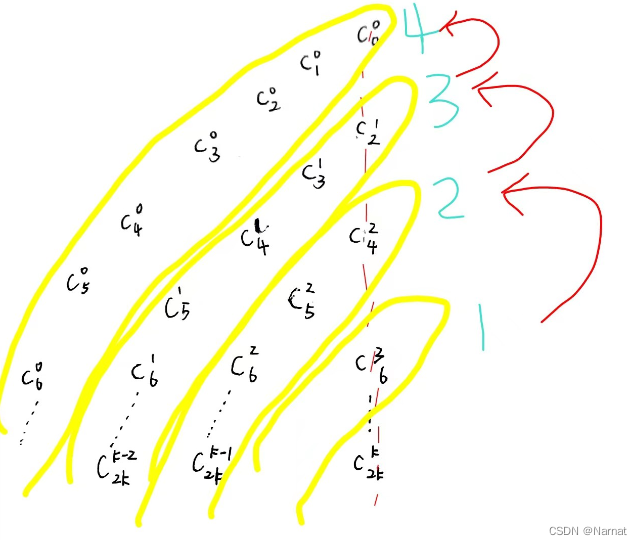
注意要求找到n第一次出现的位置:
很容易可以看到每一层 斜排 内的元素从上往下都是单调递增的,且越靠内扩张越快。所以靠内斜排 上的元素扩张的最快,所以能最快碰到第一个n。所以在二分查找的时候我们从内层往 外层 找(这样找到的 n 就是第一次出现的),由于杨辉三角扩散速度很快,所以 16 斜层 就可以包含10^9的数据。
如上图标记,我们从内往外,先 找 1 层,看是否有一个 C(r , k) = n 如果有的话我们直接退出,否者继续去找 2 层…直到找到一个C(r, k) = n 再通过r, k 找到这个数是第几次出现的(用N表示)。
这里直接给出结论:N = r *(r + 1) + k + 1
(上述公式只要知道:r, k 是从 0 开示的就不难推出N)
还需要注意的是本题用long变量储存数据,出现 long >> 1 + int 类型的式子是很容易让最终结果出错的。
例如:
public class text {
public static void main(String[] args) {
long a = 2L;
System.out.print(a >> 1 + 1);
}
}
输出:
修改方法有两种,正确代码:
public class text {
public static void main(String[] args) {
long a = 2L;
long b = 1L;
System.out.println((long)(a >> 1) + 1L);
System.out.print(a / 2 + 1);
}
}
输出:

理论成立本题完整代码如下:
import java.util.*;
public class Main{
public static int n = 0;
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
n = sc.nextInt();//别写成int n
for(int i = 16; i >= 0; i --) if(check(i)) break;
}
public static long C(long a, long b) {//求排列组合C(a,b)的值
long res = 1;//不要写成res = 0;
for(long i = a, j = 1; j <= b; j ++, i --) {
res = res * i / j;
if(res > n) return res;//大于n直接退出防止爆long
}
return res;
}
public static boolean check(int k) {
long L = 2 * k;//C(2*k, k) ~ C(N, k),这个区间内寻找一个C(r, k) = n
long R = n;//左右边界,C(1, n) = n,所以右边界最多是n
while(L <= R) {
long middle = (L + R) >> 1;//高效 除 2
long nt = C(middle, k);
if(nt > n) R = middle - 1;//大于查左边部分
else if(nt < n) L = middle + 1;
else {
System.out.print((middle *(middle + 1)) / 2 + k + 1);//输出结果,再退出
return true;
}
}
return false;
}
}

