论文精读：NC kagome FeGe 自旋声子耦合驱动CDW 实验与理论计算

Nat Commun 14, 6183 (2023). 

https://doi.org/10.1038/s41467-023-41957-5

摘要节选

自旋、电荷和晶格自由度之间的纠缠可以产生不寻常的宏观量子态，包括高温超导和量子反常霍尔效应。

最近，在kagome反铁磁体FeGe中观察到电荷密度波（CDW），表明可能存在缠结物理。一个突出的问题是磁关联是否是自发空间对称破缺序的基础。

在这里，利用弹性和高分辨率的非弹性x射线散射，我们观察到一个c轴超晶格矢量与kagome平面上的2 × 2 × 1 CDW矢量共存。最有趣的是，在磁性和CDW转变温度之间，声子动态结构因子显示出巨大的声子能量硬化和c轴波向量附近的声子线宽显着拓宽，两者都表明自旋声子耦合。

通过第一性原理和模型计算，我们证明了静态自旋极化和动态自旋激励都与声子相互交织，驱动FeGe中的空间对称性破缺

背景

kagome晶格的磁性和特征电子结构的结合，包括平带、Dirac-fermion和van Hove奇点，是实现相关和拓扑量子态的有效途径。

重要的兴趣集中在kagome超导体AV3Sb5 (A = K, Rb, Cs)费米能级附近的van Hove奇点触发级联时间和空间对称性破缺顺序上。

最近，在kagome磁体FeGe上发现了与AV3Sb5 (A = K, Rb, Cs)类似的电子结构在费米能级EF附近具有多个van Hove奇点。在A型反铁磁（A- AFM）相中发现电荷密度波（CDW），和包括异常霍尔效应和鲁棒边缘模式在内的相关物性。在CDW转变温度（TCDW）以下，静态自旋极化增强，表明自旋、电荷和晶格自由度之间存在密切关系。

关键问题仍有待解答。例如，虽然在相关的磁性体系中已经观察到CDW，例如铜的高TC超导体和自旋密度波系统，但远低于磁转变温度的CDW的出现是罕见的，这表明在FeGe中存在一种新的相关驱动的CDW机制。

在EF附近具有van Hove奇点是kagome金属研究中的重点关注，也迫切需要确定FeGe中CDW的几何形状及其与环路电流场景的可能联系。

本文使用先进的x射线散射和数值计算来解决这些基本问题。在FeGe的A-AFM波矢上发现了电荷超晶格峰，区分了FeGe和AV3Sb5的CDW几何形状，尽管它们具有相同的2 × 2 × 2超结构。最有趣的是，声子动力结构因子在TCDW上方的c轴CDW波向量附近显示出巨大的声子硬化和大的声子展宽效应。这些声子异常与电子-声子耦合系统中的声子软化形成鲜明对比，称为Kohn异常，以及在TCDW以下变硬的新振动模式。

结合密度泛函理论（DFT）和模型计算，FeGe中能量有利的2 × 2 × 2超结构主要涉及Kagome平面上的c轴晶格畸变，该畸变由强自旋声子相互作用稳定。

结果与讨论

FeGe为六边形结构，空间群为P6/mmm (No.191)。

它是由以Ge-1为中心的六边形铁原子组成的kagome晶格。这些kagome层沿着c轴堆叠，并被Ge-2的蜂窝层分开。

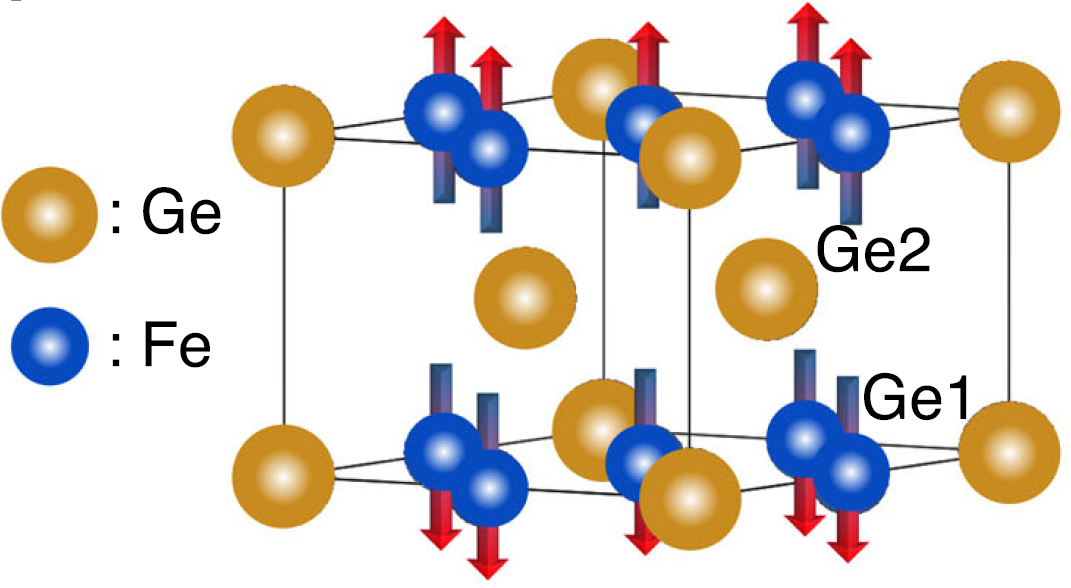
TN = 410 K以下，存在A-AFM，自旋力矩指向c轴。在TCDW ~ 110 K以下，观察到CDW伴随的反常霍尔效应和增强的自旋极化。

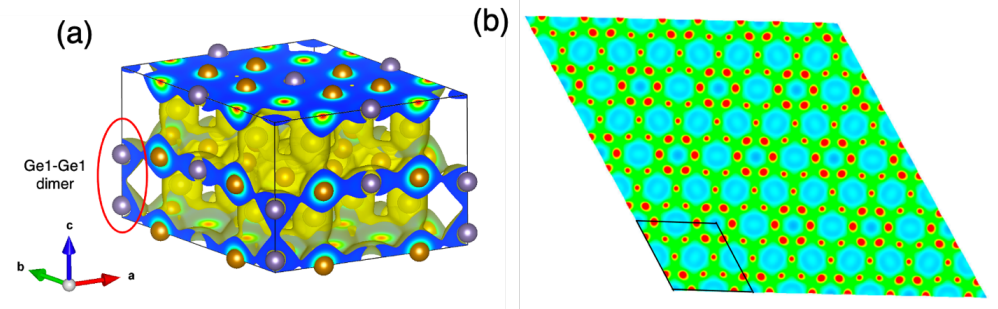
DFT计算的CDW基态电荷密度图。

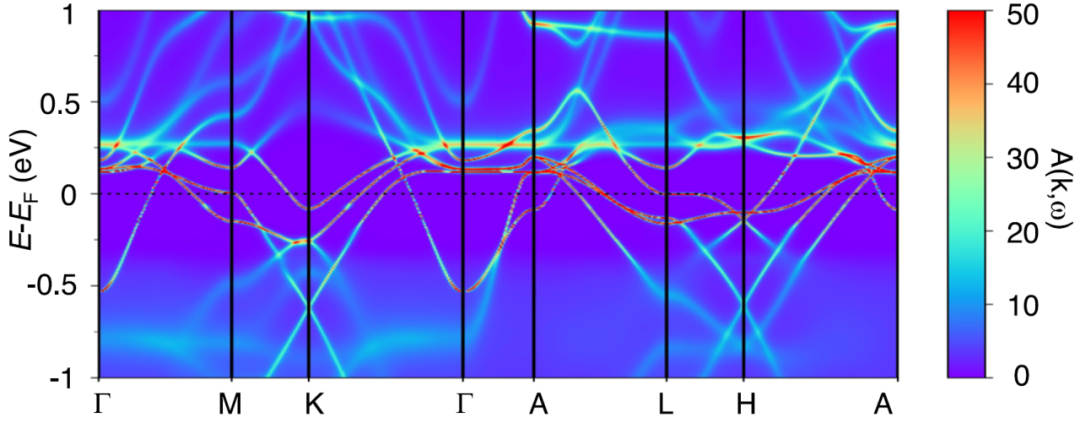
密度泛函理论加动态平均场理论（DFT + DMFT，U = 4.2 eV和JH = 0.88 eV的A-AFM相）计算的FeGe谱函数与角分辨光谱学（ARPES）研究一致，由于局域关联效应，M点的van Hove奇点被推到了费米能级。

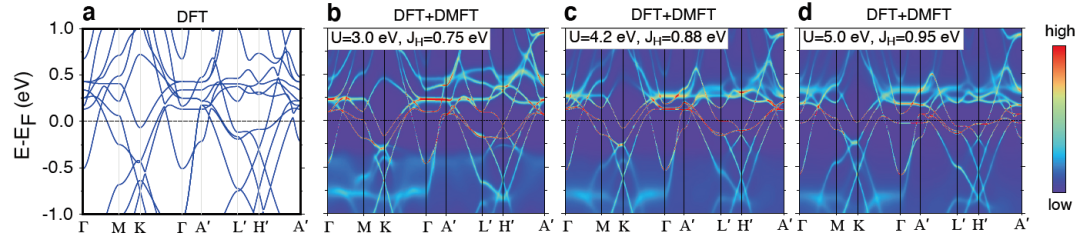
DFT和𝑈= 3𝑒𝑉，𝐽= 0.75𝑒𝑉；𝑈= 4.2𝑒𝑉,𝐽= 0.88𝑒𝑉和𝑈= 5𝑒𝑉,𝐽= 0.95𝑒𝑉的DMFT计算得到的能带结果。

非磁性体和表面（灰色六边形）布里渊区的高度对称点和方向。

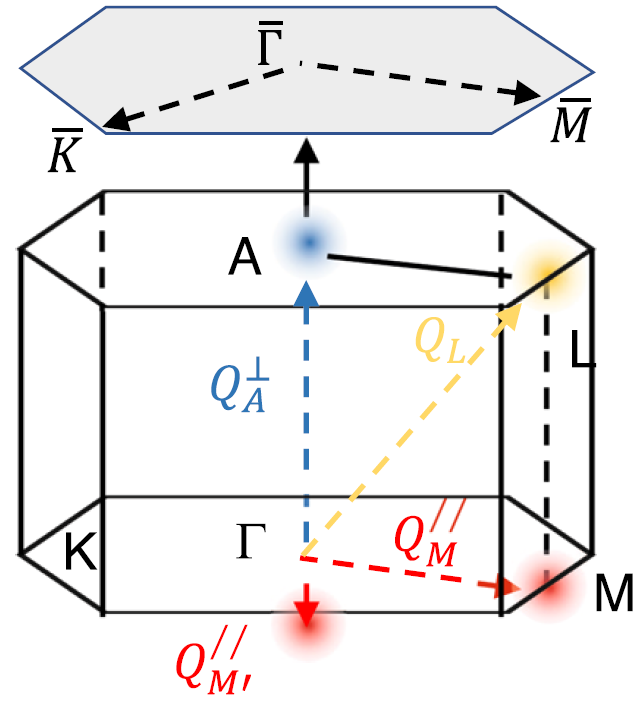
由于磁性单元胞沿Γ-A方向是非磁性单元胞的两倍，磁性布里渊区是沿Γ-A方向的非磁性布里渊区的一半。Q⊥A和Q∥M分别对应电荷二聚体和van Hove奇点嵌套波向量。QL自然地被描述为Q⊥A和Q∥M。

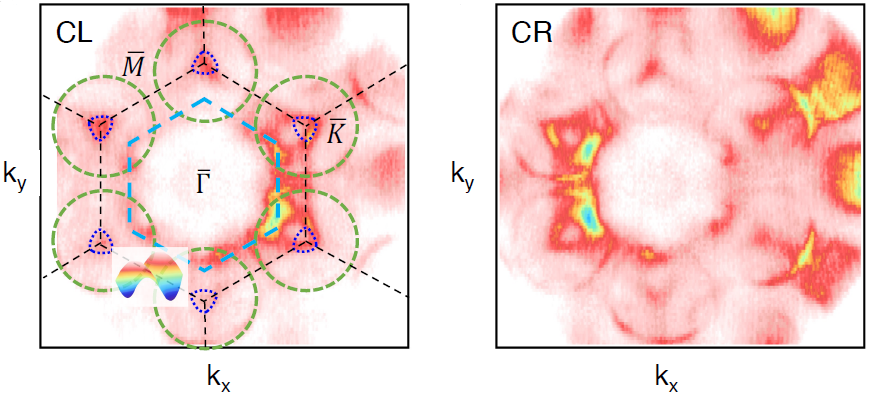
左旋（CL）和左旋（CR）入射光子（100 eV）偏振测量的FeGe的费米面。

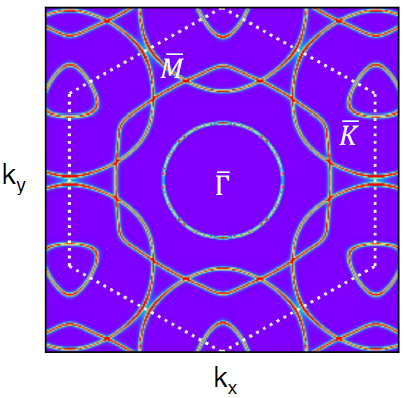
在U=4.2 eV和JH=0.88 eV下，DFT+DMFT计算的a型AFM相kz=0处的费米表面与实验数据吻合较好

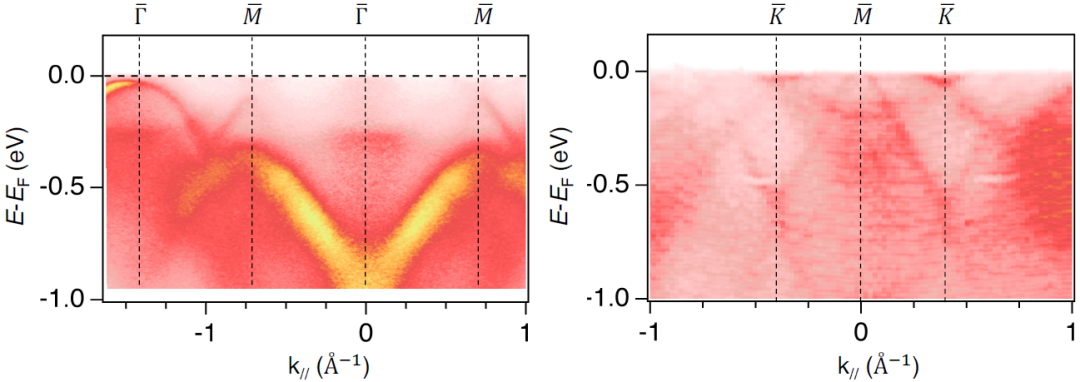
沿高对称性𝛤-𝑀和𝐾-𝑀方向的ARPES强度图。与先前的研究一致，𝑀点的范霍夫奇点略高于费米能级。整个费米表面拓扑结构和能带结构与FeSn3非常相似

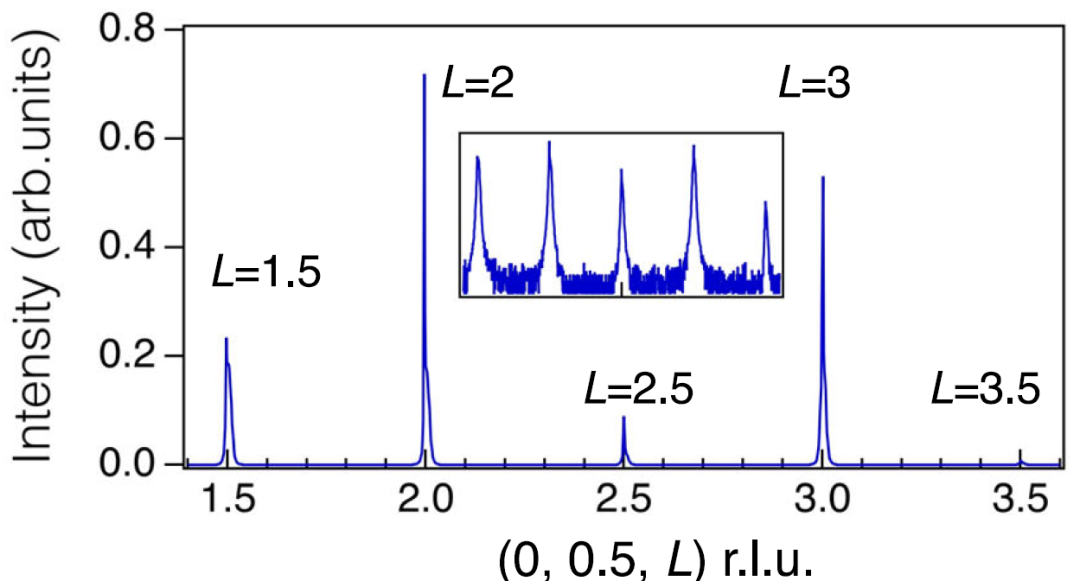
T = 10 K时沿高对称方向的x射线衍射扫描图。

在Q∥M （H = 0.5， K， L=整数）和QL （H = 0.5, K L=整数+0.5）处观察到CDW超晶格峰，与AV3Sb5相同。但在Q⊥A = (0,0,2.5)方向发现的峰在AV3Sb5 中不存在。

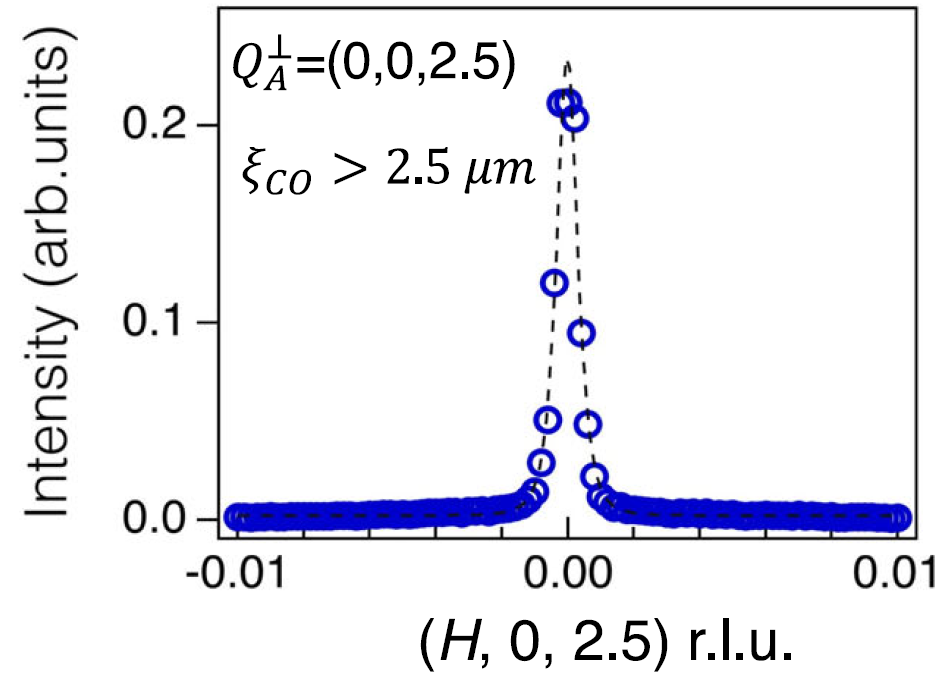
这种新的超晶格峰很窄，在倒易晶格单元中半宽半最大值（HWHM）约为0.001，并且沿晶体c轴的单元胞加倍。

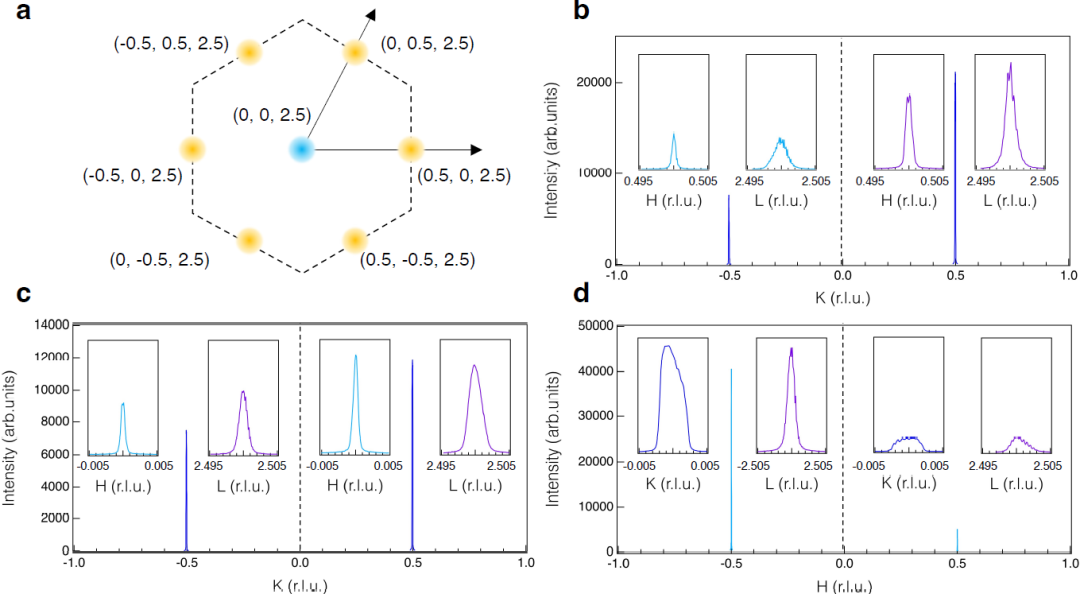
基于动量空间L=2.5平面上的CDW矢量Q =(0.5, -0.5, 2.5)，(-0.5,0.5,2.5)，0.5, 0,2.5)，（-0.5,0,2.5），(0, -0.5, 2.5)和（0,0.5,2.5）的HKL扫描 。

由于Q⊥A = （0,0， L=半整数）与A型AFM峰重叠，因此有必要证明Q⊥A处观测到的峰不是x射线散射磁截面引起的。

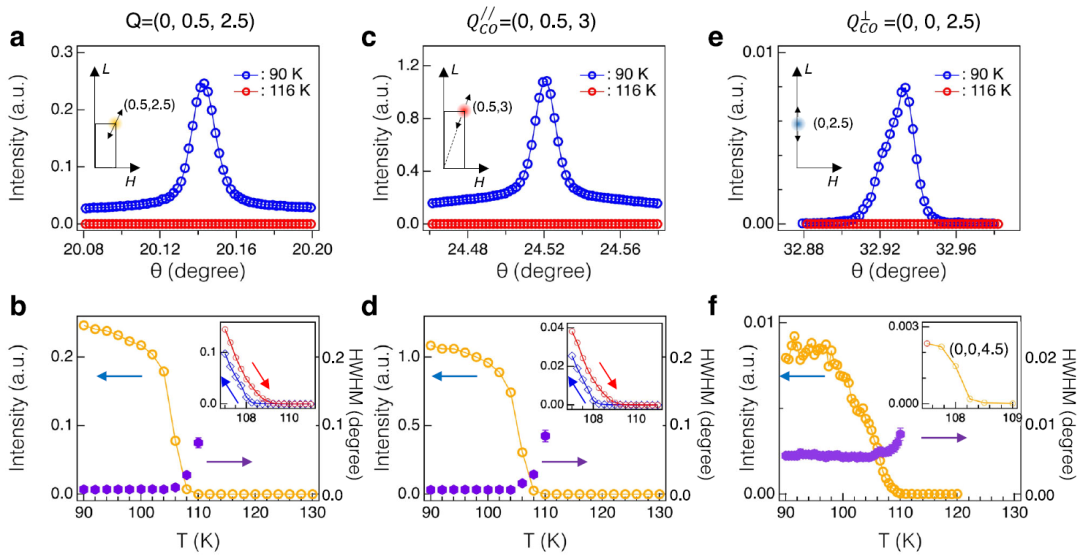
基于QL = (0,0.5, 2.5)， Q∥M =(0,0.5, 3)和Q⊥A=(0,0,2.5)和（0,0,4.5）的温度相关超晶格峰，在TCDW （90 K）以下和（116 K）以上的θ - 2θ扫描以及穿过TCDW与温度相关的峰强度和峰宽度。APS, hν=23.71 keV。

四种波矢量的起始温度相同，证明了Q⊥A峰对应于沿c轴的电荷超晶格。由于Q = (0,0,l)处的x射线散射振幅探测了沿c轴的晶格畸变，因此Q⊥A处的超晶格峰在TCDW处相邻FeGe层之间沿c轴建立了面外的晶格畸变。b、d的插图显示了TCDW附近QL和Q∥M处的迟滞扫描。迟滞温度（ΔT ~ 0.5 K）较小，表明TCDW处的转变为弱一级转变。

没有在Q⊥A处观察到温度相关的滞后，可能是由于其在TCDW附近的峰值强度相对较弱或滞后温度ΔT更小。考虑到FeGe中同时存在Q⊥A和Q∥M ，应将QL处的2 × 2 × 2上部结构峰视为Q⊥A和三个等效的Q∥M 的叠加。

Q⊥A 峰的一个重要结果是它区分了FeGe和AV3Sb5中的2 × 2 × 2电荷调制，指出了这两种kagome金属中cdw的不同电子和结构起源。

在A-AFM峰之上的Q⊥A 电荷超晶格峰的观测自然指向FeGe中的自旋声子相互作用。因此，使用meV分辨率非弹性x射线散射（IXS）来确定声子动力结构因子S（Q, ω）。

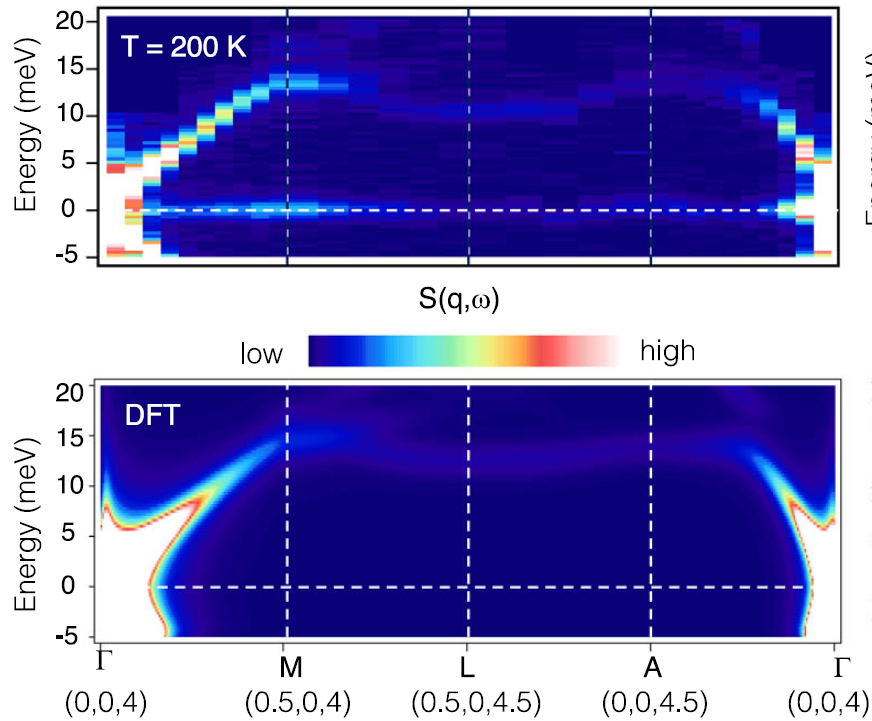
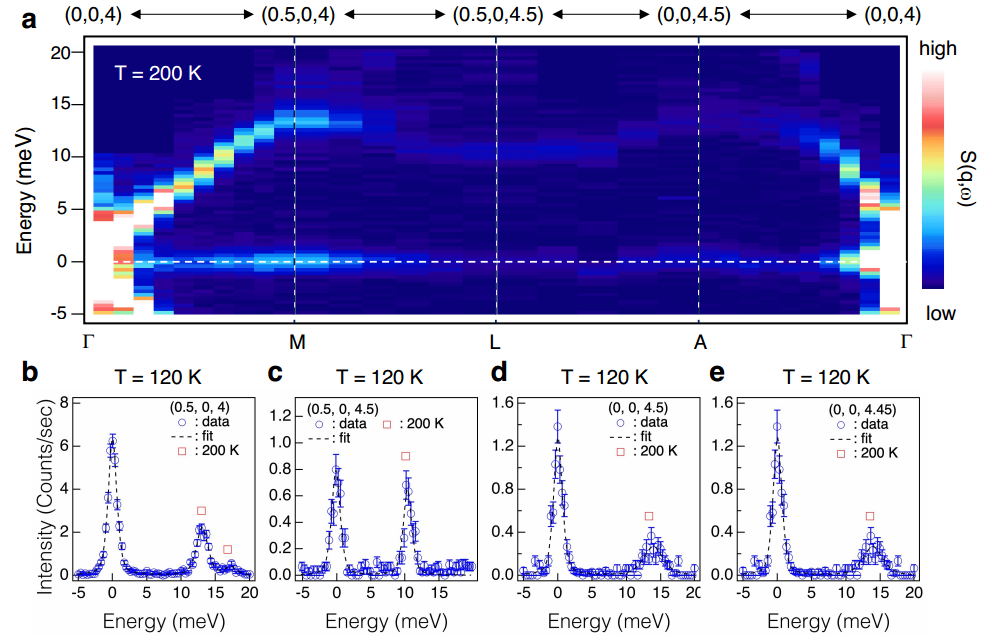
在200k下沿Γ(0,0,4)-M(0.5, 0,4)-L(0.5, 0,4.5)-A(0,0,4.5)-Γ（0,0,4）方向的实验和DFT计算的S（Q, ω）。

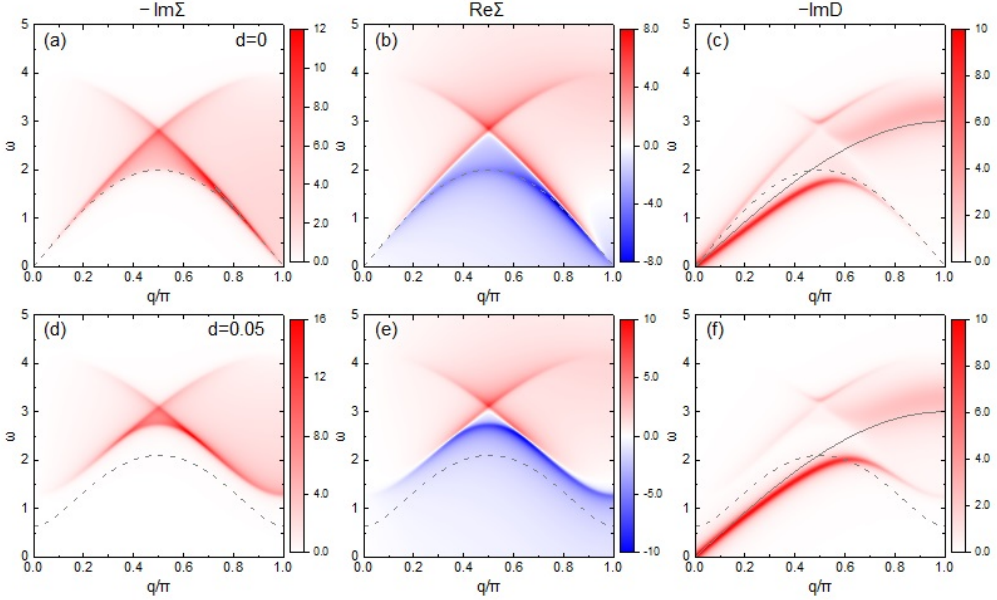
在声子色散和强度分布等方面，IXS与DFT的总体一致性较好。Q⊥A 附近的声子峰宽度异常宽，表明准粒子相互作用

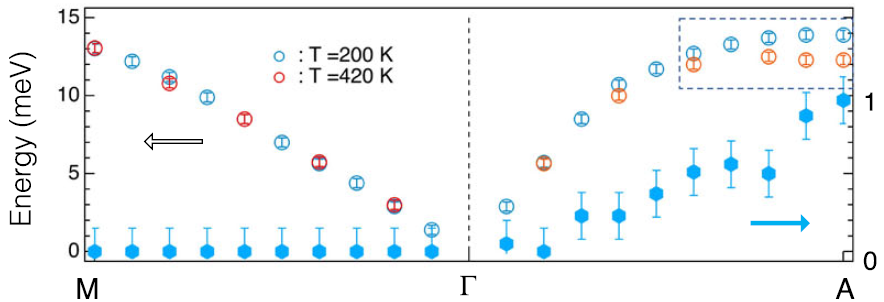
沿M-Γ-A方向200 K和420 K声子带色散，虚线矩形突出了A点附近与温度相关的声子能量重整化。。

声子在A点的能量从420 K到200 K增加了10%以上，同时声子线宽变宽。

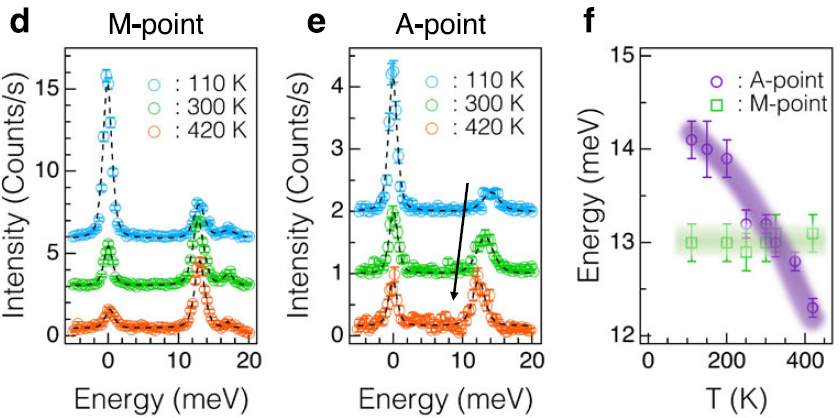
在M和A点的温度依赖的IXS光谱。虚线为实验数据的拟合。

M点的声子峰在实验误差范围内保持温度无关，而A点的声子模式在420到110 K之间表现出14%的巨大硬化。

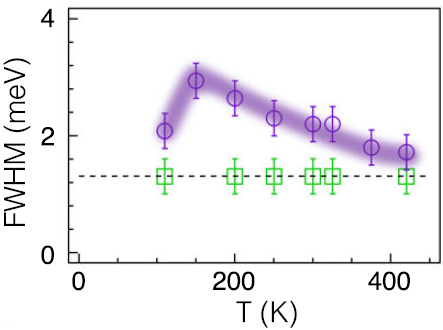
A点和M点与温度有关的声子宽度。拟合声子在A点的峰宽较宽，甚至高于TN，半最大全宽（FWHM）约为2 meV。在温度达到TCDW前宽度不断增加。在T = 150 K时，拟合的FWHM为~ 3 meV（对应于反卷积后的~2 meV本征声子宽度），产生约7%的衰减比例。

M点和L点声子峰宽在整个温度范围内分辨率有限，这与M点和L点不存在纵向和横向声子能量异常相一致。

在FeGe中观测到的声子在TCDW以上的硬化和加宽与电子-声子耦合CDW系统中的Kohn异常和TCDW以下的突现振幅模式有着根本的不同。这些声子异常如动态自旋声子耦合图所示。

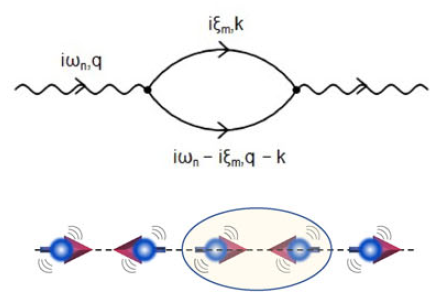
二阶费曼图描述了一个具有能量ωn和动量q的声子，它散射成两个具有（ξm, k）和（ωn-ξm, q-k）的磁振子。

这种动态自旋声子相互作用产生了强大的声子自能效应，包括声子能量硬化和声子线宽在a点附近展宽，这与实验观察一致。

有趣的是，在Kondo绝缘体FeSi和自旋- peierls化合物CuGeO3中观察到类似的声子异常，支持自旋-声子耦合系统中普遍存在的声子硬化和加宽。

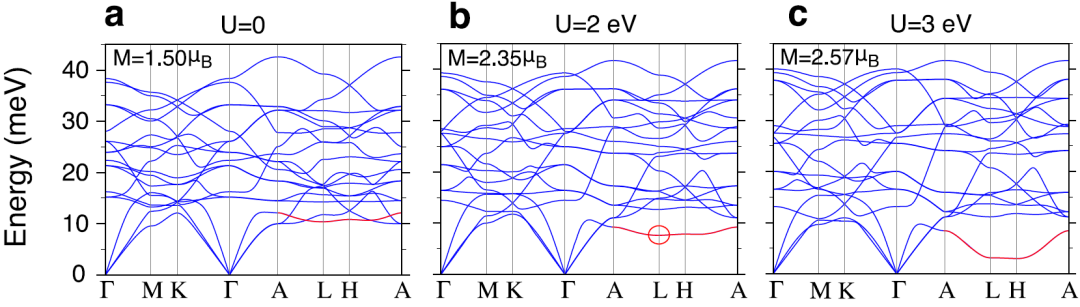
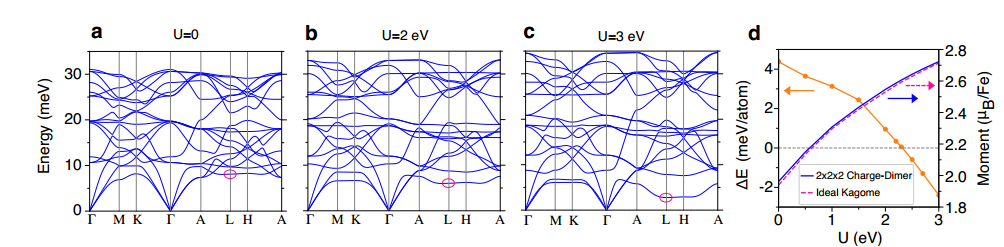
FeGe在A-AFM相随Hubbard U的增加的声子谱。当U < 2 eV时，随着U的增加，能量最小的L点声子模式的变化最为显著的。

这一结果表明，较强的电子相关和自旋极化倾向于诱导FeGe中的晶格不稳定性。

这种模式对应的原子振动主要由相邻Fe-Ge kagome层之间的面外c轴晶格畸变组成，与实验观察到的Q⊥A超晶格峰一致。

为了理解2 × 2 × 2超结构的性质，我们取实验观测到的声子模式在三个等效L点处的等相位和振幅叠加。

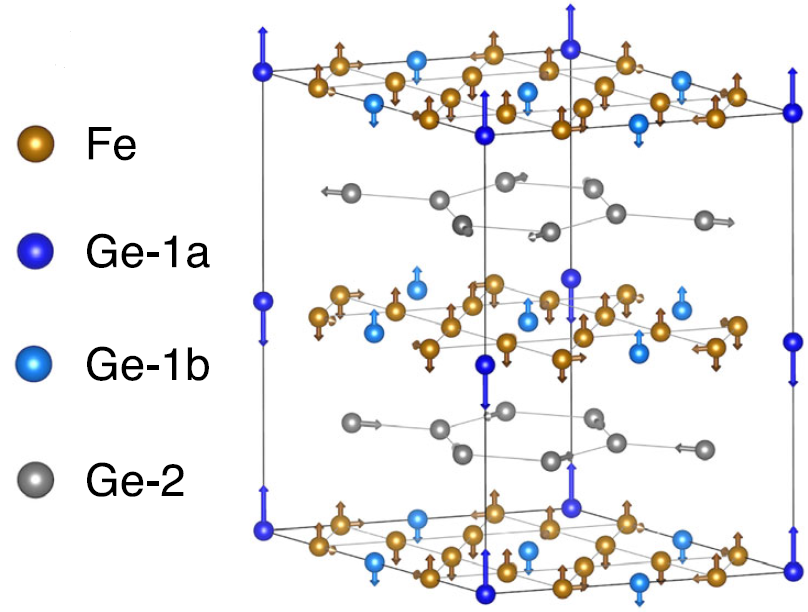
箭头指向铁和锗原子的运动方向。。在kagome层中，Fe和Ge原子沿c轴向平面外移动。Ge-1原子分为面外的Ge-1a（蓝色）和Ge-1b（浅蓝色）基团，其中Ge-la的原子运动比Ge-1b大得多，沿c轴形成Ge-1二聚体。Ge−2原子的蜂窝状层（灰色）表现出面内kekul型畸变

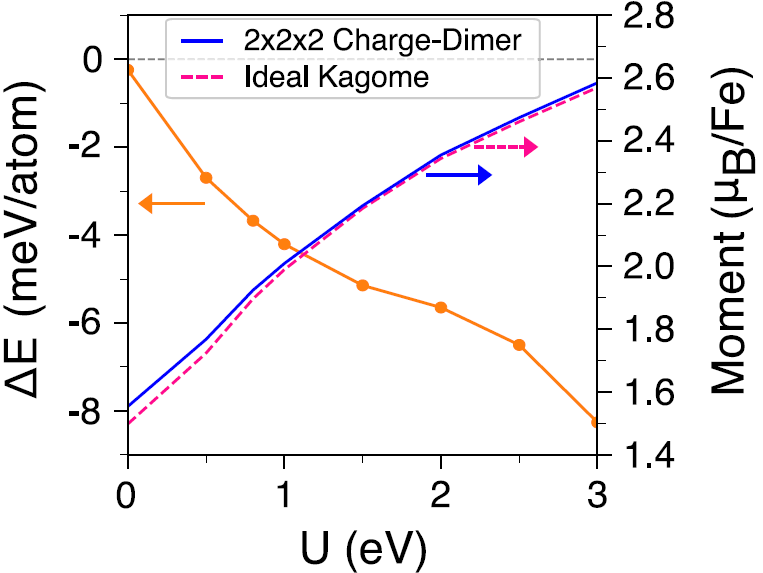
从这个P6/mmm空间群的2 × 2 × 2超胞开始弛豫，超胞与理想kagome相ΔE = EChargeDimer - EKagome之间的能量差如图，该能量差随U的增加而减小。2 × 2 × 2的超胞在U= 0时已经是一个能量有利的相，并且在静力矩中随着U的增加而强化。

这些结果表明，静态自旋极化的大小对于稳定Kagome平面上具有大c轴晶格畸变的2 × 2 × 2超胞是重要的。

此外在U= 0 ~ 3 eV时，有序磁矩进一步增强了0.01 ~ 0.05 μB/Fe，这与之前的中子散射研究结果一致。

需要指出的是，实验确定的静态自旋磁矩与U= 0时的DFT + U计算结果更为一致，因此，静态磁矩在高温下引起的声子软化效应可以忽略不计，主导声子异常被认为是动态磁子-声子耦合引起。

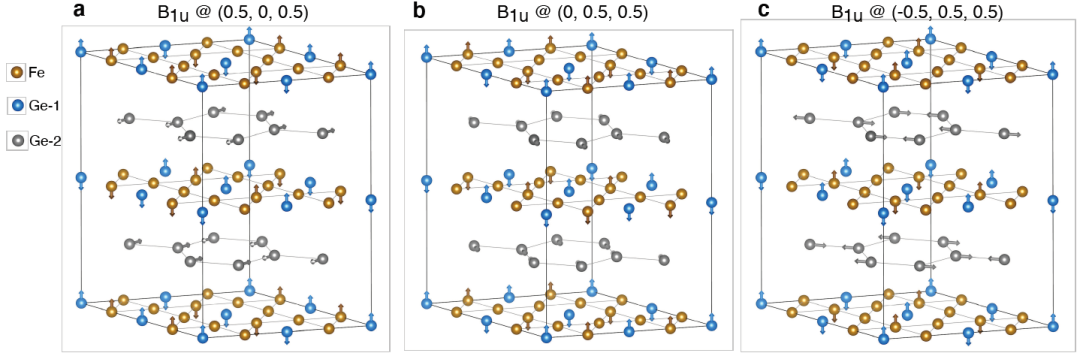
三个等效L点处B1u声子模式的原子振动。

讨论1：FeSn对比

FeSn中自旋极化诱导2×2×2的超胞结构声子谱计算

FeSn具有TN~365K的A型AFM。

与FeGe相似，计算得到的FeSn声子谱也显示出随着U的增加，L点上的变量值和声子值都发生了剧烈的变化，用红色圆圈表示。局部“电荷二聚化”的2 × 2 × 2超胞与理想Kagome相之间的能量差。

与FeGe相比，电荷二聚体的超胞只有在非常大的U （>2.4 eV）时才具有较低的能量，这表明FeGe倾向于具有理想Kagome结构的基态。

这些化合物之间存在差异的可能原因是FeSn的c轴晶格参数比FeGe的c轴晶格参数大10%左右，这使得FeSn沿着c轴的二聚化是不利的。事实上，当U<1 eV时，FeGe的自旋极化增强约为FeSn的两倍。

讨论2：两个磁振子激发的声子寿命

现在讨论自旋-声子耦合如何诱导声子寿命效应。

纵向晶格位移改变相邻自旋之间的交换耦合。在反铁磁体中，这样的离子位移可以激发两个磁振子，比如说，一个是右螺旋，另一个是左螺旋，因此总自旋保持不变。假设一个动量𝑞和能量𝜔q的声子衰变成两个磁振子，一个动量𝑘和能量𝜀k，另一个动量𝑘'和能量𝜀𝑘'。

由于能量和动量守恒，必须满足

和

这导致了

这意味着声子衰变为两个磁振子的能量最低𝜔q。

此外，由于纵向声子模式在小动量𝑞下由晶格位置的几乎均匀位移组成，因此不会改变交换耦合。为了与磁振子耦合，纵向声子需要有很大的动量。

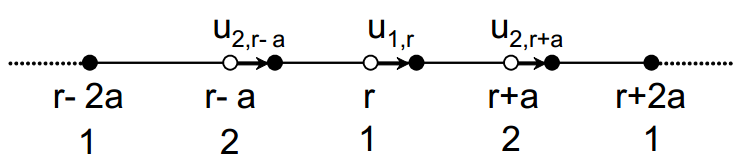
磁性离子位移由𝑢。晶格常数𝑎。

这种位移改变了相邻自旋之间的交换耦合并激发了磁振子。

为了证明纵向声子和磁振子之间的耦合，这里我们考虑一维反铁磁海森堡链，它可以表明FeGe沿z方向的磁性和声子的基本物理。

假设具有两个磁亚晶格1和2的Neel有序，这种耦合可以通过以下方式建模：

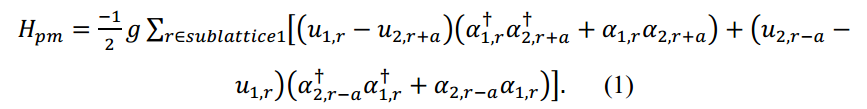
𝑔是声子-磁振子耦合常数，表示原子位移对交换的调制。𝑢𝑙𝑟是子晶格𝑙在𝑟位置上的晶格位置的纵向位移。𝛼是子晶格𝑙位置上的磁振子湮灭/产生算子。

为简单起见，我们只考虑磁振子湮灭和产生算子的傅里叶变换为

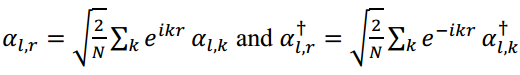
将磁振子哈密顿量表示为

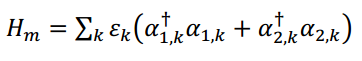
𝜀k为磁振子色散，𝐽为交换常数，将作为下面的能量单位，𝑑表示单离子沿z轴的各向异性。

两个磁振子模式𝑙= 1和𝑙= 2具有相反的旋度。

引入晶格位移场的傅里叶变换

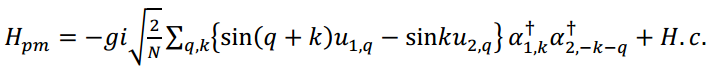
动量的总和𝑞和𝑘在磁布里渊区[−𝜋⁄2,𝜋⁄2]是有限的，

分别分离声光模式𝑢aq和𝑢oq之间的位移场。

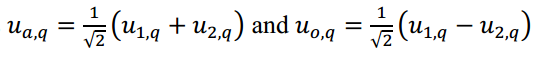
得到

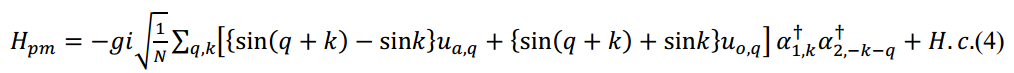
将位移场二次量子化

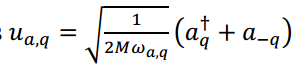
声子-磁振子耦合表示

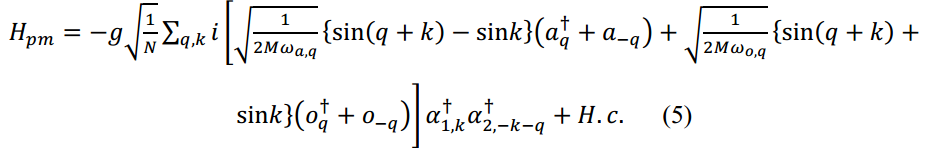
𝜔aq和𝜔oq是由给出的声子和光学声子的色散

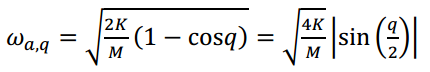
扩展动量𝑞空间[−𝜋,𝜋]上

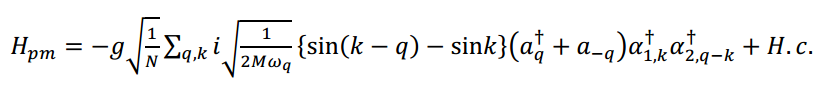
利用Matsubara式，通过二阶微扰计算得到声子的自能。

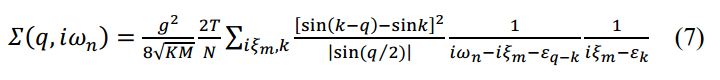
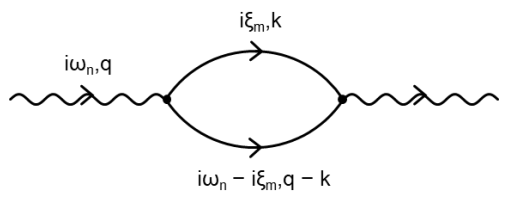
声子自能的二阶费曼图

声子在零温度下的延迟自能

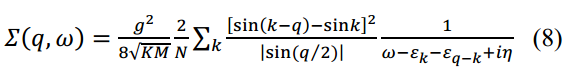
纵向声子在𝑞→0处声子-磁振子耦合应该消失。

声子的格林函数为

声子自能和格林函数的数值结果。

方法

样品制备和表征

化学气相输运法（CVTC）制备FeGe单晶。碘为运输剂。温度：600°C（源）550°C（汇）。12day。

典型尺寸1.5 × 1.5 × 3 mm3

弹性x射线散射

美国阿贡国家实验室（ANL）先进光子源（APS）的4ID-D光束线上进行了单晶弹性x射线衍射。

入射光子能量11 keV，略低于Ge K-edge，以减少荧光背景。x射线的高次谐波通过硅反射镜和Si（111）单色器的失谐被抑制。衍射测量采用垂直散射平面几何和水平偏振（σ） X射线。入射强度由He填充的离子室监测，而衍射用一个能量分辨率约为200 eV的Si漂移能量色散探测器收集。样品温度由He闭合循环低温恒温器控制，并使x射线从（001）表面散射。

meV分辨率非弹性x射线散射

实验在APS， ANL40的30-ID-C （HERIX）束流线上进行。入射能量Ei = 23.7 keV （λ = 0.5226 Å）的高单色x射线束聚焦在样品上，光束截面为~ 35 × 15 μm2（水平×垂直）。HERIX光谱仪的总能量分辨率为ΔE ~ 1.5 meV（最大一半的全宽度）。测量是在反射几何中进行的。在这种几何结构下，IXS主要对沿晶体c轴的晶格畸变敏感。这种几何结构选择性地增强了DFT计算中预测的不稳定声子模式。在恒定动量传递Q下，能量扫描的典型计数时间为每点120 ~ 240秒，在室温下，H、K、L定义为六边形结构，a = b = 4.97 Å， c = 4.04 Å。

曲线拟合

总能量分辨率ΔE = 1.5 meV通过拟合弹性峰到伪pseudo-voigt函数来校准：

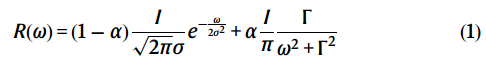
其中能量分辨率是FWHM。

IXS直接探测声子动态结构因子S（Q，ω）。立体角dΩ和带宽dΩ的IXS截面可表示为：

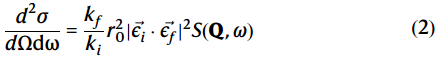
其中k和λ表示散射矢量和x射线偏振，I和f表示初始和最终状态。r0是电子的经典半径。在一个典型的测量中，能量传递ω远小于入射光子能量（23.71 keV）。
因此

S（Q， ω）与动态磁化率的虚部通过涨落耗散定理关系式

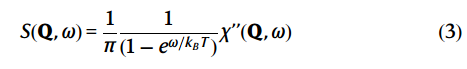
其中χ’‘（Q，ω）可以用具有反对称洛伦兹线形的阻尼谐振子形式来描述：

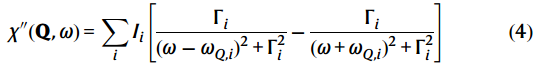
这里i表示不同声子的峰值

利用方程拟合恒定动量传递Q下的IXS谱，可以提取声子峰。(3)和(4).由于实验分辨率有限，IXS强度是S（Q， ω）与仪器分辨率函数R（ω）的卷积：

这里的R（ω）是通过弹性峰的拟合来确定的。

ARPES实验

ARPES实验是在单晶FeGe上进行的。样品在大于5 × 10−11 torr的真空条件下原位切割。实验在NSLS-II的21-ID-1波束线进行。采用同步加速器光源和ScientaOmicron DA30电子分析仪进行测量。ARPES测量的总能量分辨率约为15 meV。在整个实验过程中，样品阶段保持在T = 30k。

DFT + U计算

VASP，GGA-PBE，LDAUTYPE = 2。

使用FeGe实验晶格参数。

声子计算基于A型AFM相，具有2 × 2 × 1超胞（相对于AFM胞），DFPT。Phonopy 。

CDW 从2 × 2 × 2结构弛豫。0.001 eV/Å。Γ-centered 8 × 8 × 10 k点，ECUT500 eV。其他晶格1 × 2 × 2、√3×√3×2和√5x√ 5x2。所有这些都产生了比2 × 2 × 2结构和原始理想Kagome结构更高的基态能量。

DFT + DMFT计算

Wien2k ，DFT+DMFT代码。

在A型AFM自洽。杂化能窗口费米能级−10 eV到10 eV之间。

将Fe位上的5个三维轨道都看作是关联轨道，并采用伊辛形式的局域库仑相互作用哈密顿量，并结合不同的HubbardU和Hund耦合JH。

我们使用连续时间量子蒙特卡罗作为杂质求解器和haule的“精确”双重计数方案。为了计算谱函数，采用最大熵解析延拓法得到了电子在实频率上的自能。由于Fe-3d轨道的荷电性强度很小，很少会改变电子相关，因此荷电性不包括在DFT + DMFT计算中。所有的计算都在T = 80k时进行。

电子-声子与自旋声子驱动CDW

简化的1D Heisenberg模型：

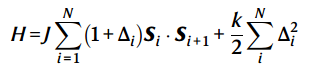
这里J是反铁磁交换能，Si是局部自旋。Δi = （-1）iδ， δ≥0，为连接位点i和i + 1的键处的晶格畸变，k为弹性常数。如果第一磁项的能量增益大于第二弹性项的能量损失，则CDW在能量上是有利的。