当前位置：首页 > article >正文

【leetcode练习·二叉树】用「分解问题」思维解题 I

article 2024/11/13 8:38:13

本文参考labuladong算法笔记[【强化练习】用「分解问题」思维解题 I | labuladong 的算法笔记]

105. 从前序与中序遍历序列构造二叉树 | 力扣 | LeetCode |

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

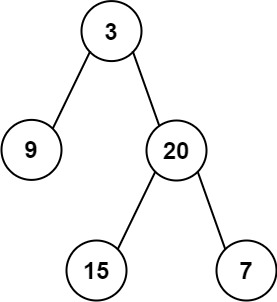
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

基本思路

构造二叉树，第一件事一定是找根节点，然后想办法构造左右子树。

二叉树的前序和中序遍历结果的特点如下：

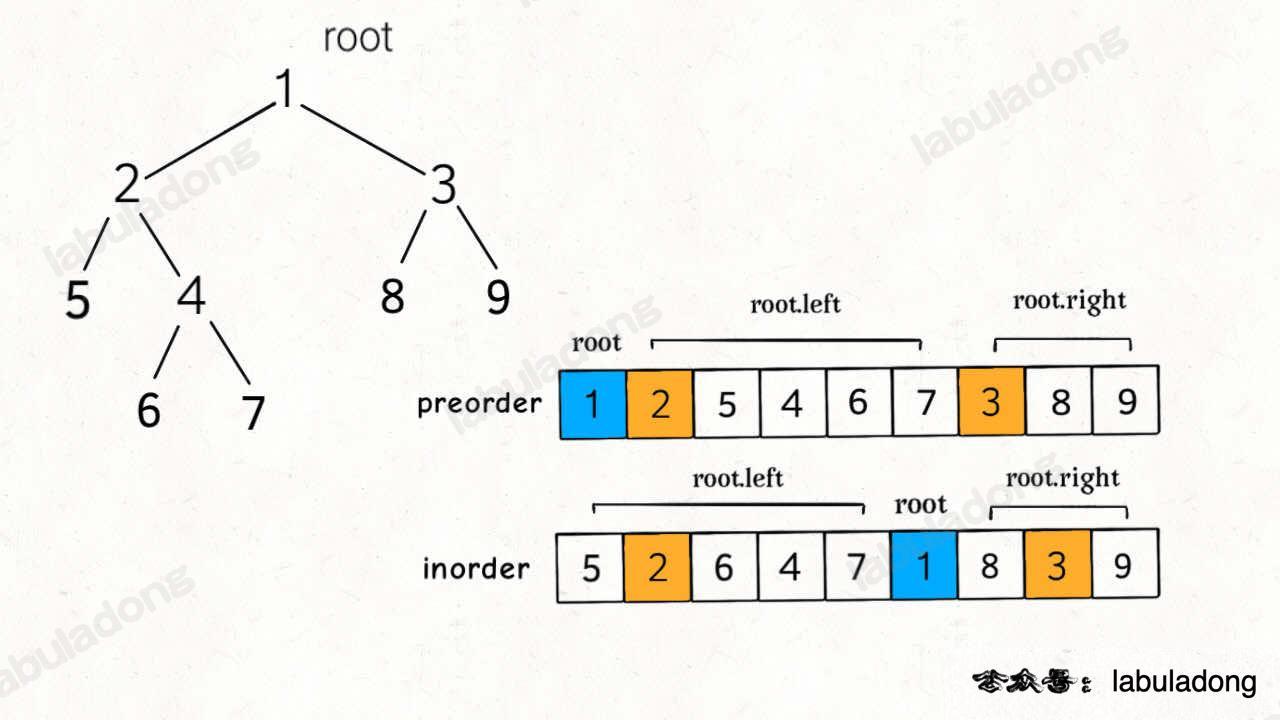
前序遍历结果第一个就是根节点的值，然后再根据中序遍历结果确定左右子树的节点。

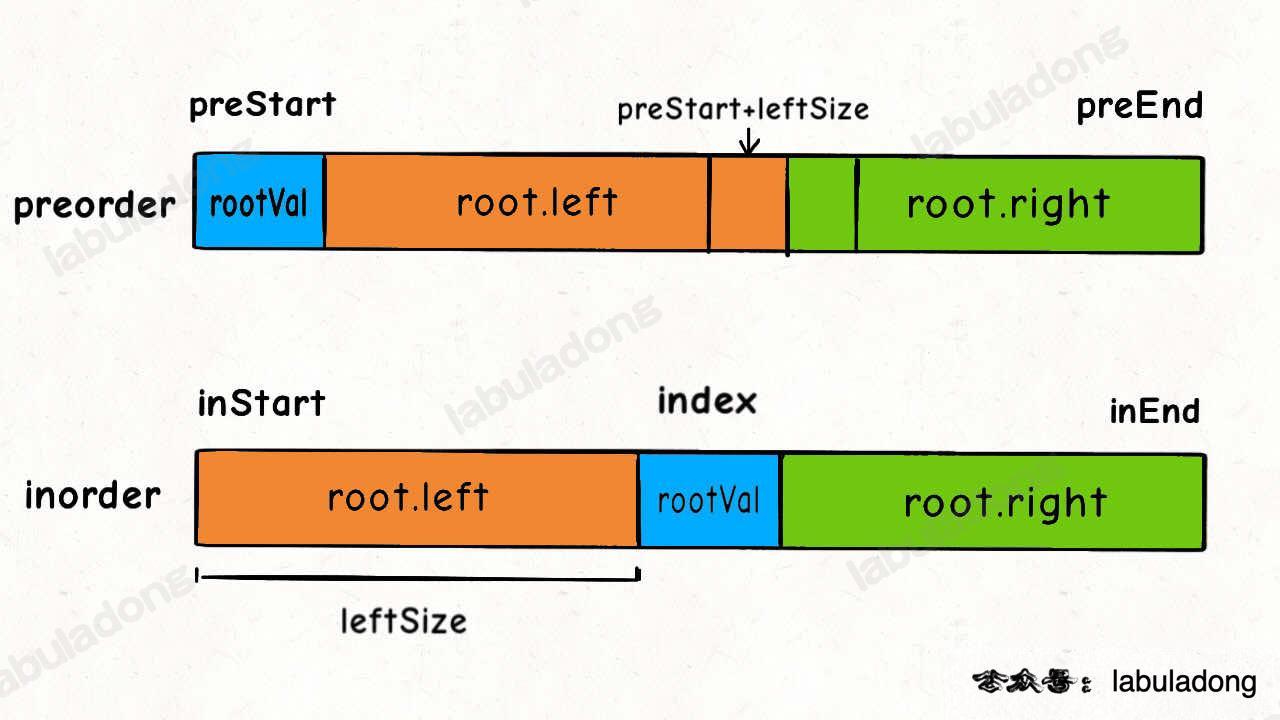
结合这个图看代码辅助理解。

详细题解

class Solution:
    # 存储 inorder 中值到索引的映射
    def __init__(self):
        self.valToIndex = {}

    def buildTree(self, preorder, inorder):
        for i in range(len(inorder)):
            self.valToIndex[inorder[i]] = i
        return self.build(preorder, 0, len(preorder) - 1,
                          inorder, 0, len(inorder) - 1)

    # 定义：中序遍历数组为 inorder[inStart..inEnd]，
    # 后序遍历数组为 postorder[postStart..postEnd]，
    # build 函数构造这个二叉树并返回该二叉树的根节点
    def build(self, preorder, preStart, preEnd, inorder, inStart, inEnd):
        if preStart > preEnd:
            return None

        # root 节点对应的值就是前序遍历数组的第一个元素
        rootVal = preorder[preStart]
        # rootVal 在中序遍历数组中的索引
        index = self.valToIndex[rootVal]

        leftSize = index - inStart

        # 先构造出当前根节点
        root = TreeNode(rootVal)

        # 递归构造左右子树
        root.left = self.build(preorder, preStart + 1, preStart + leftSize,
                               inorder, inStart, index - 1)

        root.right = self.build(preorder, preStart + leftSize + 1, preEnd,
                                inorder, index + 1, inEnd)
        return root

106. 从中序与后序遍历序列构造二叉树 | 力扣 | LeetCode |

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由不同的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

基本思路

构造二叉树，第一件事一定是找根节点，然后想办法构造左右子树。

二叉树的后序和中序遍历结果的特点如下：

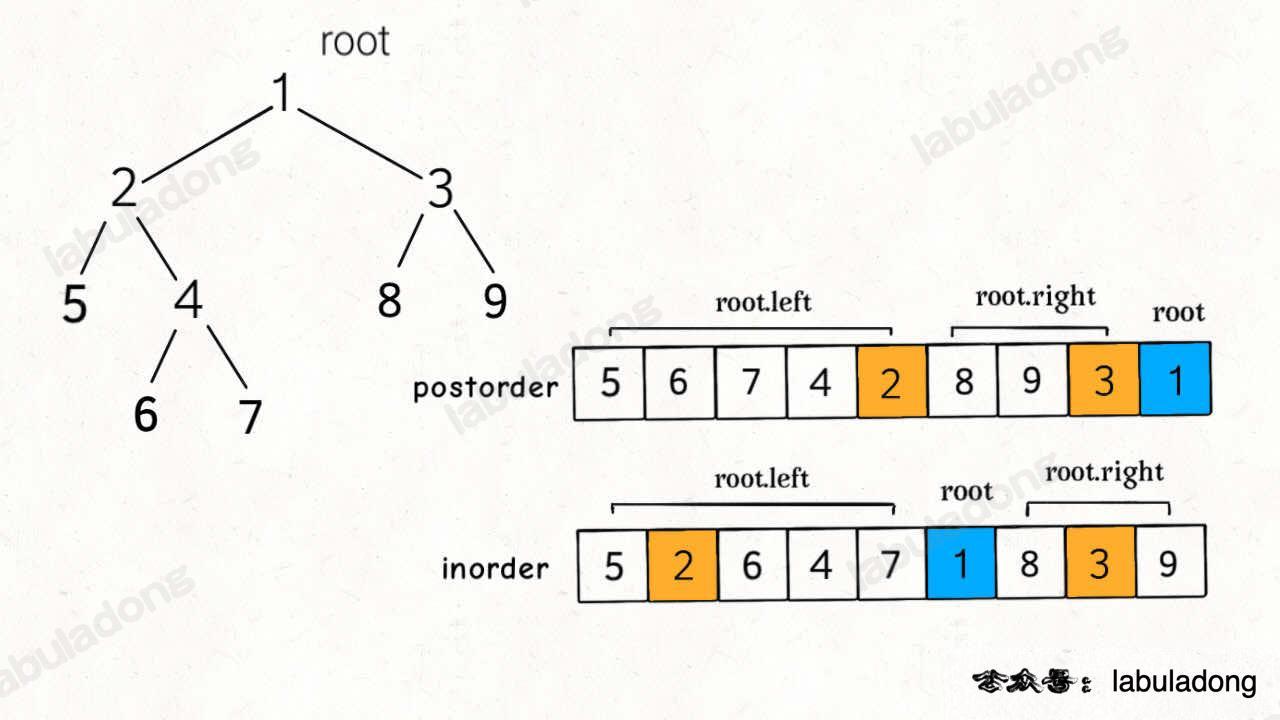
后序遍历结果最后一个就是根节点的值，然后再根据中序遍历结果确定左右子树的节点。

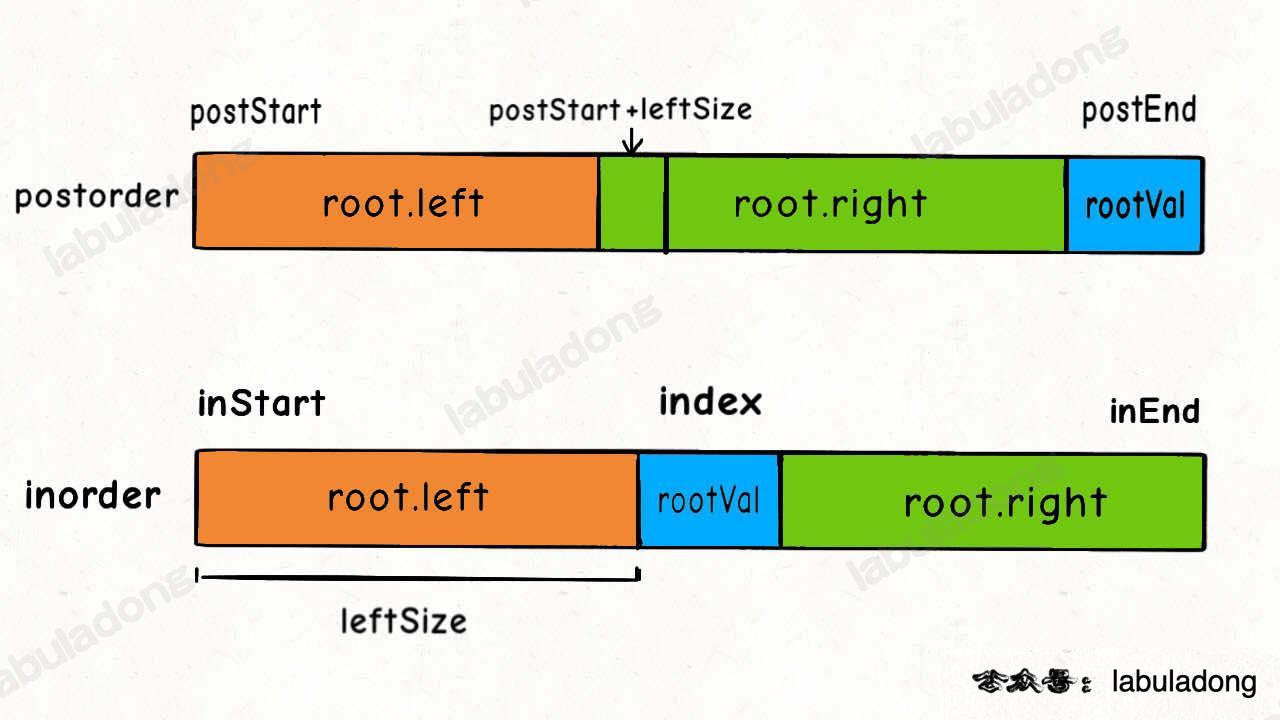
结合这个图看代码辅助理解。

详细题解

class Solution:
    # 存储 inorder 中值到索引的映射
    val_to_index = {}

    def buildTree(self, inorder, postorder):
        for i in range(len(inorder)):
            self.val_to_index[inorder[i]] = i
        return self.build(inorder, 0, len(inorder) - 1,
                          postorder, 0, len(postorder) - 1)

    """
    定义：
    中序遍历数组为 inorder[inStart..inEnd]，
    后序遍历数组为 postorder[postStart..postEnd]，
    构造这个二叉树并返回该二叉树的根节点
    """
    def build(self, inorder, in_start, in_end,
              postorder, post_start, post_end):

        if in_start > in_end:
            return None
        # root 节点对应的值就是后序遍历数组的最后一个元素
        root_val = postorder[post_end]
        # rootVal 在中序遍历数组中的索引
        index = self.val_to_index[root_val]
        # 左子树的节点个数
        left_size = index - in_start
        root = TreeNode(root_val) 
        # 递归构造左右子树
        root.left = self.build(inorder, in_start, index - 1,
                               postorder, post_start, post_start + left_size - 1)
        
        root.right = self.build(inorder, index + 1, in_end,
                                postorder, post_start + left_size, post_end - 1)
        return root

889. 根据前序和后序遍历构造二叉树 | 力扣 | LeetCode |

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中任何一个。

示例 1：

输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]

示例 2:

输入: preorder = [1], postorder = [1]
输出: [1]

提示：

1 <= preorder.length <= 30
1 <= preorder[i] <= preorder.length
preorder 中所有值都不同
postorder.length == preorder.length
1 <= postorder[i] <= postorder.length
postorder 中所有值都不同
保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历

基本思路

做这道题之前，建议你先看一下二叉树心法（构造篇），做一下 105. 从前序与中序遍历序列构造二叉树（中等）和 106. 从中序与后序遍历序列构造二叉树（中等）这两道题。

这道题让用后序遍历和前序遍历结果还原二叉树，和前两道题有一个本质的区别：

通过前序中序，或者后序中序遍历结果可以确定一棵原始二叉树，但是通过前序后序遍历结果无法确定原始二叉树。题目也说了，如果有多种结果，你可以返回任意一种。

为什么呢？我们说过，构建二叉树的套路很简单，先找到根节点，然后找到并递归构造左右子树即可。

前两道题，可以通过前序或者后序遍历结果找到根节点，然后根据中序遍历结果确定左右子树。

这道题，你可以确定根节点，但是无法确切的知道左右子树有哪些节点。

举个例子，下面这两棵树结构不同，但是它们的前序遍历和后序遍历结果是相同的：

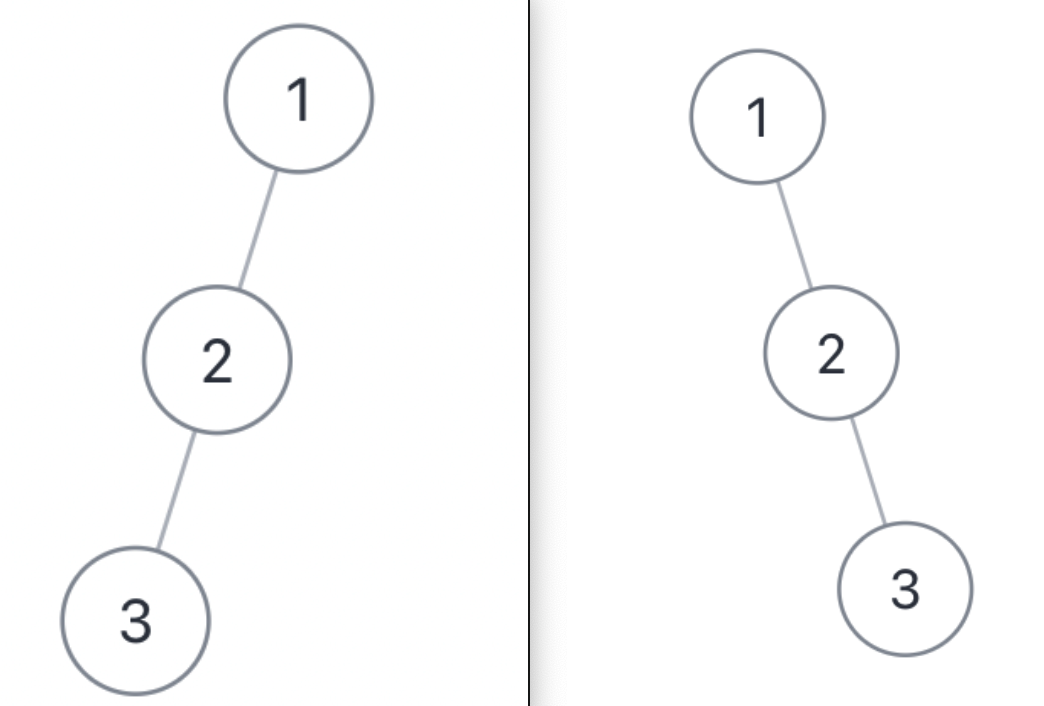
不过话说回来，用后序遍历和前序遍历结果还原二叉树，解法逻辑上和前两道题差别不大，也是通过控制左右子树的索引来构建：

1、首先把前序遍历结果的第一个元素或者后序遍历结果的最后一个元素确定为根节点的值。

2、然后把前序遍历结果的第二个元素作为左子树的根节点的值。

3、在后序遍历结果中寻找左子树根节点的值，从而确定了左子树的索引边界，进而确定右子树的索引边界，递归构造左右子树即可。

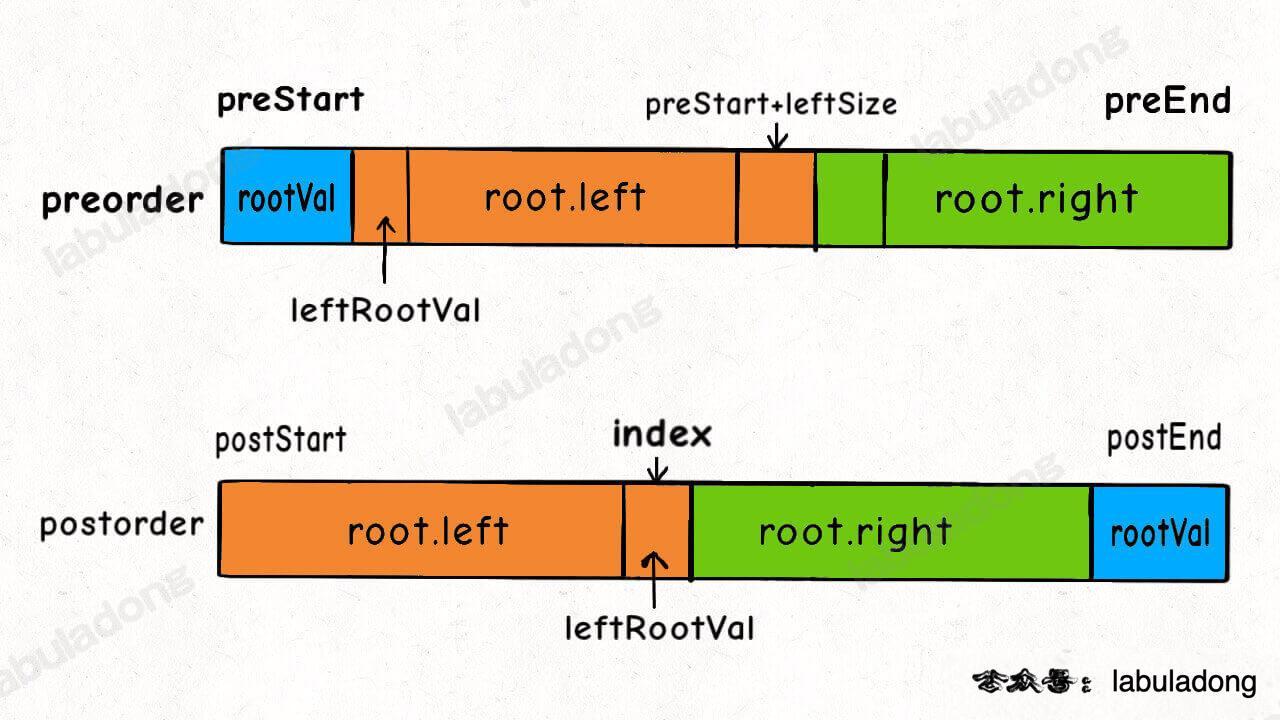
详细题解

class Solution:
    # 存储 postorder 中值到索引的映射
    def __init__(self):
        self.valToIndex = {}

    def constructFromPrePost(self, preorder, postorder):
        for i in range(len(postorder)):
            self.valToIndex[postorder[i]] = i
        return self.build(preorder, 0, len(preorder) - 1,
                          postorder, 0, len(postorder) - 1)

    # 定义：根据 preorder[preStart..preEnd] 和 postorder[postStart..postEnd]
    # 构建二叉树，并返回根节点。
    def build(self, preorder, preStart, preEnd, postorder, postStart, postEnd):
        if preStart > preEnd:
            return None
        if preStart == preEnd:
            return TreeNode(preorder[preStart])

        # root 节点对应的值就是前序遍历数组的第一个元素
        rootVal = preorder[preStart]
        # root.left 的值是前序遍历第二个元素
        # 通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点
        # 确定 preorder 和 postorder 中左右子树的元素区间
        leftRootVal = preorder[preStart + 1]
        # leftRootVal 在后序遍历数组中的索引
        index = self.valToIndex[leftRootVal]
        # 左子树的元素个数
        leftSize = index - postStart + 1

        # 先构造出当前根节点
        root = TreeNode(rootVal)
        # 递归构造左右子树
        # 根据左子树的根节点索引和元素个数推导左右子树的索引边界
        root.left = self.build(preorder, preStart + 1, preStart + leftSize,
                               postorder, postStart, index)
        root.right = self.build(preorder, preStart + leftSize + 1, preEnd,
                                postorder, index + 1, postEnd - 1)

        return root

331. 验证二叉树的前序序列化 | 力扣 | LeetCode |

序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如 #。

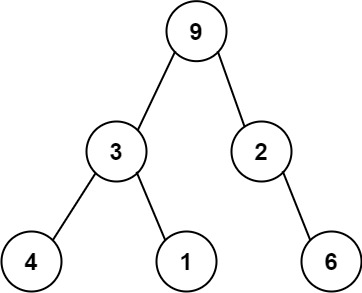
例如，上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#"，其中 # 代表一个空节点。

给定一串以逗号分隔的序列，验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。

保证每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 '#' 。

你可以认为输入格式总是有效的

例如它永远不会包含两个连续的逗号，比如 "1,,3" 。

注意：不允许重建树。

示例 1:

输入: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#"
输出: true

示例 2:

输入: preorder = "1,#"
输出: false

示例 3:

输入: preorder = "9,#,#,1"
输出: false

提示

1 <= preorder.length <= 104
preorder 由以逗号 “，” 分隔的 [0,100] 范围内的整数和 “#” 组成

基本思路

首先，如果看过前文手把手带你刷二叉树（序列化篇）理解了前序遍历序列化和反序列化的原理，肯定可以通过改造反序列化函数 deserialize 来判断序列化的合法性。

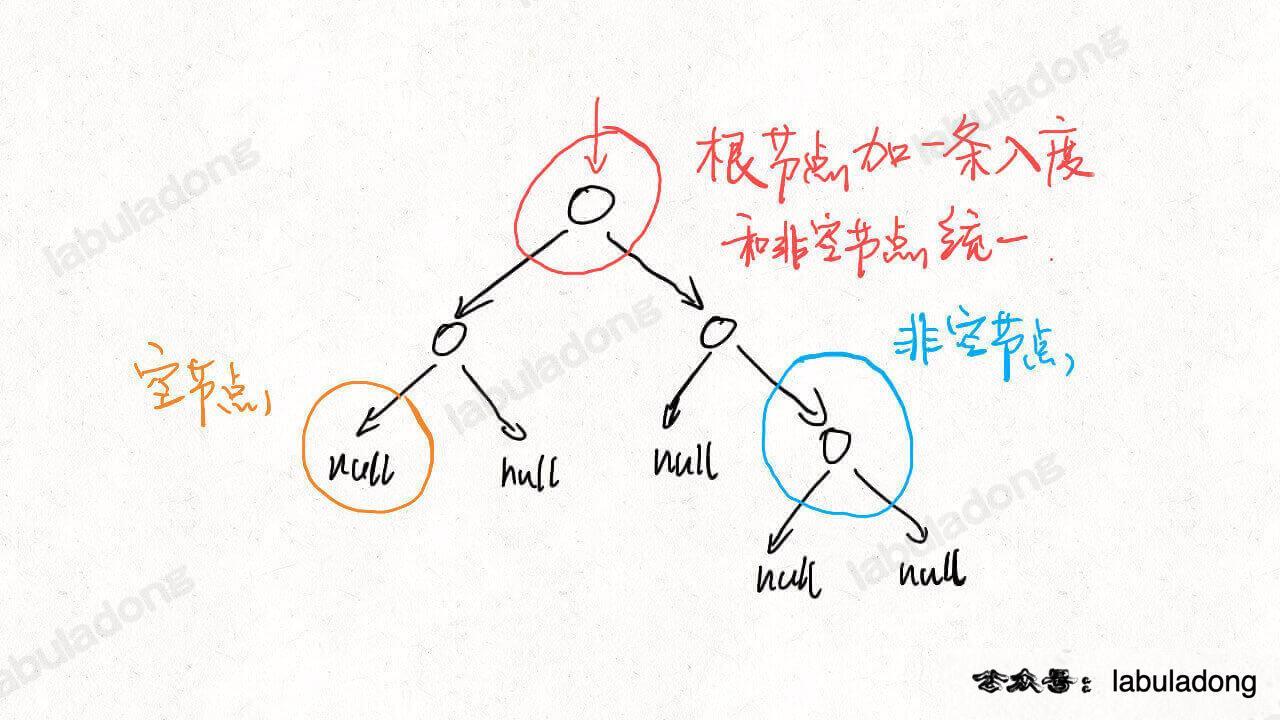
另外还有一种更巧妙的解法，就是利用二叉树节点和边的关系。

每个非空的二叉树节点都会产生两条边，并消耗一条边；而每个空节点只会消耗一条边：

详细题解

class Solution:
    def isValidSerialization(self, preorder: str) -> bool:
        # 一条指向根节点的虚拟边
        edge = 1
        for node in preorder.split(","):
            # 任何时候，边数都不能小于 0
            if node == "#":
                # 空指针消耗一条空闲边
                edge -= 1
                if edge < 0:
                    return False
            else:
                # 非空节点消耗一条空闲边，增加两条空闲边
                edge -= 1
                if edge < 0:
                    return False
                edge += 2
        # 最后不应该存在空闲边
        return edge == 0


class Solution2:
    def isValidSerialization(self, preorder: str) -> bool:
        # 将字符串转化成列表
        nodes = list(preorder.split(","))
        return self.deserialize(nodes) and len(nodes) == 0

    # 改造后的前序遍历反序列化函数
    # 详细解析：https://labuladong.online/algo/data-structure/serialize-and-deserialize-binary-tree/
    def deserialize(self, nodes) -> bool:
        if not nodes:
            return False

        # ***** 前序遍历位置 *****
        # 列表最左侧就是根节点
        first = nodes.pop(0)
        if first == "#":
            return True
        # *********************

        return self.deserialize(nodes) and self.deserialize(nodes)

654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

示例 1：

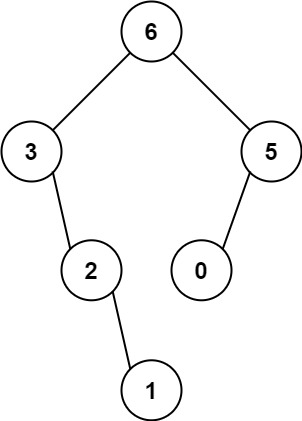
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：
- [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
        - 空数组，无子节点。
        - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
            - 空数组，无子节点。
            - 只有一个元素，所以子节点是一个值为 1 的节点。
    - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
        - 只有一个元素，所以子节点是一个值为 0 的节点。
        - 空数组，无子节点。

示例 2：

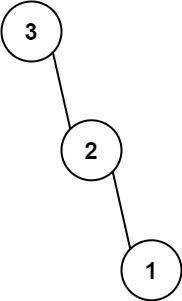
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

提示：

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同

基本思路

前文手把手刷二叉树总结篇说过二叉树的递归分为「遍历」和「分解问题」两种思维模式，这道题需要用到「分解问题」的思维。

做这道题之前，你一定要去做一下 654. 最大二叉树这道题，知道了构建最大二叉树的逻辑就很容易解决这道题了。

新增的 val 是添加在原始数组的最后的，根据构建最大二叉树的逻辑，正常来说最后的这个值一定是在右子树的，可以对右子树递归调用 insertIntoMaxTree 插入进去。

但是一种特殊情况是 val 比原始数组中的所有元素都大，那么根据构建最大二叉树的逻辑，原来的这棵树应该成为 val 节点的左子树。

详细题解

class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
        def construct(left: int, right: int) -> Optional[TreeNode]:
            if left > right:
                return None
            
            best = left
            for i in range(left + 1, right + 1):
                if nums[i] > nums[best]:
                    best = i
        
            node = TreeNode(nums[best])
            node.left = construct(left, best - 1)
            node.right = construct(best + 1, right)
            return node
        
        return construct(0, len(nums) - 1)

998. 最大二叉树 II | 力扣 | LeetCode |

最大树 定义：一棵树，并满足：其中每个节点的值都大于其子树中的任何其他值。

给你最大树的根节点 root 和一个整数 val 。

就像之前的问题那样，给定的树是利用 Construct(a) 例程从列表 a（root = Construct(a)）递归地构建的：

如果 a 为空，返回 null 。
否则，令 a[i] 作为 a 的最大元素。创建一个值为 a[i] 的根节点 root 。
root 的左子树将被构建为 Construct([a[0], a[1], ..., a[i - 1]]) 。
root 的右子树将被构建为 Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]]) 。
返回 root 。

请注意，题目没有直接给出 a ，只是给出一个根节点 root = Construct(a) 。

假设 b 是 a 的副本，并在末尾附加值 val。题目数据保证 b 中的值互不相同。

返回 Construct(b) 。

示例 1：

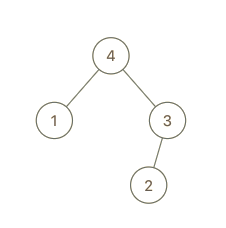
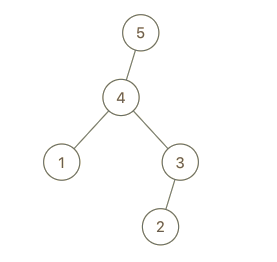
输入：root = [4,1,3,null,null,2], val = 5
输出：[5,4,null,1,3,null,null,2]
解释：a = [1,4,2,3], b = [1,4,2,3,5]

示例 2：

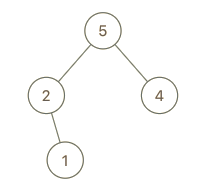
输入：root = [5,2,4,null,1], val = 3
输出：[5,2,4,null,1,null,3]
解释：a = [2,1,5,4], b = [2,1,5,4,3]

示例 3：

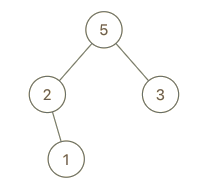
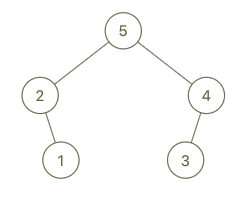
输入：root = [5,2,3,null,1], val = 4
输出：[5,2,4,null,1,3]
解释：a = [2,1,5,3], b = [2,1,5,3,4]

提示：

树中节点数目在范围 [1, 100] 内
1 <= Node.val <= 100
树中的所有值 互不相同
1 <= val <= 100

基本思路

前文手把手刷二叉树总结篇说过二叉树的递归分为「遍历」和「分解问题」两种思维模式，这道题需要用到「分解问题」的思维。

做这道题之前，你一定要去做一下 654. 最大二叉树这道题，知道了构建最大二叉树的逻辑就很容易解决这道题了。

但是一种特殊情况是 val 比原始数组中的所有元素都大，那么根据构建最大二叉树的逻辑，原来的这棵树应该成为 val 节点的左子树。

详细题解

class Solution:
    def insertIntoMaxTree(self, root: TreeNode, val: int) -> TreeNode:
        if root is None:
            return TreeNode(val)
        if root.val < val:
            # 如果 val 是整棵树最大的，那么原来的这棵树应该是 val 节点的左子树，
            # 因为 val 节点是接在原始数组 a 的最后一个元素
            temp = root
            root = TreeNode(val)
            root.left = temp
        else:
            # 如果 val 不是最大的，那么就应该在右子树上，
            # 因为 val 节点是接在原始数组 a 的最后一个元素
            root.right = self.insertIntoMaxTree(root.right, val)
        return root

1110. 删点成林 | 力扣 | LeetCode |

给出二叉树的根节点 root，树上每个节点都有一个不同的值。

如果节点值在 to_delete 中出现，我们就把该节点从树上删去，最后得到一个森林（一些不相交的树构成的集合）。

返回森林中的每棵树。你可以按任意顺序组织答案。

示例 1：

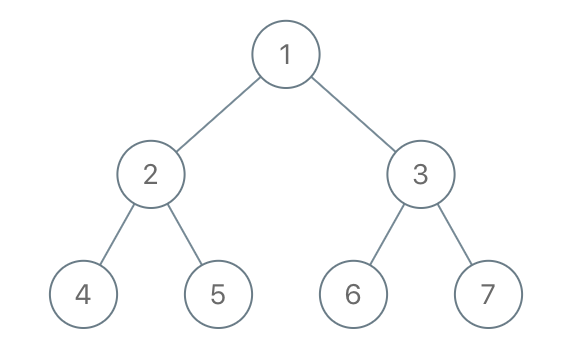
输入：root = [1,2,3,4,5,6,7], to_delete = [3,5]
输出：[[1,2,null,4],[6],[7]]

示例 2：

输入：root = [1,2,4,null,3], to_delete = [3]
输出：[[1,2,4]]

提示：

树中的节点数最大为 1000。
每个节点都有一个介于 1 到 1000 之间的值，且各不相同。
to_delete.length <= 1000
to_delete 包含一些从 1 到 1000、各不相同的值。

基本思路

前文手把手刷二叉树总结篇说过二叉树的递归分为「遍历」和「分解问题」两种思维模式，这道题需要用到「分解问题」的思维。

首先，如果在递归过程中修改二叉树结构，必须要让父节点接收递归函数的返回值，因为子树不管删成啥样，都要接到父节点上。

而且，手把手刷二叉树总结篇说了可以通过函数参数传递父节点传递的数据，所以可以在前序位置判断是否得到了一个新的根节点。

详细题解

class Solution:
    def __init__(self):
        self.delSet = set()
        # 记录森林的根节点
        self.res = []

    def delNodes(self, root, to_delete):
        if root is None:
            return []
        for d in to_delete:
            self.delSet.add(d)
        self.doDelete(root, False)
        return self.res

    # 定义：输入一棵二叉树，删除 delSet 中的节点，返回删除完成后的根节点
    def doDelete(self, root, hasParent):
        if root is None:
            return None
        # 判断是否需要被删除
        deleted = root.val in self.delSet
        if not deleted and not hasParent:
            # 没有父节点且不需要被删除，就是一个新的根节点
            self.res.append(root)
        # 去左右子树进行删除
        root.left = self.doDelete(root.left, not deleted)
        root.right = self.doDelete(root.right, not deleted)
        # 如果需要被删除，返回 null 给父节点
        return None if deleted else root

1485. 克隆含随机指针的二叉树 | 力扣 | LeetCode |

给你一个二叉树，树中每个节点都含有一个附加的随机指针，该指针可以指向树中的任何节点或者指向空（null）。

请返回该树的 深拷贝 。

该树的输入/输出形式与普通二叉树相同，每个节点都用 [val, random_index] 表示：

val：表示 Node.val 的整数
random_index：随机指针指向的节点（在输入的树数组中）的下标；如果未指向任何节点，则为 null 。

该树以 Node 类的形式给出，而你需要以 NodeCopy 类的形式返回克隆得到的树。NodeCopy 类和Node 类定义一致。

示例 1：

输入：root = [[1,null],null,[4,3],[7,0]]
输出：[[1,null],null,[4,3],[7,0]]
解释：初始二叉树为 [1,null,4,7] 。
节点 1 的随机指针指向 null，所以表示为 [1, null] 。
节点 4 的随机指针指向 7，所以表示为 [4, 3] 其中 3 是树数组中节点 7 对应的下标。
节点 7 的随机指针指向 1，所以表示为 [7, 0] 其中 0 是树数组中节点 1 对应的下标。

示例 2：

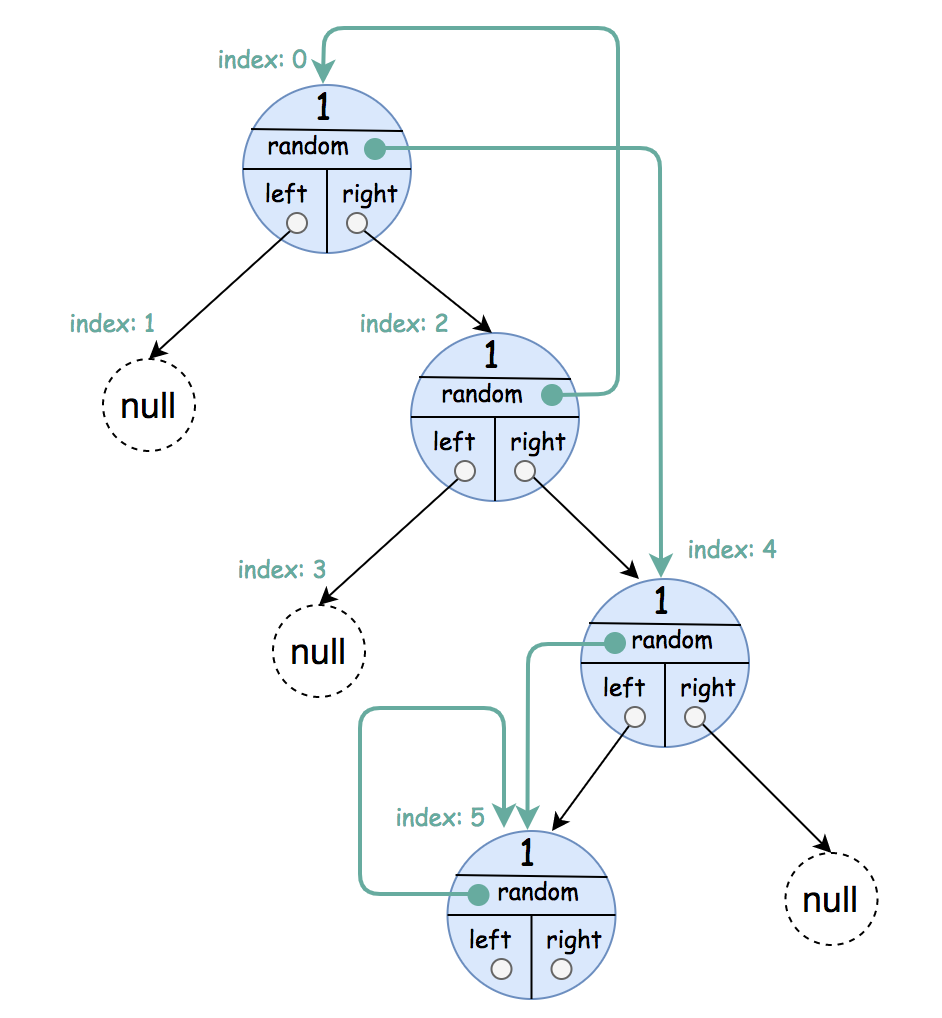
输入：root = [[1,4],null,[1,0],null,[1,5],[1,5]]
输出：[[1,4],null,[1,0],null,[1,5],[1,5]]
解释：节点的随机指针可以指向它自身。

示例 3：

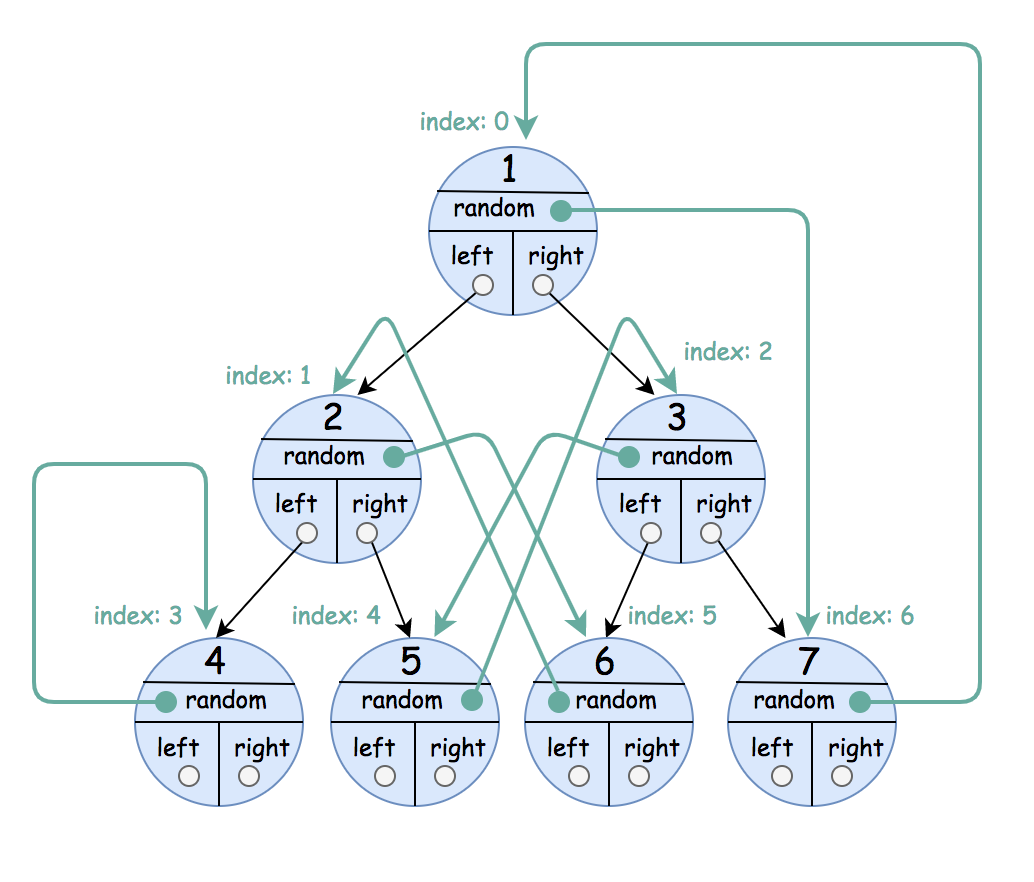
输入：root = [[1,6],[2,5],[3,4],[4,3],[5,2],[6,1],[7,0]]
输出：[[1,6],[2,5],[3,4],[4,3],[5,2],[6,1],[7,0]]

提示：

tree 中节点数目范围是 [0, 1000]
每个节点的值的范围是 [1, 10^6]

基本思路

这道题和一般的二叉树构造问题思路是一样的，函数的定义就是复制二叉树并返回根节点，那么把根节点构造出来之后，递归调用子节点就行了，基本算法框架肯定是这样：

// 定义：输入一棵二叉树的根节点 root，复制这棵树并返回复制后的根节点
public NodeCopy copyRandomBinaryTree(Node root) {
    if (root == null) {
        return null;
    }
    NodeCopy rootCopy = new NodeCopy(root.val);
    // 根据函数定义递归构造三个子节点
    rootCopy.left = copyRandomBinaryTree(root.left);
    rootCopy.right = copyRandomBinaryTree(root.right);
    rootCopy.random = copyRandomBinaryTree(root.random);

    return rootCopy;
}

但这道题的特殊之处在于 random 节点，可能指向任何节点，如果这个节点还没被构建出来，你应该把它 new 出来，但如果这个节点已经被构建出来了，你直接把 random 指针指向这个节点就行了。

想做到这一点也很简单，用一个 HashMap 存储原始节点到复制节点的映射就行了，这样就能知道哪些节点已经被构建出来了。

详细题解

class Solution:
    # 原始节点到复制节点的映射
    def __init__(self):
        self.node_to_copy = {}

    # 定义：输入一棵二叉树的根节点 root，复制这棵树并返回复制后的根节点
    def copyRandomBinaryTree(self, root):
        # 一个节点需要做的事情
        if root is None:
            return None
        if root in self.node_to_copy:
            return self.node_to_copy[root]
        # 在前序位置把自己存入 map 映射，之后如果有 random 指针
        # 指向自己的话可以直接从 map 里面拿出来
        root_copy = NodeCopy(root.val)
        self.node_to_copy[root] = root_copy

        # 根据函数定义递归构造三个子节点
        root_copy.left = self.copyRandomBinaryTree(root.left)
        root_copy.right = self.copyRandomBinaryTree(root.right)
        root_copy.random = self.copyRandomBinaryTree(root.random)

        return root_copy

1660. 纠正二叉树 | 力扣 | LeetCode |

你有一棵二叉树，这棵二叉树有个小问题，其中有且只有一个无效节点，它的右子节点错误地指向了与其在同一层且在其右侧的一个其他节点。

给定一棵这样的问题二叉树的根节点 root ，将该无效节点及其所有子节点移除（除被错误指向的节点外），然后返回新二叉树的根结点。

自定义测试用例：

测试用例的输入由三行组成：

TreeNode root
int fromNode （在 correctBinaryTree 中不可见）
int toNode （在 correctBinaryTree 中不可见）

当以 root 为根的二叉树被解析后，值为 fromNode 的节点 TreeNode 将其右子节点指向值为 toNode 的节点 TreeNode 。然后， root 传入 correctBinaryTree 的参数中。

示例 1:

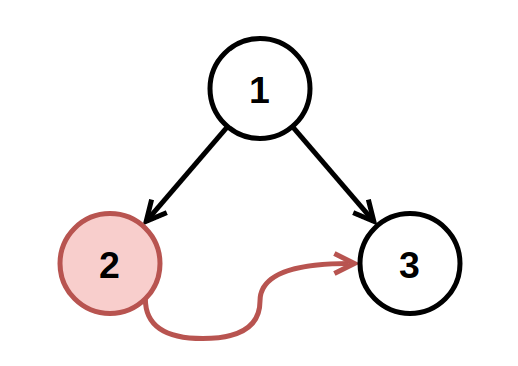
输入: root = [1,2,3], fromNode = 2, toNode = 3
输出: [1,null,3]
解释: 值为 2 的节点是无效的，所以移除之。

示例 2:

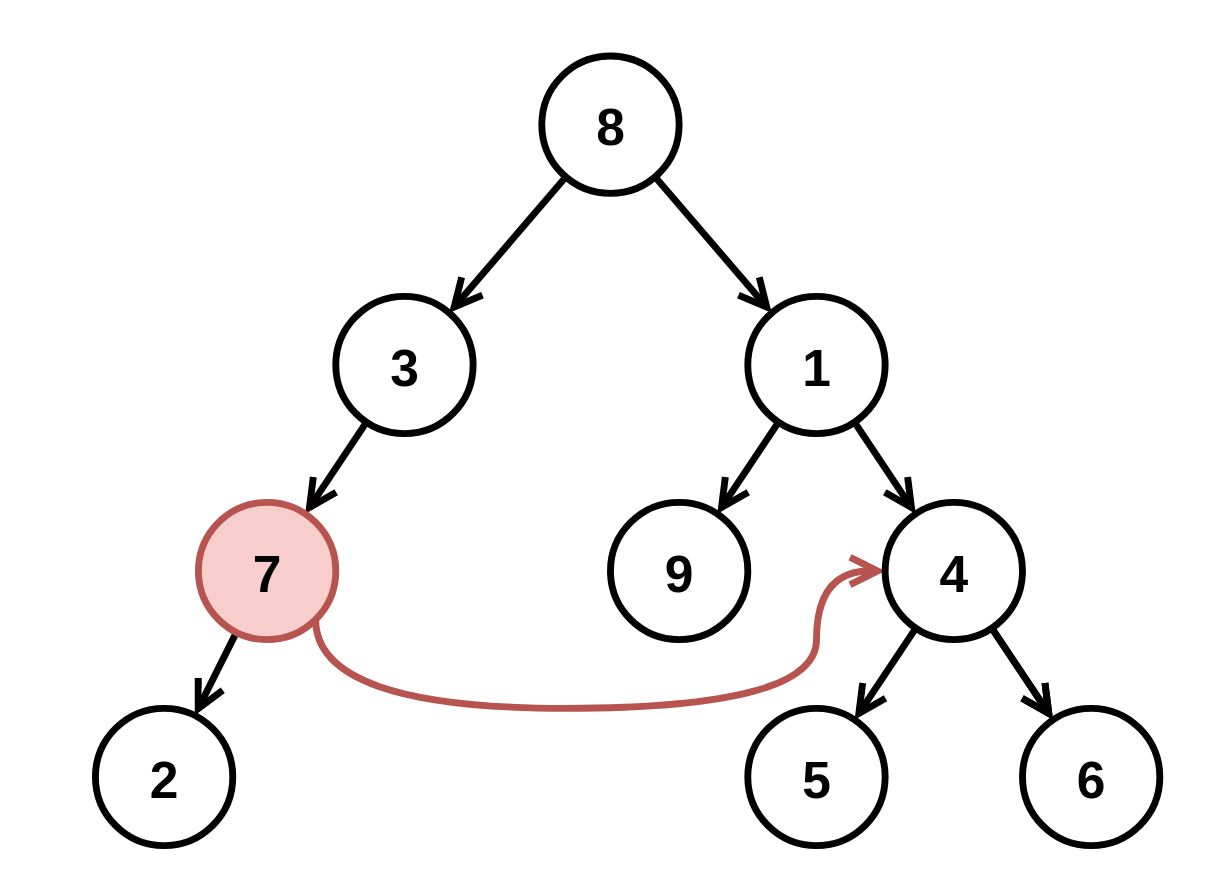
输入: root = [8,3,1,7,null,9,4,2,null,null,null,5,6], fromNode = 7, toNode = 4
输出: [8,3,1,null,null,9,4,null,null,5,6]
解释: 值为 7 的节点是无效的，所以移除这个节点及其子节点 2。

提示:

树中节点个数的范围是 [3, 104] 。
-109 <= Node.val <= 109
所有的 Node.val 都是互不相同的。
fromNode != toNode
fromNode 和 toNode 将出现在树中的同一层。
toNode 在 fromNode 的右侧。
fromNode.right 在测试用例的树中建立后为 null 。

基本思路

这道题要求你熟悉如何构造二叉树，而且还要理解二叉树的遍历顺序。

如何知道一个节点 x 是「错误」节点？

需要要知道它的右子节点错误地指向同层右侧的一另一个节点。

那么如何让节点 x 知道自己错指了呢？

如果用层序遍历的方式应该比较容易想到解法，我们可以从右向左遍历每一行的节点并记录下来访问过的节点，如果你发现某个节点 x 的右子节点已经被访问过，那么这个节点 x 就是错误节点。

如果用递归遍历的方式，如何做到「从右向左」遍历每一行的节点呢？只要稍微改一下二叉树的遍历框架，先遍历右子树后遍历左子树，这样就是先遍历右侧节点后遍历左侧节点，也就相当于从右向左遍历了。

同理，遍历的时候我们同时记录已遍历的节点。这样 x 如果发现自己的右子节点已经被访问了，就说明 x 节点是「错误」的。具体思路见代码注释。

详细题解

class Solution:
    # 记录已访问过的节点
    visited = set()

    def correctBinaryTree(self, root: TreeNode) -> TreeNode:
        if root is None:
            return None
        if root.right is not None and root.right in self.visited:
            # 找到「无效节点」，删除整棵子树
            return None
        self.visited.add(root)
        # 要先遍历右子树，后遍历左子树
        root.right = self.correctBinaryTree(root.right)
        root.left = self.correctBinaryTree(root.left)
        return root

查看全文

http://www.kler.cn/a/388210.html