A算法详解(go实现)
A*算法详解(go实现)
推荐一位大佬的文章,建议可以去看看https://hogwartsrico.github.io/2016/03/11/AStarPathFinding/index.html
下面贴出来文章中用于举例的网站:
https://anvaka.github.io/ngraph.path.demo/#?graph=amsterdam-roads&fromId=-1&toId=-1
https://www.hightopo.com/demo/astar/astar.html
等了解了具体的原理,可以试着来写一个地图上最短路径的实现或者是ai寻路的小游戏啥的,下面还是先看看什么是A*吧!
一、什么是A*?
A*(A-Star)寻路算法是一种用于在图或网格中寻找从起点到终点的最短路径的算法,通常用于机器人导航、游戏开发中的角色路径规划等,比如王者里面的人机怎么知道要从泉水回到线上吃经济呢,原理就是A*。
我们知道Dijkstra算法给出的结果是最优,但是计算量大导致速度大打折扣,贪心算法呢?虽然速度快,但是结果并不完全是最优的,所以二者优点相结合,引入启发式策略诞生了A*算法,是能够兼顾速度和最优解的存在。它的独特之处是检查最短路径中每个可能的节点时引入了全局信息,对当前节点距终点的距离做出估计,并作为评价该节点处于最短路线上的可能性的量度。
(https://qiao.github.io/PathFinding.js/visual/可以使用这个网址来比较一下这些算法的差别)
基本原理
A*算法使用一种启发式估价函数来引导搜索过程,选择更可能接近目标的路径。它维护一个开放列表(open list)和一个关闭列表(close list),并计算每个节点的总代价值 f 来决定路径。算法在每个步骤中从开放列表中选择代价最低的节点进行扩展,直到找到终点或者确认没有路径。
简单来说就是从A到B,不断地计算总代价值 f,来判断下次探索的方向,每个节点的值计算方法为:**F(N)=G(N)+H(N)**(代价函数)
其中G(N)是从起点到当前节点N的移动消耗;H(N)代表当前节点到目标节点的预期距离,可以用使用曼哈顿距离、欧氏距离等。
值得注意的是:当节点间移动消耗G(N)非常小时,G(N)对F(N)的影响也会微乎其微,A算法就退化为最好优先贪婪算法;当节点间移动消耗G(N)非常大以至于H(N)对F(N)的影响微乎其微时,A算法就退化为Dijkstra算法。
二、关键词介绍
1、节点(Node):
路径中的每个位置被看作是一个节点。节点包含信息:位置、代价值、父节点(用来回溯路径)。
2、代价函数 f(n):
A* 算法基于每个节点的代价 f(n) 来选择最优路径节点。
公式:
f(n) = g(n) + h(n)
g(n):从起点到当前节点的实际代价(通常是路径长度)。h(n):从当前节点到终点的估计代价,即启发式值(Heuristic)。f(n):总代价值,用于在候选路径中选择当前最佳路径。
3、启发式函数 h(n):
h(n)是对当前位置到目标位置的估计距离,影响算法的搜索方向。启发式函数的设计决定了算法的性能和结果。
常用启发式函数:
- 曼哈顿距离:用于网格或直角运动。
- 欧几里得距离:适合自由运动的空间。
- 对角距离:适合八方向(包括对角线)移动的网格。
4、开放列表(Open List)和关闭列表(Close List):
开放列表:存储候选节点,每次选择其中 f 值最低的节点作为扩展节点。
关闭列表:存储已访问的节点,以防重复计算和路径循环。
三、算法步骤
使用上述文章中的图片来做解释,作者使用的启发式函数是对角距离,也就是八方向(包括对角线)移动的网格
-
初始化:
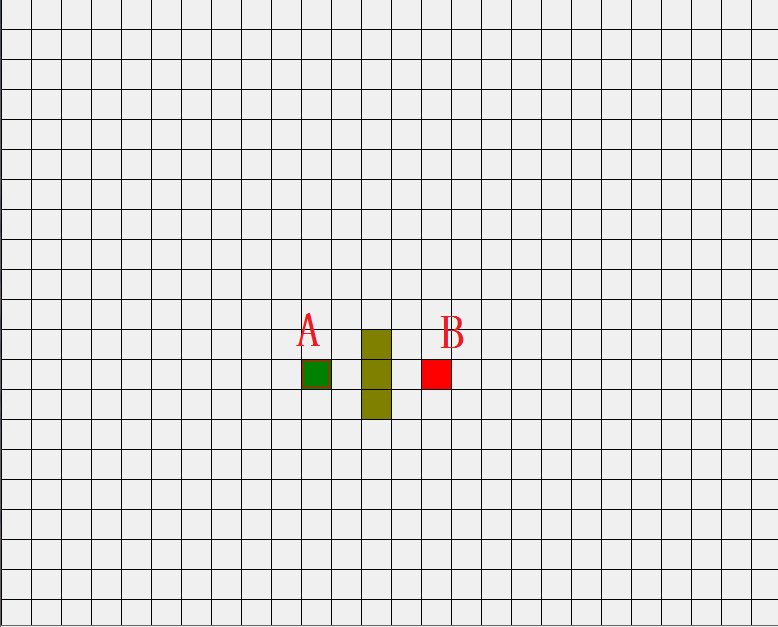
如图所示简易网格地图,其中绿色方块的是起点 (用 A 表示), 中间绿色的是障碍物(不可走), 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块.。
-
起点A加入openlist*,相邻方格加入OpenList,并设置parent**
将起始节点放入开放列表,计算其
f值(起点的g为0,h为启发式估计到终点的距离)找到与起点 A 相邻的方格 ,把其中可走的方格也加入到 OpenList 中(忽略阻碍方格)**。把起点 A 设置为这些方格的父亲 (parent node)
(左下角是g,左上角是f,对角距离当作1)
-
A从OpenList移除,加入CloseList
把 A 从 OpenList 中移除,加入到 CloseList( 封闭列表,其中的方格在之后的搜寻中都不再考虑 ) 中, CloseList 中的每个方格都是现在不需要再关注的。下一步,我们需要从 OpenList 中选一个与起点 A 相邻的方格,按下面描述的一样或多或少的重复前面的步骤。但是到底选择哪个方格好呢?具有最小 F 值的那个。
-
路径排序
计算出组成路径的方格的关键是下面这个等式:
F = G + H这里 ,
G = 从起点 A 移动到指定方格的移动代价,沿着到达该方格而生成的路径。
H = 从指定的方格移动到终点 B 的估算成本。
我们的路径是这么产生的:反复遍历 OpenList ,选择 F 值最小的方格。
如上所述, G 是从起点A移动到指定方格的移动代价。在本例中,横向,纵向,斜角的移动代价为 1 (也可以将斜角代价设为1.4–2的平方根) 这里就用1了
既然我们是沿着到达指定方格的路径来计算 G 值,那么计算出该方格的 G 值的方法就是找出其父亲的 G 值,然后按父亲是直线方向还是斜线方向加上1 。随着我们离开起点而得到更多的方格,这个方法会变得更加明朗。
我们对上图 补上FGH值 拿右下角这个方格距离,它离起点差1个斜对角,G等于1 离终点差4个方格,所以F等于
1+4 = 5,其他方格同理, F 值,直接把 G 值和 H 值相加就可以了。
-
继续搜索,选出最小F值的方格,移出OpenList,加入ClostList

-
检查所有与它相邻的方格,忽略在CloseList 中或是阻碍的方格
衍生出2种情况:
如果方格不在OpenList 中,则把它们加入到 OpenList 中,把我们选定的方格设置为这些新加入的方格的父亲。
如果这个点的相邻方格已经在OpenList中,则重计算F值(由这个点为起点到达该相邻点的F值),并将它和之前的F值作比较,又衍生出2种情况:
如果新的F值小于旧的F值,说明由这个点去往该相邻点的路近了,选定这个点为下一个处理点,并将该相邻点的父亲设为它,更新该相邻点的FGH值.
如果不是,啥也不做(上一步可知其实该点已经被剔除OpenList加入ClostList中了)。

它右边的方格是墙壁,我们忽略。它左边的方格是起点,在 CloseList 中,我们也忽略。其他 4 个相邻的方格(红色五角星)均在 OpenList 中,我们需要检查经由这个方格到达那里的路径是否更好,使用 G 值来判定。
让我们看看上面的方格。它现在的 G 值为 1 。如果我们经由当前方格到达那里, G 值将会为 2(其中 1 为到达当前方格的 G 值,此外还要加上从当前方格纵向移动到上面方格的 G 值 1) 。显然 2 比 1 大,因此这不是最优的路径。如果你看图你就会明白。直接从起点沿对角线移动到那个方格比先横向移动再纵向移动要好。
7.我们选择起点右上方的方格
如下图所示:
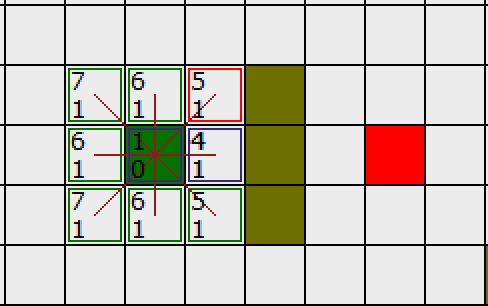
右上的方格已经被标为红色框,我们同时也可以看到起点和右侧点外框都已经是蓝色了说明他们已经被加入ClostList中不再被考虑了
8.重复上述操作,直至出现了终点


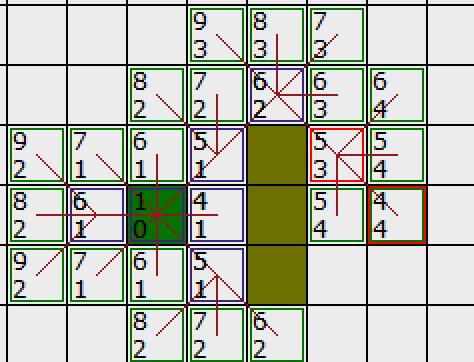

看一下动图:

四、go语言代码实现
package main
import (
"fmt"
"math"
"sort"
"strings"
)
var openlist []*open
var closelist []*pos
func isIncloselist(x, y int) bool {
for _, pos := range closelist {
if pos.y == y && pos.x == x {
return true
}
}
return false
}
func isInopenlist(x, y int) (*open, bool) {
for _, o := range openlist {
if o.pos.y == y && o.pos.x == x {
return o, true
}
}
return nil, false
}
type open struct {
parent *open
pos *pos
f int
g int
h int
}
type pos struct {
x int
y int
view string
}
type maps struct {
with int
height int
zones []*pos
}
// findAstarPaths A星寻路算法获取地图中起始点至终点的路径
func (m *maps) findAstarPaths(startX, startY, endX, endY int) []*pos {
defer func() {
openlist = nil
closelist = nil
}()
startPos := m.getpos(startX, startY)
endPos := m.getpos(endX, endY)
if startPos == nil || endPos == nil || endPos.view == "X" || startPos.view == "X" {
return nil
}
if startPos.x == endPos.x && startPos.y == endPos.y {
return []*pos{startPos}
}
openlist = append(openlist, &open{pos: startPos})
var lastopen *open
for len(openlist) > 0 {
// 找到最小的F值的点
sort.Slice(openlist, func(i, j int) bool { return openlist[i].f < openlist[j].f })
minopen := openlist[0]
openlist = openlist[1:]
closelist = append(closelist, minopen.pos)
// 1、找到F点周围的点(八个方向)如果是墙或在closelist中或超出地图范围则跳过
// 2、如果在openlist中则判断G值是否比之前大,如果是则不处理,否则更新这个点的父亲节点为当前节点并重新计算F值
// 3、如果终点已经在openlist中说明已经找到最优路径,退出查找
/** 上 **/
lastopen = m.findLastOpen(minopen, minopen.pos.x, minopen.pos.y-1, endX, endY, 10)
if lastopen != nil {
break
}
/** 下 **/
lastopen = m.findLastOpen(minopen, minopen.pos.x, minopen.pos.y+1, endX, endY, 10)
if lastopen != nil {
break
}
/** 左 **/
lastopen = m.findLastOpen(minopen, minopen.pos.x-1, minopen.pos.y, endX, endY, 10)
if lastopen != nil {
break
}
/** 右 **/
lastopen = m.findLastOpen(minopen, minopen.pos.x+1, minopen.pos.y, endX, endY, 10)
if lastopen != nil {
break
}
/** 左上 **/
lastopen = m.findLastOpen(minopen, minopen.pos.x-1, minopen.pos.y-1, endX, endY, 14)
if lastopen != nil {
break
}
/** 左下 **/
lastopen = m.findLastOpen(minopen, minopen.pos.x-1, minopen.pos.y+1, endX, endY, 14)
if lastopen != nil {
break
}
/** 右上 **/
lastopen = m.findLastOpen(minopen, minopen.pos.x+1, minopen.pos.y-1, endX, endY, 14)
if lastopen != nil {
break
}
/** 右下 **/
lastopen = m.findLastOpen(minopen, minopen.pos.x+1, minopen.pos.y+1, endX, endY, 14)
if lastopen != nil {
break
}
}
if lastopen == nil {
return nil
}
var paths []*pos
for lastopen != nil {
if len(paths) == 0 {
paths = append(paths, lastopen.pos)
} else {
tmp := make([]*pos, len(paths)+1)
tmp[0] = lastopen.pos
copy(tmp[1:], paths)
paths = tmp
}
lastopen = lastopen.parent
}
return paths
}
func (m *maps) print() {
for y := 0; y < m.height; y++ {
for x := 0; x < m.with; x++ {
fmt.Print(" " + m.getpos(x, y).view + " ")
}
fmt.Println()
}
}
func (m *maps) getpos(x, y int) *pos {
if x < 0 || y < 0 || x >= m.with || y >= m.height {
return nil
}
for _, pos := range m.zones {
if pos.y == y && pos.x == x {
return pos
}
}
return nil
}
func (m *maps) updateView(x, y int, view string) {
p := m.getpos(x, y)
if p != nil {
p.view = view
}
}
func (m *maps) findLastOpen(minopen *open, findX, findY, endX, endY int, gval int) *open {
if findX == endX && findY == endY {
return &open{pos: m.getpos(endX, endY), parent: minopen}
}
findPos := m.getpos(findX, findY)
if findPos == nil || findPos.view != "O" || isIncloselist(findX, findY) {
return nil
}
currentopen := &open{
pos: findPos,
g: minopen.g + gval,
}
currentopen.h = int(math.Abs(float64(endY-currentopen.pos.y))*10 + math.Abs(float64(endX-currentopen.pos.x)*10))
currentopen.f = currentopen.h + currentopen.g
currentopen.parent = minopen
// 判断是否在opendlist中
open, b := isInopenlist(findX, findY)
if b {
if open.g > currentopen.g {
open.parent = minopen
open.g = currentopen.g
open.f = open.g + open.h
}
} else {
openlist = append(openlist, currentopen)
}
return nil
}
func newMaps(arr []string) *maps {
m := &maps{
with: len(strings.Split(arr[0], " ")),
height: len(arr),
}
for y := 0; y < m.height; y++ {
viewArr := strings.Split(arr[y], " ")
for x := 0; x < m.with; x++ {
m.zones = append(m.zones, &pos{x, y, viewArr[x]})
}
}
return m
}
func main() {
arr := []string{
"O X O O X",
"O O O X O",
"O X X O O",
"O X O X O",
"O X O X O",
}
m := newMaps(arr)
m.print()
fmt.Println("----------- 寻路结果 ----------")
paths := m.findAstarPaths(0, 0, 4, 4)
if len(paths) == 0 {
fmt.Println("没有合适的路径")
return
}
for i, pos := range paths {
if i == 0 {
m.updateView(pos.x, pos.y, "S")
} else if i == len(paths)-1 {
m.updateView(pos.x, pos.y, "E")
} else {
m.updateView(pos.x, pos.y, "*")
}
}
m.print()
}
参考文章:A星寻路算法解析 | Rico’s Blog
路径规划(五)-A-Star算法 | 学步
使用GO语言实现A星寻路算法 - OSCHINA - 中文开源技术交流社区
后面将会开源坦克动荡go语言版的,包括超强人机(寻路就是使用a*实现的)和联机功能,也鼓励大家使用该算法实现一些有趣的项目
