革新预测领域:频域融合时间序列预测,深度学习新篇章,科研涨点利器
2024发论文&模型涨点之——频域+时间序列
频域+时间序列不仅能提供更丰富的信息,还能提高模型性能和预测准确性。对于论文er来说,是个可发挥空间大、可挖掘创新点多的研究方向。当前,学术界的目光正聚焦于时频融合这一前沿趋势,尤其是在今年的顶级学术会议中,频域分析已成为热议焦点。这一趋势预示着,掌握时频结合技术的学者将在科研道路上占据先机,发表高质量论文、提升学术影响力的机会正悄然而至。目前,时域分析和频域分析已经成为了时间序列领域的重要工具,频域相关也逐渐成了顶会常客。
为帮助同学们获取论文,小编整理了一些频域+时间序列论文合集,论文原文+开源代码需要的同学关注“AI科研灵感”公号,那边回复“频域+时间序列”获取。
论文1:
A framework for assessing frequency domain causality in physiological time series with instantaneous effects
用于评估生理时间序列中即时效应的频域因果关系的框架
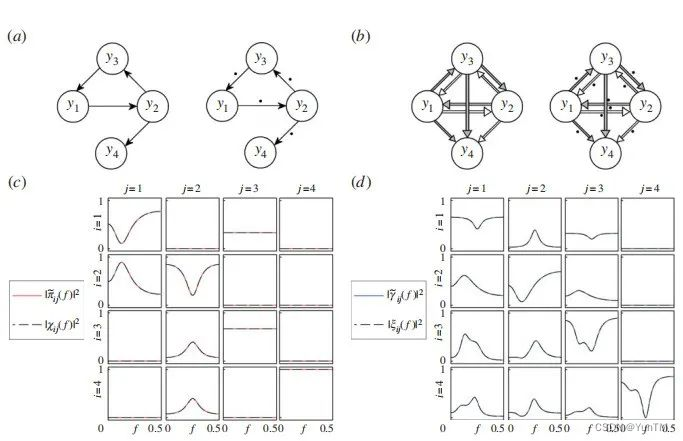
方法
因果性评估:提出了一种新的方法来量化多时间序列中的因果关系,特别是那些具有显著零滞后交互作用的序列。
扩展MVAR模型:引入了扩展的多变量自回归(eMVAR)框架,允许考虑时间滞后效应和即时效应。
频域因果性度量:利用eMVAR模型的谱表示,推导出新的频域因果性度量,这些度量能够概括即时效应的已知方向相干(DC)和部分DC(PDC)度量。
模型识别和验证:提出了两种模型识别方法,并讨论了与模型假设相关的潜在问题,包括白噪声检验和独立性检验。
创新点
即时效应的考虑:首次在频域因果性分析中同时考虑了即时和滞后效应,扩展了传统的Granger因果性定义。
新度量方法的提出:提出了新的频域因果性度量方法,这些方法能够描述多序列间复杂的方向性交互作用,尤其是在即时因果性不可忽视时。
模型识别的创新方法:提出了基于先验结构的eMVARis方法和基于非高斯性的eMVARng方法,以解决即时效应模型的识别问题。
论文2:
Frequency-domain MLPs are More Effective Learners in Time Series Forecasting频域MLP在时间序列预测中是更有效的学习器
方法
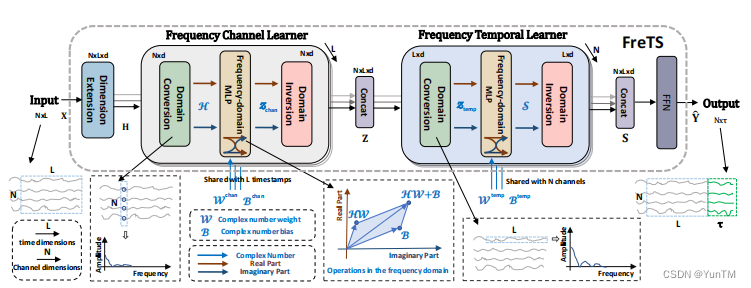
频域MLPs:探索了在频域中应用多层感知器(MLPs)进行时间序列预测的新方向。
FreTS架构:提出了一个简单而有效的基于频域MLPs的时间序列预测架构FreTS,包括域转换和频域学习两个阶段。
域转换:将时间域信号转换为频域复数。
频域学习:对频域分量的实部和虚部进行MLP学习,以恢复最终预测。
创新点
全局视角和能量压缩:发现频域MLPs能够捕获更明显的全局周期性模式,并且能够更清晰地识别对角线依赖性和关键模式。
FreTS架构的提出:提出了一个新颖的架构,该架构在频域中学习时间序列预测映射,有效地结合了通道和时间依赖性。
实验验证:在13个真实世界的基准测试中(包括短期和长期预测),展示了FreTS相比现有最先进方法的优越性。
论文3:
Combining Time Series and Frequency Domain Analysis for Automatic Seizure Detection
结合时间序列和频域分析进行自动癫痫发作检测
方法
EpiScan算法:利用连续小波变换方法识别具有节律性或周期性形态的癫痫活动。
EWS分析:提出了一种新的时域方法,用于检测具有不规则和扭曲节律活动的癫痫发作模式。
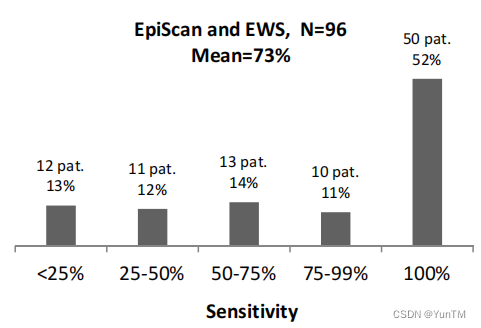
性能分析:通过敏感性和误报率来评估检测性能,使用AIT EEG数据库进行验证。
创新点
EWS算法的提出:首次提出了一种时域算法EWS,用于检测具有不规则结构、突发相位变化或扭曲的癫痫发作模式。
EWS与EpiScan的结合:通过结合EWS算法和EpiScan算法,提高了检测敏感性,同时降低了误报率。
检测性能的提升:在AIT EEG数据库上测试表明,结合使用EWS和EpiScan算法可以提高检测敏感性3%,并将误报率降低0.034次/小时。
论文4:
Multivariate Frequency Domain Analysis of Causal Interactions in Physiological Time Series
多变量频域分析在生理时间序列中的因果相互作用
方法
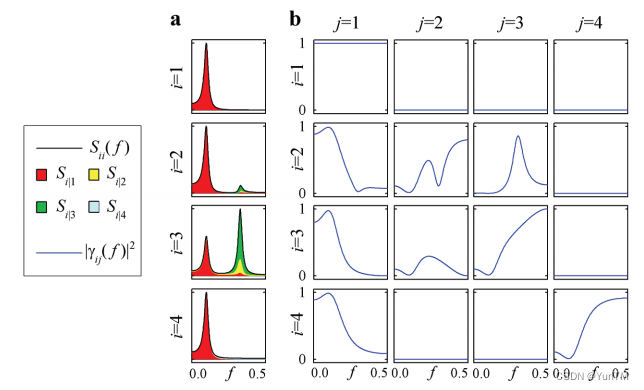
时间序列分析:采用多变量时间序列分析技术,研究动态生理系统中收集的多个信号之间的相互依赖性。
频域表示:利用线性时间序列分析方法,通过频率域表示多通道数据,分析信号间的耦合和因果关系。
Granger因果性:基于Granger因果性的概念,评估多变量过程中的因果关系,即一个过程对另一个过程的影响。
模型系数和谱表示:在多变量自回归(MVAR)模型的框架内,通过模型系数和它们的谱表示来量化耦合和因果关系。
创新点
时间序列分析:采用多变量时间序列分析技术,研究动态生理系统中收集的多个信号之间的相互依赖性。
频域表示:利用线性时间序列分析方法,通过频率域表示多通道数据,分析信号间的耦合和因果关系。
Granger因果性:基于Granger因果性的概念,评估多变量过程中的因果关系,即一个过程对另一个过程的影响。
模型系数和谱表示:在多变量自回归(MVAR)模型的框架内,通过模型系数和它们的谱表示来量化耦合和因果关系。
