基于贝叶斯核张量回归的可扩展时空变系数模型

文章信息

本周阅读的论文是一篇2024年发表在《Bayesian Analysis》上利用贝叶斯核回归技术处理高维时间序列的文章,题目为《Scalable Spatiotemporally Varying Coefficient Modeling with Bayesian Kernelized Tensor Regression》。

摘要

作为空间统计中的一项回归技术,时空变系数模型(STVC)是一项挖掘空间和时间上的非平稳和可解释的协变量关联性的重要工具。然而,由于其高昂的计算消耗,难以将其应用与大规模的时空分析中。为了解决这项挑战,我们拓展STVC模型至一个三维张量框架中,并将时空变系数重构为一个低秩张量回归问题。低秩分解可以有效地对数据集的全局模式进行建模,并且大大减少了参数的数量。为了进一步整合局部时空依赖性,作者在时间和空间因子矩阵上使用高斯过程先验。作者将整个框架成为贝叶斯核张量回归(BKTR),核张量分解是一种具有低秩协方差结构的多变量时空过程建模的新方法。在模型推断方面,作者使用有效的马尔科夫链-蒙特卡罗(MCMC)算法,使用Gibbs采样更新因子矩阵,使用切片采样更新内核超参数。在人工合成和真实世界数据集上的大量实验表明了BKTR在模型估计和参数推断方面的优越性能。

介绍

局部空间回归旨在刻画响应变量与相应协变量在空间中观察到的非平稳性和异质关联性,这是通过假设回归系数随空间局部变化而实现的。局部空间回归提供了复杂关系的可解释性,并已成为地理学、生态学、经济学、环境、公共卫生和气候科学等许多领域的重要技术。通常来说,一个响应变量y的局部空间回归模型可以写成如下所示:
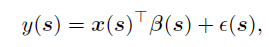
其中,s表示一个空间位置的索引(比如经度和纬度),x(s)和β(s)分别表示位置s上的协变量向量和回归系数,ε(s)表示精度为τ的高斯白噪声过程。该回归模型可以进一步扩展为局部时空回归用以进一步刻画系数的时间变化。对于一个在一系列时间点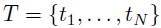 从一系列位置
从一系列位置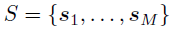 观察到的响应矩阵
观察到的响应矩阵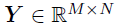 ,定义在笛卡尔积
,定义在笛卡尔积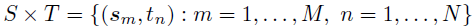 上的局部时空回归模型表示如下:
上的局部时空回归模型表示如下:
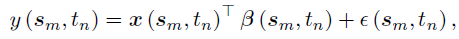
其中,m和n分别表示行和列的索引。在建模上述模型时,参数的更新总是需要大量的计算费用,导致无法在大规模案例中使用。
本文提出一种可选择的估计策略,即贝叶斯核张量回归(BKTR),用以在大规模数据集上进行贝叶斯时空回归分析。受到低秩回归和张量回归的启发,作者使用低秩张量分解编码不同维度的依赖性。为了进一步整合局部空间和时间依赖性,作者对空间和时间因子向量使用高斯过程先验,因此将常规的张量分解转化为核分解模型。假定张量的秩为R,则时间复杂度变为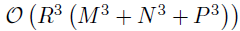 ,大幅降低了时间复杂度。除了空间和时间框架,作者还考虑了响应矩阵Y中有部分元素无法被观察到或者损坏的情况。这类场景在实际应用中十分常见,从新兴的众包和移动传感系统(如Google Waze)收集的交通状态数据,这些系统的观测在空间和时间上本质上是稀疏的。实验结果表明,即使在缺失率很高的情况下,底层的贝叶斯张量分解框架使模型可以有效估计模型系数以及无法观察的数据。
,大幅降低了时间复杂度。除了空间和时间框架,作者还考虑了响应矩阵Y中有部分元素无法被观察到或者损坏的情况。这类场景在实际应用中十分常见,从新兴的众包和移动传感系统(如Google Waze)收集的交通状态数据,这些系统的观测在空间和时间上本质上是稀疏的。实验结果表明,即使在缺失率很高的情况下,底层的贝叶斯张量分解框架使模型可以有效估计模型系数以及无法观察的数据。

贝叶斯核张量分解

模型介绍
令是一个M×N×P的张量,第(m,n)个模-3纤维(mode-3 fiber)是时间和位置上的协变量向量,即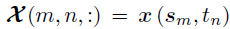 。例如,在共享单车需求的时空建模应用中,响应矩阵
。例如,在共享单车需求的时空建模应用中,响应矩阵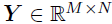 是一个N天内M辆自行车每日出发行程的矩阵,而张量变量
是一个N天内M辆自行车每日出发行程的矩阵,而张量变量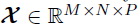 表示对应位置和时间上的P个时空协变量集合。使用
表示对应位置和时间上的P个时空协变量集合。使用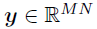 定义 vec(Y),则上述公式可以重新写为:
定义 vec(Y),则上述公式可以重新写为:
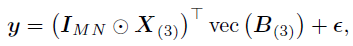
其中,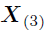 和
和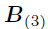 分别是张量和的展开,Khatri-Rao积
分别是张量和的展开,Khatri-Rao积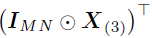 是一个大小为
是一个大小为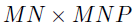 的块对角矩阵,且
的块对角矩阵,且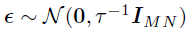 。假设,
。假设,
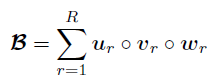
服从一个秩为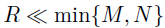 的CP分解,则上式可以重写为,
的CP分解,则上式可以重写为,
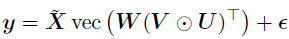
其中,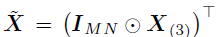 表示一个扩展协变量矩阵,该公式的参数量为R(M+N+P),远低于没有使用CP分解情况下的参数量(MNP)。
表示一个扩展协变量矩阵,该公式的参数量为R(M+N+P),远低于没有使用CP分解情况下的参数量(MNP)。
局部空间和时间处理对于建模时空数据是非常重要的。然而,仅靠低秩假设无法编码这种局部依赖性。为了解决这个问题,作者按照GP因素分析策略假设U和V的特定高速过程先验,对W使用一个共轭正态先验,接着提出一个全贝叶斯方法以估计上述模型。图1展示了文章所提出的模型框架,成为贝叶斯核张量回归(BKTR),其图形模型如图2所示。
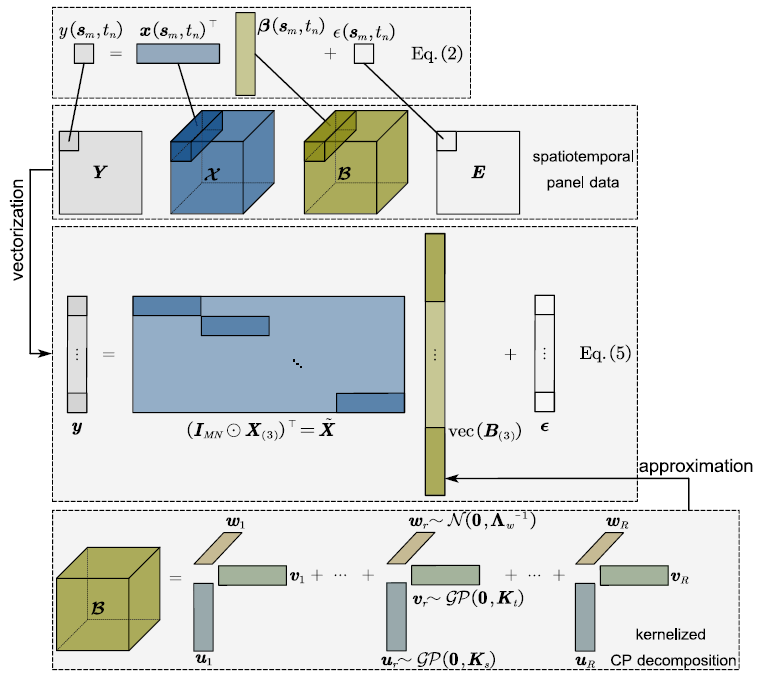
图1:BKTR框架计算示意图
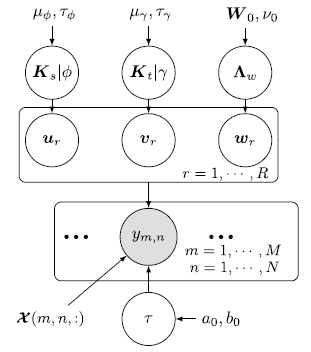
图2:BKTR的图模型
在实际应用中,依赖数据通常只有部分可以被观察,这部分数据的集合被定义为集合,且满足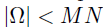 。作者定义D作为0-1指示矩阵,如果
。作者定义D作为0-1指示矩阵,如果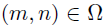 ,则
,则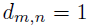 ;否则
;否则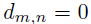 。是一个大小为
。是一个大小为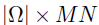 的指示矩阵,通过从一个
的指示矩阵,通过从一个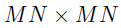 指示矩阵中删除掉vec(D)中0值所在的行所获得,那么观测数据向量可以通过
指示矩阵中删除掉vec(D)中0值所在的行所获得,那么观测数据向量可以通过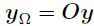 获得,进一步的,
获得,进一步的,
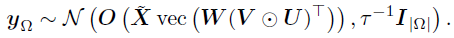
对于空间和时间因子矩阵U和V,作者在向量的分量上分别使用相同的GP先验:
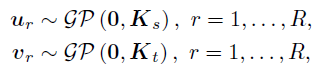
其中,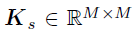 和
和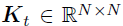 分别是从两个有效核函数
分别是从两个有效核函数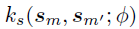 和
和 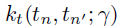 中构建的空间和时间协方差矩阵,其中和是核函数的长度-尺度超参数。需要注意的是,作者通过W捕捉方差,因此通过将方差设置为1从而限制和为相关矩阵。另外,作者将核超参数重新参数化为对数变换变量以确保参数的非负性并假设它们的先验服从正态分布,即
中构建的空间和时间协方差矩阵,其中和是核函数的长度-尺度超参数。需要注意的是,作者通过W捕捉方差,因此通过将方差设置为1从而限制和为相关矩阵。另外,作者将核超参数重新参数化为对数变换变量以确保参数的非负性并假设它们的先验服从正态分布,即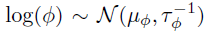 和
和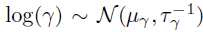 。对于因子矩阵W,假设所有列服从一个相同的零均值高斯分布,其中精度矩阵服从Wishart共轭先验:
。对于因子矩阵W,假设所有列服从一个相同的零均值高斯分布,其中精度矩阵服从Wishart共轭先验:
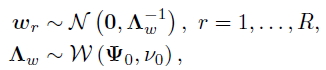
其中,是一个的正定尺度矩阵,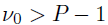 表示自由度。最后,在噪声精度上使用共轭伽马先验
表示自由度。最后,在噪声精度上使用共轭伽马先验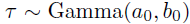 。
。
基于上述先验和超先验,可以写出BKTR中的系数的协方差函数。具体来说,考虑两个数据对,分别是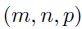 和
和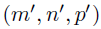 ,那么这两个数据对之间的协方差如下,
,那么这两个数据对之间的协方差如下,
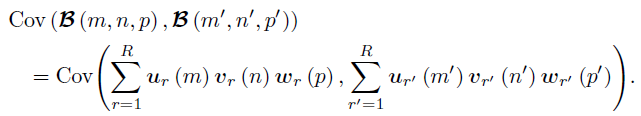
给定的先验,则有,
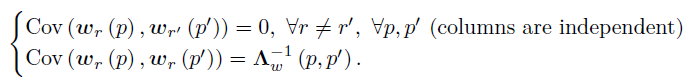
结合上述协方差公式,可得,
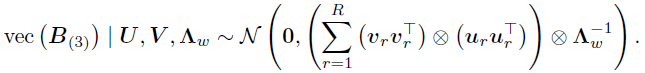
相同的,如果边缘U,则可以推出,
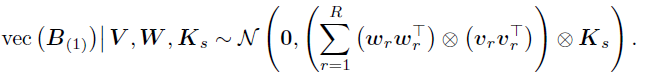
模型推断
作者采用Gibbs采样来估计模型参数,包括系数因子{U,V,W},精度τ,以及精确度矩阵。对于核超参数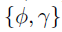 ,由于条件分布不容易采样获得,因此使用slice sampler。
,由于条件分布不容易采样获得,因此使用slice sampler。
1. 采样系数因子{U,V,W}
采样因子矩阵可以视为一个贝叶斯线性回归问题。以W为例,可以得到下式,
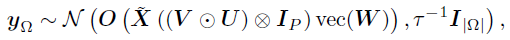
其中,U和V已知,vec(W)是需要估计的系数。考虑到每个成分向量的先验是独立且相同的,那么整个向量化的W的先验分布可以写成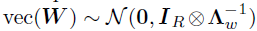 。由于
。由于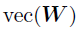 的先验和似然均服从高斯分布,因此其后验也服从高斯分布,其中精度和均值如下:
的先验和似然均服从高斯分布,因此其后验也服从高斯分布,其中精度和均值如下:
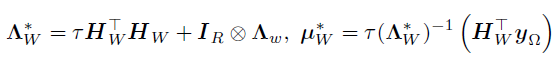
其中,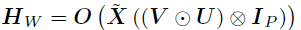 ,大小为
,大小为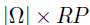 。U和V的后验分布可以使用不同的张量展开所获得。为了对U进行采样,使用mode-1展开,并使用vec(U)重构回归模型如下:
。U和V的后验分布可以使用不同的张量展开所获得。为了对U进行采样,使用mode-1展开,并使用vec(U)重构回归模型如下:
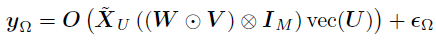
其中,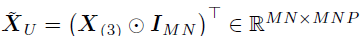 ,
,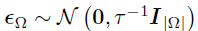 。因此,vec(U)的后验存在一个闭合形式——高斯分布,其精度和均值分别如下
。因此,vec(U)的后验存在一个闭合形式——高斯分布,其精度和均值分别如下
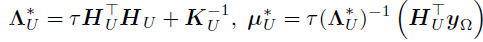
其中,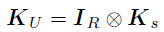 ,
,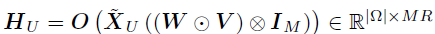 。关于vec(V)的后验可以通过应用mode-2的张量展开来获得。上述的推导为整个因子矩阵提供了后验,即
。关于vec(V)的后验可以通过应用mode-2的张量展开来获得。上述的推导为整个因子矩阵提供了后验,即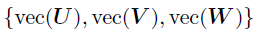 ,因此时间复杂度为
,因此时间复杂度为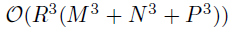 。
。
2. 采样核超参数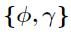
如图2所示,通过Metropolis-Hastings算法,在因子矩阵的条件下采样核超参数应该是简单的。然而,实际中,在这种分层的GP模型中,以潜在变量{U,V}为条件通常会引起后验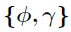 的急剧峰值,使马尔可夫链混合缓慢,导致更新不良。为了解决这个问题,作者从模型中积分出潜在因素得到边际似然,并基于切片采样法从他们的边际后验分布中采样
的急剧峰值,使马尔可夫链混合缓慢,导致更新不良。为了解决这个问题,作者从模型中积分出潜在因素得到边际似然,并基于切片采样法从他们的边际后验分布中采样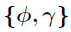 ,即在推导边际后验
,即在推导边际后验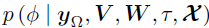 时对U进行积分;同样,通过对V积分从而推导边际后验
时对U进行积分;同样,通过对V积分从而推导边际后验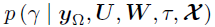 。以的超参数为例,令
。以的超参数为例,令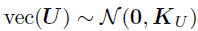 ,其中
,其中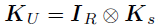 ,对
,对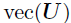 进行积分,可以获得:
进行积分,可以获得:
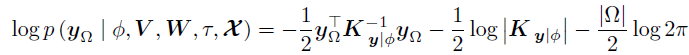
其中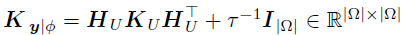 以及
以及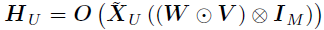 。则的边际后验为:
。则的边际后验为:
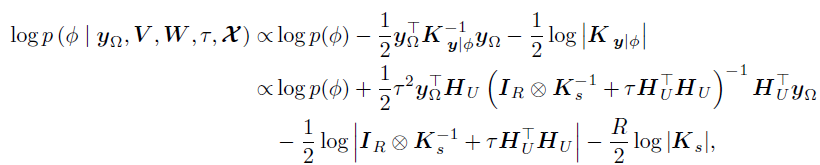
切片采样方法对采样尺度的选择具有鲁棒性,且易于实现。采样可以采用相近的方式。需要注意的是,采样是在对数转换的变量上执行的,以避免数值问题。
3. 采样
给定共轭Wishart先验,的后验分布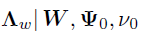 是
是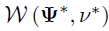 ,其中
,其中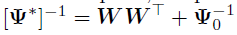 ,且
,且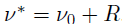 。
。
4. 采样精度τ
由于文章使用了共轭Gamma先验,τ的后验分布仍然是一个Gamma分布,其形状和速率分别是,
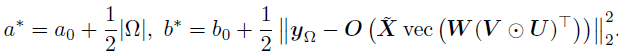
模型实现
BKTR的实现过程如算法1所示。具体来说,将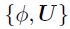 视为一个块,并从的后验分布中通过切片采样对其进行更新,接着从
视为一个块,并从的后验分布中通过切片采样对其进行更新,接着从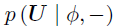 中更新U。相似的操作同样用于采样
中更新U。相似的操作同样用于采样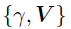 。对于MCMC推断,模型首先经过K1次迭代热启动,然后接下来的K2次迭代的结果作为估计值。
。对于MCMC推断,模型首先经过K1次迭代热启动,然后接下来的K2次迭代的结果作为估计值。

模型扩展性
与原始的STVC相比,BKTR大幅降低了在更新超参数方面需要的计算量,更新因子矩阵U需要 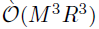 的时间,对于超参数的切片采样,切片采样循环内的每次更新需要
的时间,对于超参数的切片采样,切片采样循环内的每次更新需要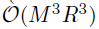 的时间在计算似然函数。这样在计算时间上的巨大收益使模型能够分析大规模的现实世界时空数据和多维关系,而通常STVC是不可行的。
的时间在计算似然函数。这样在计算时间上的巨大收益使模型能够分析大规模的现实世界时空数据和多维关系,而通常STVC是不可行的。
基于上述的分析,BKTR的计算成本依赖于秩R,且BKTR可以在大规模数据集上使用,比如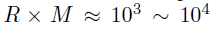 。但是,应该注意的是,默认的BKTR在空间位置的数量M或者时间点N变得很大时(比如,M大于104)仍然会遇到计算问题。最常见的解决方案是按列更新三种因子矩阵,可以减少时间消耗至
。但是,应该注意的是,默认的BKTR在空间位置的数量M或者时间点N变得很大时(比如,M大于104)仍然会遇到计算问题。最常见的解决方案是按列更新三种因子矩阵,可以减少时间消耗至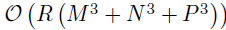 。通过这个更新方案,可以避免使用Kroneceker乘积学习潜在因子和超参数。另外,还可以使用稀疏近似和预测过程去建模每个潜在因子向量,即使用M0个推断点,其中M0<<M,那么时间复杂度降为
。通过这个更新方案,可以避免使用Kroneceker乘积学习潜在因子和超参数。另外,还可以使用稀疏近似和预测过程去建模每个潜在因子向量,即使用M0个推断点,其中M0<<M,那么时间复杂度降为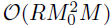 。最后,考虑到通过切片采样学习超参数是昂贵的,进一步降低计算成本的另一种可能的解决方案是使用交叉验证来指定核超参数。核超参数的选择在回归中通常不是敏感的,因此交叉验证可以在适度粗糙的分辨率下进行。然而,直接实现基于MCMC采样的交叉验证方法仍然很耗时,因为这种迭代过程需要对每个超参数组合运行几次。
。最后,考虑到通过切片采样学习超参数是昂贵的,进一步降低计算成本的另一种可能的解决方案是使用交叉验证来指定核超参数。核超参数的选择在回归中通常不是敏感的,因此交叉验证可以在适度粗糙的分辨率下进行。然而,直接实现基于MCMC采样的交叉验证方法仍然很耗时,因为这种迭代过程需要对每个超参数组合运行几次。

实验研究

文章在三个仿真数据集上进行了实验来测试BKTR的性能。具体来说,进行了以下三个研究:(1)一个低秩结构化关联分析,用以检验不同秩设置和不同观测/缺失率场景下BKTR的估计精度和统计特性;(2)小规模分析,用以比较BKTR和STVC以及一个纯低秩张量回归模型;(3)中等规模分析,用以测试BKTR在更在使用的STVC建模上的性能。感兴趣的读者可以阅读原文实验部分。

结论

本文引入了一个有效的解决大规模局部时空回归分析的方法。作者提出使用低秩CP分解用以参数化模型系数,有效地将参数数量由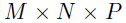 降低至
降低至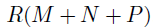 。与现有张量回归的研究不同,提出的模型BKTR通过整合GP先验去刻画较强的局部空间和时间依赖性,从而超越了低秩假设。框架同样学习了一个低秩多线性核,该核具有表现力,能够为非平稳和复杂过程提供见解。在虚拟和真实的数据集上的数值实验表明BKTR能够高效、可靠地再现局部时空过程。
。与现有张量回归的研究不同,提出的模型BKTR通过整合GP先验去刻画较强的局部空间和时间依赖性,从而超越了低秩假设。框架同样学习了一个低秩多线性核,该核具有表现力,能够为非平稳和复杂过程提供见解。在虚拟和真实的数据集上的数值实验表明BKTR能够高效、可靠地再现局部时空过程。
