- 将广义线性模型的联系函数选择为类别函数，即找一个单调可微函数将分类任务的真实标记y与线性回归模型的预测值联系起来，即可以用于做分类预测。
- ”单位阶跃函数“（unit-step function）是一种典型的二分类函数，但它不连续。
- ”对数几率函数“（logsitic function）是常用的近似单位阶跃函数的”替代函数“（surrogate function），对数几率函数也叫”对率函数“。
- 对数几率函数的形式：
，最终的形式为：
- 对数几率函数是一种”Sigmoid“函数。Sigmoid函数术形状像S的函数，对率函数是其典型代表。
- 对数几率回归（logistic regression，也叫 logit regression），在有的文献中翻译为“逻辑回归”（印象中不少），在西瓜书中，周老师认为中文”逻辑“与”logistic“ 和”logit“的真实含义不对等，因此意译为”对数几率回归“，也称为”对率回归“。
- 对数几率回归是做分类的。虽然名称叫回归，实际上是分类学习算法。
- 以二分类看，将y记做正例的可能性，那么1-y就可以记作反例的可能性，两者的比值
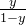成为”几率“（odds），反映了作为正例的相对可能性。 - 对几率取对数，得到”对数几率“（log odds，也叫 logit），格式为
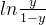。 - 由于正例、反例的概率不全是0和1，因此对数几率取得的值是很多的，它不是仅仅预测出”类别“，而且能得到近似概率预测，这对许多需要应用概率辅助决策的任务很有用。
- 对率回归直接对分类可能性建模，无需事先假设数据分布，避免了假设分布不准确所带来的问题。
- 对率回归求解的目标函数是任意阶可导的凸函数。
- 可以通过”极大似然法“（maximum likelihood method）来估计参数。
- 很多数值优化算法都可以直接用于求解最优解。（!!!有点超纲了!!!）属于最优化问题中的”无约束优化问题“。
- 经典的数值优化算法有梯度下降法（gradient descent method）、牛顿法（Newton method）。
- 梯度下降法是一种迭代求解算法。
- 基本思路：先在定义域中随机选取一个点x0，代入函数后判断f(x0)是否是最小值，如果不是则找下一个点x1，且保证f(x1)
- 利用”梯度指向的方向是函数值增大速度最快的方向“这一特性，没次迭代时沿着梯度反方向进行，进而实现迭代值越来越小。
- 梯度下降设置的参数有α，称为“步长”或“学习率”。
- 为了防止迭代无休止进行，通常还会设置一个极小阈值ε，当某次迭代造成的函数值波动小于这个值时，近似地认为已经取到了最小值。
- 牛顿法和梯度下降法基本思路一致。差别在在取下一个点时：
- 梯度下降法只要求通过泰勒公式在当前点的邻域内找到一个函数值更小的点。
- 牛顿法期望下一个点是当前点的邻域内的极小值。
