概率论之常见分布与matlab绘图

1.二项分布

1.1基本形式

$$\mathrm{X}\sim \mathrm{B}\left(\mathrm{n},\mathrm{p}\right)$$

1.2概率公式

$$\mathrm{P}\left(\mathrm{x}=\mathrm{k}\right)={\mathrm{C}}_{\mathrm{n}}^{\mathrm{k}}{\mathrm{p}}^{\mathrm{k}}{\left(1-\mathrm{p}\right)}^{\mathrm{n}-\mathrm{k}}$$

1.3概率密度函数

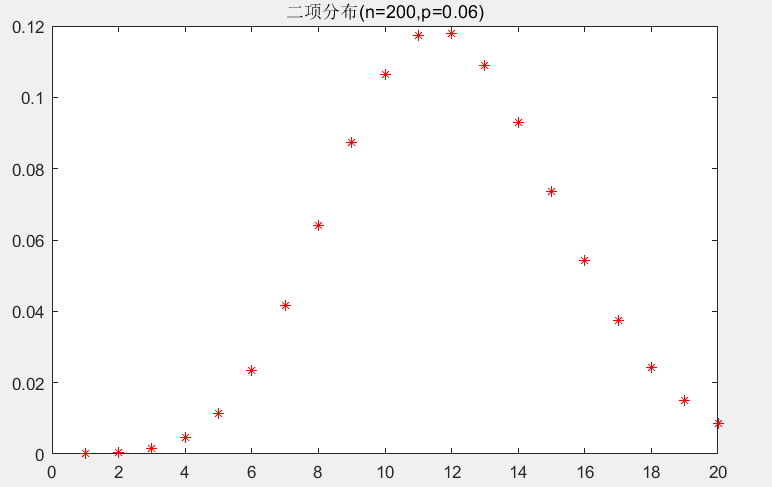
1.4matlab代码

clear;
clc;
x=1:20;
y=binopdf(x,200,0.06);
figure;
plot(x,y,'r*');
title('二项分布(n=200,p=0.06)');

1.5我的理解

在这个二项分布的两个参数里面，这个第一个参数表示的就是我们的这个实验的进行的次数，第二个参数表示的就是我们的这个对应的某一个事件出现的这个概率；

结合实际的情景进行理解这个二项分布：

在医学实验中，比如测试某种新药物的疗效。可以把对每个患者使用药物看作是一次独立试验，药物对患者有效的概率设为p ，选取n个患者参与实验。通过二项分布，就能知道在这n个患者里，有多少患者能达到预期疗效（比如恰好有k个患者病情好转）的概率情况。这对于评估药物的有效性、决定是否继续研发推广该药物等起着关键作用。（来自AI，只会为了更好地理解这个理论在我们的生活里面的应用，方便我们的这个学习理解）；

在上面的这个案例里面，我们就是通过这个二项分布对于我们的这个药物的效果进行预测，当真实的情况发生之后，我们就可以进行核对，校验这个药物的有效性；

2.泊松分布

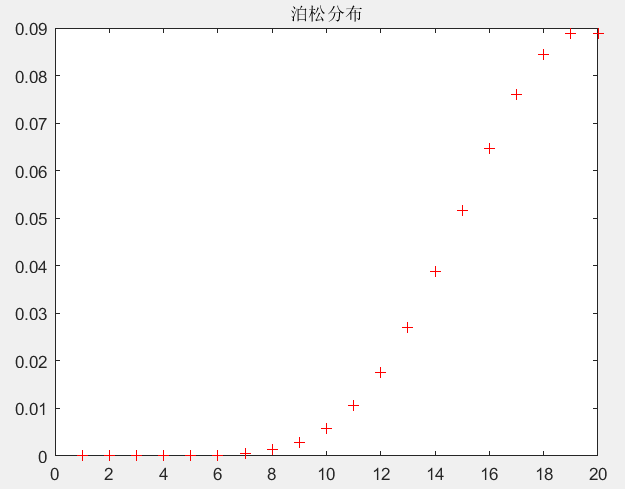
2.1基本绘图

clear;
clc;
x=1:20;
y=poisspdf(x,20);
figure;
plot(x,y,'r+')
title('泊松分布')

2.2高级绘图

lambda_values = [1, 3, 5, 10];
x = 0:19; % 定义取值范围

for lambda_val = lambda_values
    y = poisspdf(x, lambda_val); % 计算泊松分布概率质量函数值
    plot(x, y, 'o-', 'DisplayName', sprintf('lambda = %d', lambda_val));
    hold on;
end
xlabel('k (Number of events)');
ylabel('Probability');
title('Poisson Distribution Probability Mass Function');
legend('show');

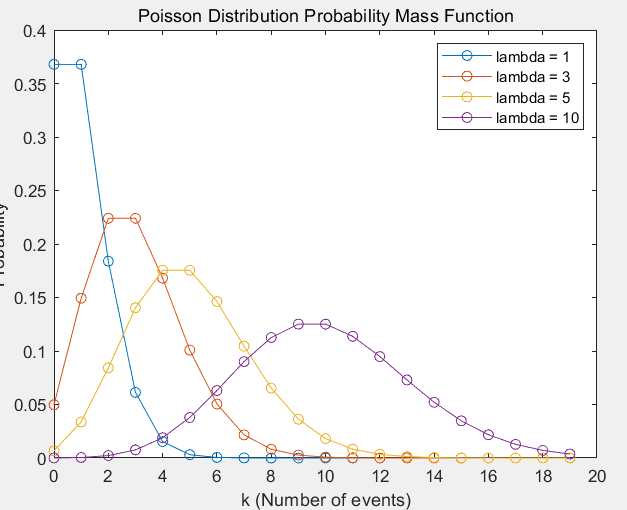
2.3一点说明

我们上面介绍的这个二项分布，在这个n很大的时候就是趋近于这个泊松分布的；

3.指数分布

3.1计算方法

$$\mathrm{f}\left(\mathrm{x}\right)=\{{}_{0,\mathrm{else}}^{{}^{{\lambda \mathrm{e}}^{-\lambda \mathrm{x}},\mathrm{x}>0,\lambda >0}}$$

3.2图像绘制

clear;
clc;
x=0:0.1:10;
y=exppdf(x,2);
figure;
plot(x,y,'r:');
title('指数分布')

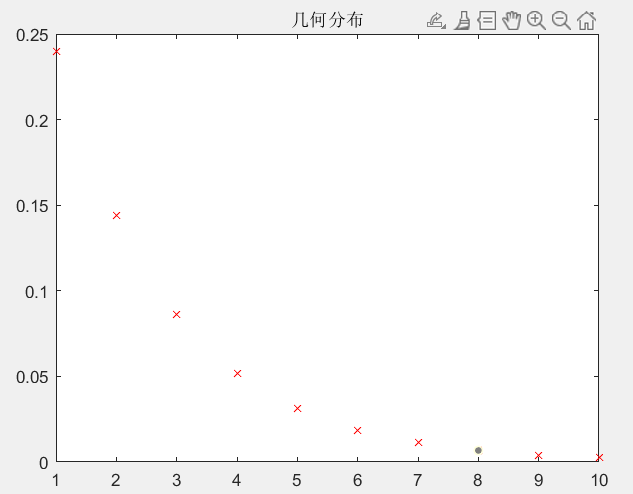
4.几何分布

4.1计算方法

p { x = k } = ( 1 − p ) k − 1 p \mathrm{p}\left\{ \mathrm{x}=\mathrm{k} \right\} =\left( 1-\mathrm{p} \right) ^{\mathrm{k}-1}\mathrm{p} p{x=k}=(1−p)k−1p

4.2绘图代码

clear;
clc;
x=1:10
y=geopdf(x,0.4)
figure;
plot(x,y,'rx');
title('几何分布')