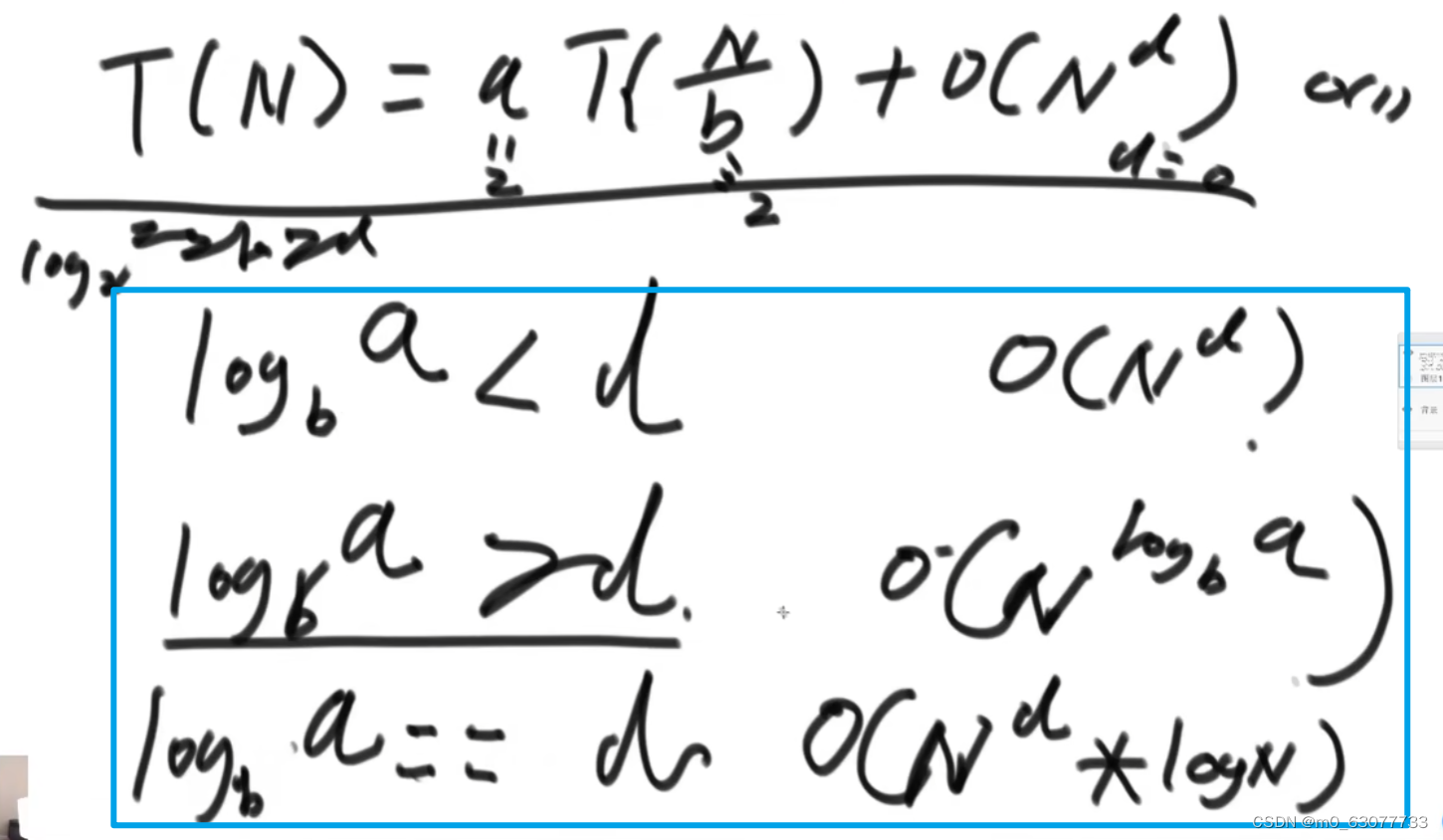复杂度和简单排序算法【左程云:Java】
目录
1.常见的常数时间操作
2.选择排序
3.冒泡排序
编辑
4.位运算----异或运算【相同为0,不同为1==无进位相加】
编辑
异或的性质
使用异或前的条件:【a,b在内存独立】
异或:可以用于交换两个变量的值
练习1:
编辑
练习2:
如何去除最右侧第一个不等于0的数值
5.插入排序
6.时间复杂度
7.时间复杂度的意义
8.二分查找法
一、在一个有序的数组中查找是否有某一个数的存在
时间复杂度
二、在一个有序数组中,找>=某一个数最左侧的位置
3.局部最小值问题
局部最小的定义
9.对数器
一、对数器的概念
10.递归行为和递归行为时间复杂度
1.使用递归找到数组中最大值
int mid=L+((R-L)>>1)
2.mster公式
1.常见的常数时间操作


2.选择排序



public class S01_Selectsort {
public static void selectionSort(int[] arr){
if(arr===null || arr.length<2){
return;
}
//0 - N-1
//1 - N-2
//2 - N-3
for(int i=0;i<arr.length-1;i++){
// 最小值在哪一个位置上:i~n-1
int minIndex=i;
// j默认比i大1,一开始从第二个数开始查找
for(int j=i+1;j<arr.length;j++){
minIndex=arr[j]<arr[minIndex]?j:minIndex;
}
swap(arr,i,minIndex);
}
}
public static void swap(int[] arr,int i,int j){
int temp=arr[i];
arr[i]=arr[j];
arr[j]=temp
}
}



3.冒泡排序

冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。 它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。 这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
public class Code02_BubbleSort {
public static void bubbleSort(int[] arr){
if(arr ==null || arr.length <2){
return;
}
//0~N-1
//1~N-2
//2~N-3
// 因为比较后都是将最大值放在最后,所以使用arr.length-1
for(int e=arr.length-1;e>0;e--){
// 比较索引值上的值
// 0 1
// 1 2
// 2 3
// e-1 e
for(int i=0;i<e;i++){
if(arr[i]>arr[i+1]){
swap(arr,i,i+1);
}
}
}
}
// 交换arr的i和j位置上的值
public static void swap(int[] arr,int i,int j){
arr[i]=arr[i]^arr[j]
arr[j]=arr[i]^arr[j]
arr[i]=arr[i]^arr[j]
}
}
4.位运算----异或运算【相同为0,不同为1==无进位相加】
异或操作性质:一个数与自身异或=自身
异或的性质

使用异或前的条件:【a,b在内存独立】
a,b在内存独立,不能是同一个引用对象
异或:可以用于交换两个变量的值

public class Test {
public static void main(String[] args) {
int a = 7;
int b = 4;
int c = a^b;
int d = a^b^a;
System.out.println(c); //3
System.out.println(d); //4
}
}
练习1:
1)数组中,一个数出现了奇数次,其他数出现了偶数次,要找奇数次的数
答案:将所有数都异或,最后只剩下奇数次的数。
异或运算只和数据的个数有关,和顺序无关



public static void printOddTimesNum1(int[] arr) {
int eO = 0;
for (int cur : arr) {
eO ^= cur;
}
System.out.println(eO);
}练习2:
数组中,2个数a,b出现了奇数次,其他数出现了偶数次,要找奇数次的数
答案:将所有数都异或,得到eor=a异或b;因为a!=b,所以eor!=0,必造成eor有一个位上为1,那个位就能用来区分a和b。


如何去除最右侧第一个不等于0的数值
&:含0得0,全1为1

int rightOne=eor &(~eor+1);偶数位数组,第一次结果得到的是a∧b,再用一次异或结果是a or b
public static void printOddTimesNum2(int[] arr) {
int eO = 0, eOhasOne = 0;
for (int i0;i<arr.length;i++) {
eO ^= arr[i];
}
int rightOne = eO & (~eO + 1);//选出e0最右边的一个1,
for (int cur : arr) {
if ((cur & rightOne) != 0) {
eOhasOne ^= cur;//最后得到的这个数,是这一个位上有1的数,与其他数的异或
}
}
System.out.println(eOhasOne + " " + (eO ^ eOhasOne));
}5.插入排序



public static void insertionSort(int[] arr){
if(arr==null|| arr.length<2){
return;
}
//0-0 有序的
//0-i 想有序
// 当前最大的下标值
for(int i=1;i< arr.length;i++){
// 判断在0~i之间是否有值比arr[i]这个位置上的数值大,要是大则进入这个for
for(int j=i-1;j>=0 && arr[j]>arr[j+1];j--){
// j--:不断的往前进行比较
swap(arr,j,i);
}
}
}
public static void swap(int[] arr,int i,int j){
arr[i]=arr[i]^arr[j];
arr[j]=arr[i]^arr[j];
arr[i]=arr[i]^arr[j];
}6.时间复杂度

7.时间复杂度的意义

8.二分查找法
不是有序才可以二分查找
一、在一个有序的数组中查找是否有某一个数的存在

2分找到数就停止。
时间复杂度

二、在一个有序数组中,找>=某一个数最左侧的位置

2分找到数,还要继续,直到最左侧停止
3.局部最小值问题
局部最小的定义


用的是零点定理的思想,上图中,3个位置的趋势,左边两个趋势,中间必有最小值。
9.对数器
一、对数器的概念

算法c是自己写的,算法b是系统提供的排序算法,使用随机数组,2种算法对比,看c是否有错。
public static void comparator(int[] arr) {
Arrays.sort(arr);
}10.递归行为和递归行为时间复杂度

1.使用递归找到数组中最大值
int mid=L+((R-L)>>1)


public static int getMax(int[] arr){
return process(arr,0, arr.length-1);
}
// arr[L...R]范围上求最大值
public static int process(int[] arr,int L,int R){
if(L==R){
// arr[L...R]范围只有一个数,直接返回
return arr[L];
}
// 中点
int mid=L+((R-L)>>1);
int leftMax=process(arr,L,mid);
int rightMax=process(arr,mid+1,R);
return Math.max(leftMax,rightMax);
}2.mster公式
使用此公式的前提是子问题的规模要一致。