Matlab|计及调峰主动性的风光水火储多能系统互补协调优化调度

目录

1 主要内容

2 重点难点解析

3 部分程序

4 程序结果

5 下载链接

1 主要内容

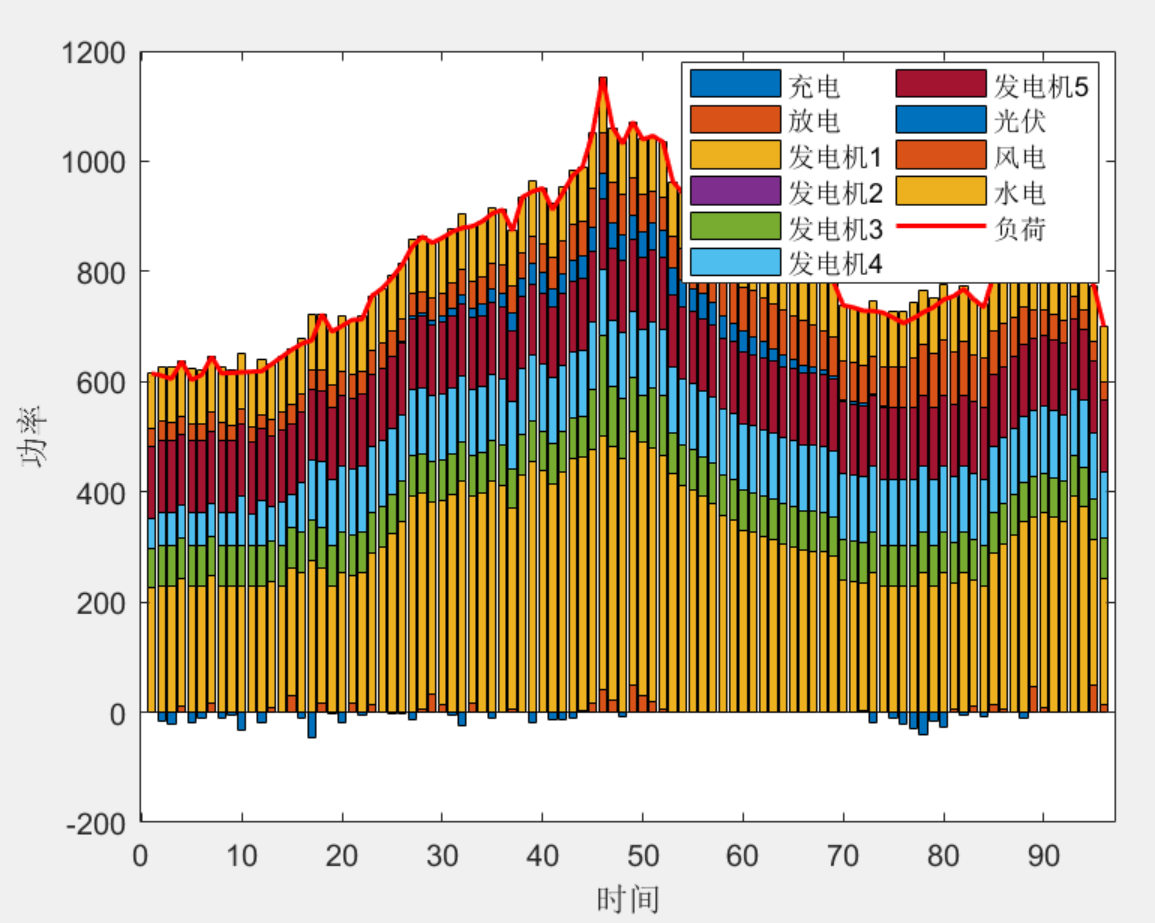
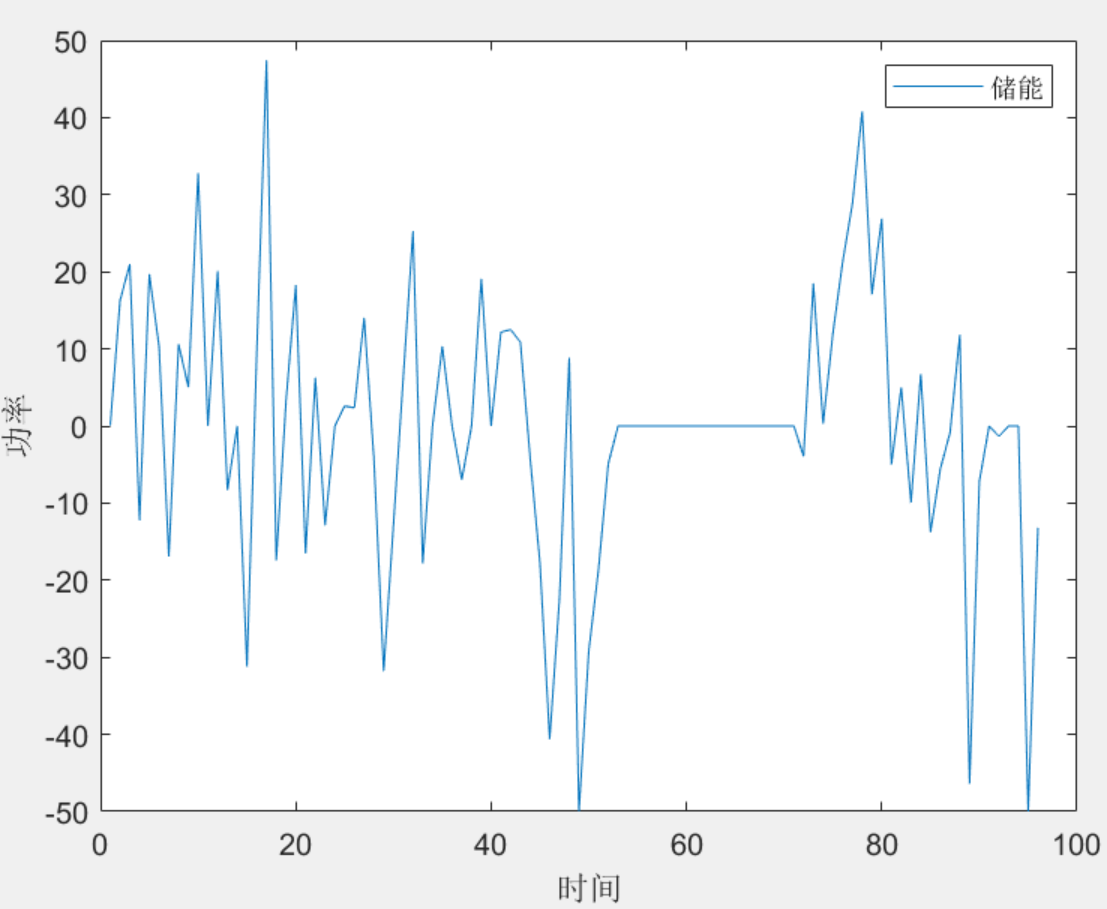
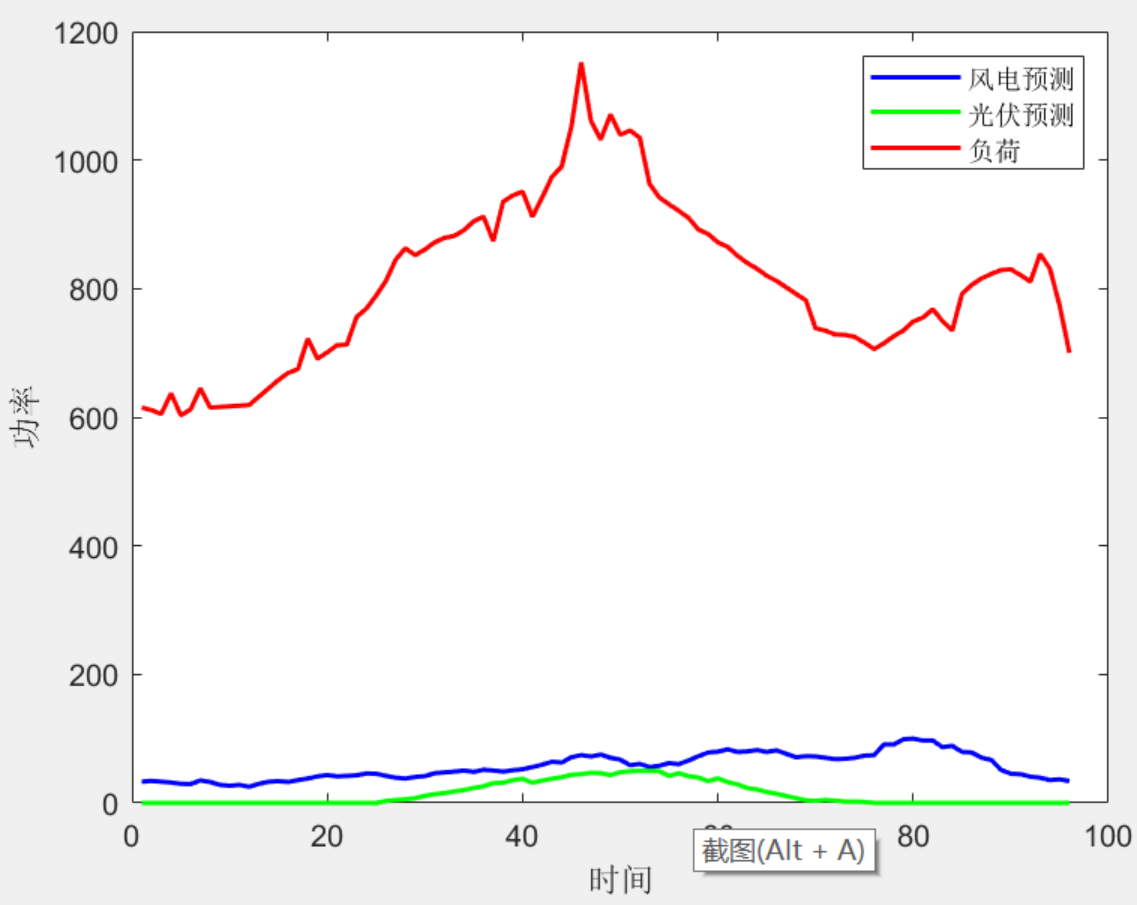
该程序方法复现了《计及调峰主动性的风光水火储多能系统互补协调优化调度》_李铁，考虑多能系统电源结构复杂，涉及变量及约束条件较多，因此采用分层优化调度方案。上层模型以净负荷波动最小和储能系统运行收益最大为优化目标，旨在充分利用储能装置削峰填谷特性，降低负荷峰谷差，提高可再生能源的消纳空间；下层模型以火电机组运行成本最小和可再生能源弃电量最小为优化目标，考虑调峰主动性约束，旨在充分发挥火电机组深度调峰能力，优化可再生能源消纳能力和火电机组经济运行。

2 重点难点解析

很多同学询问过深度调峰机组损耗成本计算的问题，模型见下图。

文章对这部分介绍一笔带过，很多文献都这样，看下面这个：

摘自《考虑广义储能与火电联合调峰的日前–日内 两阶段滚动优化调度》

这里给出了N(P)的公式，是个一元三次函数，且N(P)在分母的地方，可见这里线性化处理的难度。

摘自《计及调峰影响系数的费用分摊及随机经济调度》

在这里也就是一个建模，并没有深入分析该怎么处理，后文甚至对平方项的线性化专门引用文献进行说明，但是这么复杂的线性化过程不该详细分析一下吗？

重点来了，这里的线性化处理是这样的：

按照《一种火电机组调峰能耗成本计算方法》理论，机组损耗成本可以转化为下面的公式。

这个公式里面，d为寿命损耗率，也是求解的关键因素，d可用下面的表中数据进行表示。

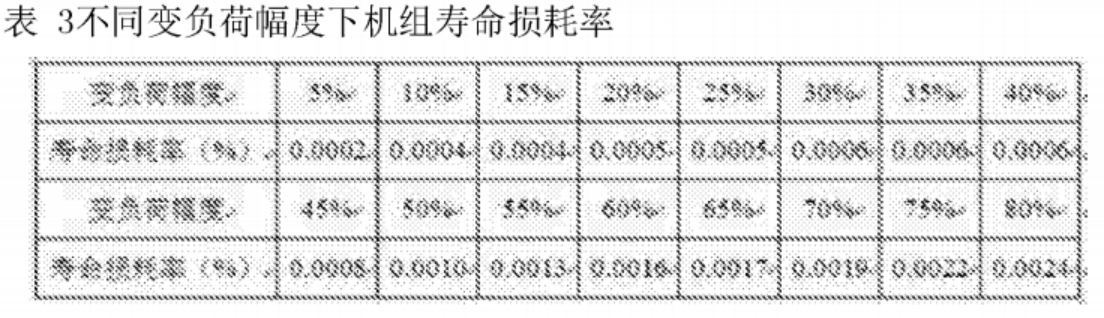
这两部分结合就能把原理复杂非线性的过程转化为分段一次函数的优化过程，求解就方便很多了。

3 部分程序

%% 决策变量
x_theta = sdpvar(nbus, Horizon,'full');%直角潮流相角
x_P_grid = sdpvar(1, Horizon,'full');
x_P_g = sdpvar(ngen, Horizon,'full');%发电机
x_P_ch = sdpvar(nees, Horizon);%蓄电池
x_P_dis = sdpvar(nees, Horizon);%蓄电池
x_P_w = sdpvar(nw, Horizon,'full');%风电
x_P_v = sdpvar(nv, Horizon,'full');%光伏
x_u_g = binvar(ngen, Horizon,'full');%发电机状态
x_u_ch = binvar(nees, Horizon);%蓄电池状态，下同
x_u_dis = binvar(nees, Horizon);
x_P_sg=sdpvar(1, Horizon,'full');%水电
gn=5;%分段函数线性化，下同
x_pf=sdpvar(ngen, Horizon,'full');
gw1=sdpvar(gn+1,Horizon,'full');
gw2=sdpvar(gn+1,Horizon,'full');
gw3=sdpvar(gn+1,Horizon,'full');
gw4=sdpvar(gn+1,Horizon,'full');
gw5=sdpvar(gn+1,Horizon,'full');
gw6=sdpvar(gn+1,Horizon,'full');
gz1=binvar(gn, Horizon,'full');gz2=binvar(gn, Horizon,'full');gz3=binvar(gn, Horizon,'full');gz4=binvar(gn, Horizon,'full');gz5=binvar(gn, Horizon,'full');
%% 约束条件生成
cons = [];
% DG
Pmax = [460;300;243;120;130];%最大发电功率
Pmin = 0.5.*Pmax;%最小发电功率
rg = 0.5.*Pmax;%爬坡
Pa=0.45.*Pmax;
Pb=0.3.*Pmax;
Psmax=100;%水电机组
Psmin=0;
cons_gen = getConsGen1(x_P_g, x_u_g, Pmax, Pb, rg,ru, Horizon);%发电机约束
 cons_sgen = getConssGen(x_P_sg, Psmax, Psmin, Horizon);%水电约束
 cons = [cons, cons_gen,cons_sgen];
% EES
EESmax = 50;
EESmin = 0;
capmax = 300;
re = 0.2;
 cons_ees = getConsEES(x_P_ch, x_P_dis, x_u_ch, x_u_dis, EESmax, EESmin, capmax, re, Horizon);
 cons = [cons, cons_ees];
% PV、Wind约束
PV = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,22.5000000000000,33.7500000000000,40.5000000000000,54,81,99,112.500000000000,130.500000000000,146.250000000000,171,189,225,229.500000000000,258.750000000000,274.500000000000,229.500000000000,254.250000000000,274.500000000000,292.500000000000,319.500000000000,326.250000000000,342,337.500000000000,315,348.750000000000,360,364.500000000000,364.500000000000,360,306,337.500000000000,303.750000000000,288,247.500000000000,279,236.250000000000,211.500000000000,168.750000000000,153,123.750000000000,103.500000000000,78.7500000000000,54,29.2500000000000,24.7500000000000,33.7500000000000,27,15.7500000000000,15.7500000000000,11.2500000000000,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0];
PV=PV./max(PV)*50;
Wind = [80,83,80,77,72,71,85,79,68,65,68,61,72,80,82,79,86,92,100,105,100,102,104,111,110,102,95,92,98,101,112,115,118,122,117,125,122,118,123,127,135,144,155,152,172,180,175,182,170,163,142,147,135,140,150,146,160,176,190,193,202,192,194,199,192,198,185,172,176,175,170,165,166,170,178,180,220,220,240,242,235,235,210,215,192,190,170,162,124,110,108,99,95,86,89,82];
PW=Wind./max(Wind)*100;
 cons_re = getConsRE(x_P_w, x_P_v, PV, PW);
 cons = [cons, cons_re];
 % 潮流约束
 cons_eq = getConsEQ(x_P_grid, x_P_g,x_P_sg, x_P_ch, x_P_dis, x_P_w, x_P_v, L_Horizon, caseName, x_theta, igd, idg, ie, iw, iv,is); %直流潮流模式
 cons = [cons, cons_eq];
% % 线路传输约束
  [cons_pf, pf] = getConsPF(caseName, x_theta, Horizon);
  cons = [cons, cons_pf];
  cons = [cons, getConsAgl(x_theta)];
%分段线性化

程序采用模块化编程方式，方便理解和调试，因此下载之后很多子函数无法单独运行，需要经过主程序调用才可运行！

4 程序结果

5 下载链接