【优先算法】专题——双指针

1.移动零

移动零

题目描述：

思路：

本题我们把数组分块，将非零元素移动到左边，为零元素移动右边。

我们使用双指针算法（利用数组下标来充当指针）

两个指针的作用：

cur：从左往右扫描数组，遍历数组

dest：已经处理的区间内，非零元素的最后一个位置

我们将数组分为三个区间：

如何做到：

cur从前往后遍历的过程中：

1,遇到0元素：cur++;

2.遇到非零元素：

• swap(dast+1,cur);
• dest++，cur++;

参考代码如下：

class Solution {
public:
    void moveZeroes(vector<int>& nums) 
    {
        int cur = 0;
        int dest = -1;
        while(cur < nums.size())
        {
            
           if(nums[cur] == 0)
            {
                ++cur;
            }
            else
            {
                swap(nums[cur],nums[dest+1]);
                ++cur;
                ++dest;
            }
        }
    }
};

这个题其实我们用到了快排的思想

2.复写零

复写零

题目描述：

题目分析：题目说不要超过数组长度其实就是告诉我们不要越界，题目还告诉我们不能创建额外数组让我们就地修改原数组，我们不需要返回任何内容。

思路：我们依旧使用双指针算法，先根据“异地”操作，然后优化成双指针下的“就地”操作

1.先找到最后一个复写的数

• 先判断cur位置的值
• 决定dest向后移动一步或者两步
• 判断一下dest是否已经到结束为止
• cur++

2.然后从后向前复写

这里有个例外需要额外处理一下

以上这种情况在我们进行从后向前复写的时候会发生越界访问把这个位置给修改为0，在LeetCode上越界访问会直接报错，所以我们要单独处理一下这种情况

n-1位置直接修改为0，在让dest -= 2，cur--;

参考代码如下：

class Solution {
public:
    void duplicateZeros(vector<int>& arr) {
        int dest = -1;
        int cur = 0;
        //找到最后一个复写
        while(cur < arr.size())
        {
            if(arr[cur] == 0)
            {
                dest += 2;
            }
            else
            {
                dest++;
            }
            if(dest >= arr.size()-1)
            {
                break;
            }
            cur++;
        }
         //处理越界
        if(dest == arr.size())
        {
            arr[arr.size()-1] = 0;
            --cur;
            dest -= 2;
        }
        
        while(dest >= 0)
        {
            if(arr[cur] == 0)
            {
                arr[dest--] = 0;
                arr[dest--] = 0;
                cur--;
            }
            else
            {
                arr[dest--] = arr[cur--];
            }
            
        }
        
    }
};

3.快乐数

快乐数

题目描述：

题目分析：

题目意思大概就是这样。

思路：我们之前在数据结构中不是学了一个判断链表是否有环，这里就可以运用起来，使用快慢双指针。

1.定义快慢指针

2.快慢指针每次向后移动一步，快指针每次向后移动两步

3.判断相遇时候的值即可。

参考代码如下：

class Solution {
public:
    int bitSum(int n)
    {
        int sum = 0;
        while(n)
        {
            int t = n % 10;
            sum += t * t;
            n /= 10;

        }
        return sum;
    }
    bool isHappy(int n) {
        int slow = n,fast = bitSum(n);
        while(slow != fast)
        {
            slow = bitSum(slow);
            fast = bitSum(bitSum(fast));
        }
        return slow == 1;

    }
};

4.盛最多水的容器

盛最多水的容器

题目描述：

题目分析：如示例1：下标为1的它的高度是8和下标为8的它的高度为7这个容器的高度不能超过7，也就是取他们的最小值，那么从下标1到下标8的宽度为7，也就是下标为1到下标为8的距离，得出高为7宽为7相乘得出49那么最多容纳水量49，而我们要取这个容器里面的最大水量。

思路：

解法一：大部分人最容易想到的就是用两个for循环暴力枚举，让1和后面的数依次枚举，但是这样时间复杂度是O(N^2)效率太低。

解法二：

利用单调性，使用双指针来解决问题时间复杂度O(N)

我们使用双指针一个left一个right，选取这两个数的最小值也就是高度，然后让right减left得出宽度进行计算即可，把结果存储起来选出最大值也就是最大水量了，然后我们让小的那个数往前走，依次内推，这里我们知道如果一个数的宽度总是在减小那么这个水容量也会减小，而我们需要的是最大水容量。

参考代码：

class Solution {
public:
    int maxArea(vector<int>& height) 
    {
        int left = 0,right = height.size()-1,ret = 0;
        while(left < right)
        {
            int v = min(height[left],height[right]) * (right - left);
            ret = max(v,ret);
            if(height[left] < height[right]) ++left;
            else --right;
        }
        return ret;
    }
};

5. 有效三角形的个数

有效三角形的个数

题目描述：

思路：

解法一：暴力枚举，下面是一个伪代码，它的时间复杂度是O(N^3)，效率太低

解法二：我们先把数组排序一下然后使用双指针算法，我们让left+right的结果和最后一个也就是最大值进行比较如果大于说明right-left这个区间的值都能组成我们直接让right--，如果left-right的结果小于最大值说明right-left这个区间不能组成所以我们left++，比较完之后我们在让倒数第二个元素做为最大值对他们进行比较，以此内推。时间复杂度为O(N^2)

参考代码：

class Solution {
public:
    int triangleNumber(vector<int>& nums) {

        sort(nums.begin(),nums.end());
        int ret = 0,n = nums.size()-1;
        for(int i = n;i >= 2;i--)
        {
            int left = 0,right = i-1;
            while(left < right)
            {
                if(nums[left] + nums[right] > nums[i])
                {
                    ret += right -left;
                    --right;
                }
                else
                {
                    ++left;
                }
            }
        }
        return ret;
    }
};

6.查找总价格为目标的两个商品

查找总价格为目标的两个商品

题目描述：

解法一：如下是伪代码

解法二：本题解法使用双指针，我们让最左边的值和最右边的值进行相加然后和target进行比较那么比较的结果无法就是三种，第一种sum > t，第二种sum<t，第三张sum==t（sum就是左边和右边之和），如果大于t说明left到right都大于那么我们-right即可，如果小于t说明left到right都小于t所以++left即可，以此内推。

参考代码：

class Solution {
public:
    vector<int> twoSum(vector<int>& price, int target) {
        int n = price.size()-1;      
        int left = 0,right = n;
        vector<int>v;
        while(left < right)
        {
            int sum = price[left] + price[right];
            if(sum > target)
            {
                --right;
            }
            else if(sum < target)
            {
                ++left;
            }
            else{
               return {price[left],price[right]};
                
            }
        }
        return {-1,-1};
        
    }
};

7.三数之和

三数之和

题目描述：

题目分析：

我们看示例1可以看到三个数相加之和要等于0，题目中说不可以重复那是什么意思呢，如上我们可以看到-1 0 1和0 1 -1还有-1 1 0他们都等于0但是他们里面的元素是相同的只不过位置不同这样就重复了只需一种即可。

思路：

解法一：排序+暴力解法+利用set去重，时间复杂度 o(N^3),暴力解法其实就是一个一个去试三个for循环

解法二：我们依旧使用双指针，如下：

1. 排序
2. 固定一个数a(a<=0，因为已经排过序了如果a>0那么left+right只会更加大，因为left是从a后面开始的)
3. 在该数后面的区间内，利用“双指针算法”快速找到两个的和等于-a即可。

处理细节问题：

1.去重

• 找到一种结果之后left和right指针要跳过重复元素
• 当使用完一次双指针算法之后，i也需要跳过重复的元素
• 注意：避免越界

2.不漏

• 找到一种结果之后，不要“停”，缩小区间，继续寻找

 参考代码：

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int n = nums.size();
        vector<vector<int>> ret;
        for(int i = 0;i <n;)
        {
            int left = i+1,right = n-1,target = -nums[i];
            if(nums[i] > 0) break;
            while(left < right)
            {
                int sum = nums[left] + nums[right];
                if(sum > target) --right;
                else if(sum < target) ++left;
                else
                {
                    ret.push_back({nums[i],nums[left],nums[right]});
                    ++left,--right;
                    //去重left，right
                    while(left < right && nums[left] == nums[left -1]) ++left;
                    while(left < right && nums[right] == nums[right + 1]) --right;
                }
            }
            //去重i
            i++;
            while(i < n && nums[i] == nums[i-1]) ++i;

        }
        return ret;
    }
};

8.四数之和

四数之和

题目描述：

这个题和三数之和的题类似

解法一：排序+暴力枚举+利用set去重

解法二：排序+双指针

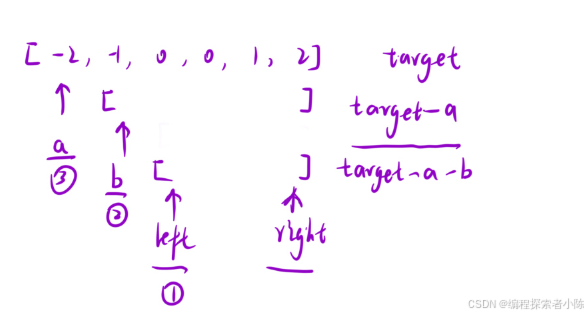
1. 依次固定一个数a；
2. 在a后面的区间内，利用“三数之和”找到三个数使这三个数等于target-a即可

补充一下上面说的三数之和：

1. 依次固定一个数b
2. 在b后面的区间内，利用“双指针”找到两个数使这两个的和等于target-a-b即可。

时间复杂度O(N^3) 

参考代码：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(),nums.end());
        vector<vector<int>>ret;
        int n = nums.size();
        for(int i = 0;i<n;)
        {
            for(int j = i+1;j<n;)
            {
                long long amin = (long long)target - nums[i] - nums[j];
                int left = j +1,right = n-1;
                while(left < right)
                {
                    int sum = nums[left] + nums[right];
                    if(left < right && sum > amin)--right;
                    else if(left < right && sum < amin) ++left;
                    else
                    {
                        ret.push_back({nums[i],nums[j],nums[left++],nums[right--]});
                        //去重left,right
                        while(left < right && nums[left] == nums[left-1]) ++ left;
                        while(left < right && nums[right] == nums[right+1]) -- right;
                    }
                }
                //去重j
                j++;
                while(j < n && nums[j] == nums[j-1]) ++ j;
            }
            //去重i
            i++;
            while(i < n && nums[i] == nums[i-1]) ++ i;
        }
        return ret;
    }
    
};

结束语：

掌握双指针算法对于解决复杂问题至关重要，刷题则是积累经验、提升能力的关键途径。通过不断练习，我们不仅能提升自己的解题速度和准确性，更能培养灵活运用各种算法的能力，为解决更为复杂的问题打下坚实基础。