Python：《寻找整数》

问题描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

有一个不超过 1017 的正整数 n，知道这个数除以 2 至 49 后的余数如下表所示，求这个正整数最小是多少。

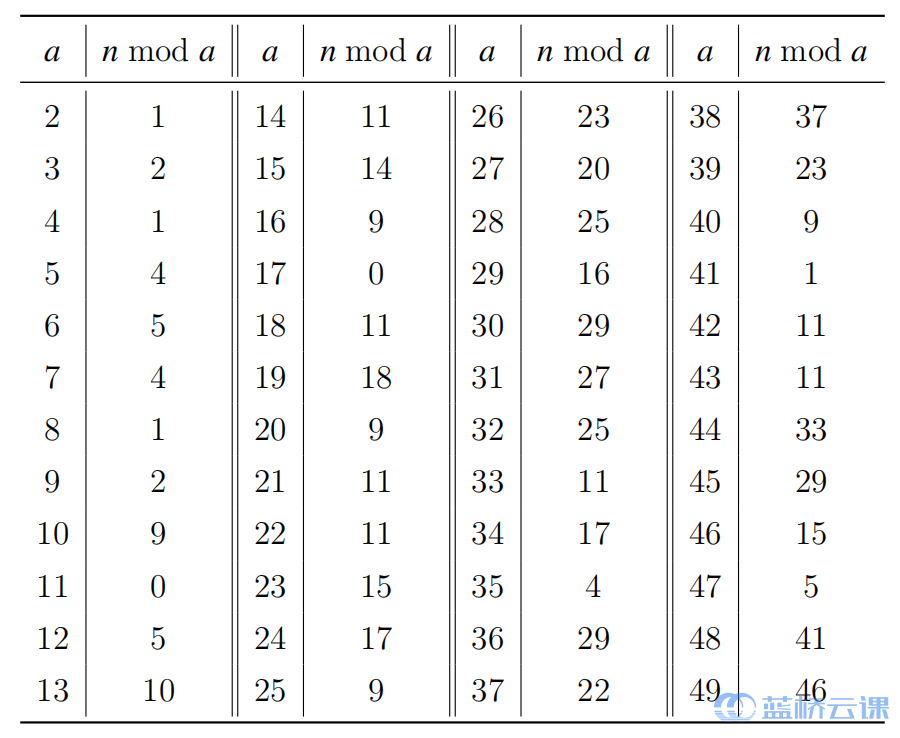
运行限制

• 最大运行时间：1s
• 最大运行内存: 512M 

思路： 

考虑第一个约束条件： n ，可以发现所有满足的数字均为奇数： 1,3,5,7,... ，此时满足条件的数字相差 2 ，这是由于模数为 2 。

考虑前两个约束条件： n ，可以发现所有满足的数字为： 5,11,17,... ，此时满足条件的数字相差 6 ，这是由于模数为 2,3 ，而 2,3 的最小公倍数为 6 。

考虑前三个约束条件： n ，可以发现所有满足的数字为： 5,17,29 ，此时满足条件的数字相差 12 ，这是由于模数为 2,3,4 ，而 (2,3,4)=12lcm(2,3,4)=12 。

上述发现为一元同余线性方程组的性质：

x≡a1​(mod m1​)x≡a2​(mod m2​)...x≡an​(mod mn​)

如果 x^ 为 x 的最小整数解，则通解为 x^+k⋅lcm(m1​,m2​,...mn​) 。

根据这个性质，我们可以暴力枚举求解上述结果，最开始初始数字 x=0 ，步长 step=1 ，对于第 i 个条件 (2≤i≤49) ：

• x 不断加上 step ，暴力找到满足第 i 个条件的新解 xi​
• 更新 step=lcm(step,i)
• 更新 x=xi​

这样不断扩大步长，可以保证始终满足前 i−1 个条件，暴力求解满足第 i 个条件的数字即可。

 参考代码：

from math import gcd  #导入最大公约数
def lcm(a,b):
  return a*b//gcd(a,b) #利用最大公约数求最小公倍数

a=[0,0,1,2,1,4,5,4,1,2,9,0,5,10,11,14,9,0,11,18,9,11,11,15,17,9,23,20,25,16,29,27,25,11,17,4,29,22,37,23,9,1,11,11,33,29,15,5,41,46]
stap=1
x=0
for i in range(2,50):
  while x%i!=a[i]:
    x+=stap
  stap=lcm(stap,i)
print(x)

Python math.gcd() 方法 

# 导入 math 包
import math

# 输出最大公约数
print (math.gcd(3, 6))
print (math.gcd(6, 12))
print (math.gcd(12, 36))
print (math.gcd(-12, -36))
print (math.gcd(5, 12))
print (math.gcd(10, 0))
print (math.gcd(0, 34))
print (math.gcd(0, 0))
输出结果：

3
6
12
12
1
10
34
0