08基于拉丁超立方法的风光场景生成与削减

需要代码可见博主资源：https://download.csdn.net/download/qq_50594161/87607550

下面有部分代码，但由于篇幅限制故上传至资源中，不要积分哦。

MATLAB代码：基于拉丁超立方法的风光场景生成与削减

参考文档《基于拉丁超立方法的风光场景生成与削减》

仿真平台：MATLAB

摘要：与蒙特卡洛法不同，拉丁超立方采样改进了采样策略能够做到较小采样规模中获得较高的采样精度，属于分层抽样技术，设定风光出力遵从正态分布normrnd，从而实现场景的大规模生成，并通过概率距离快速削减法完成了场景的削减，出图效果可以见下图哦！

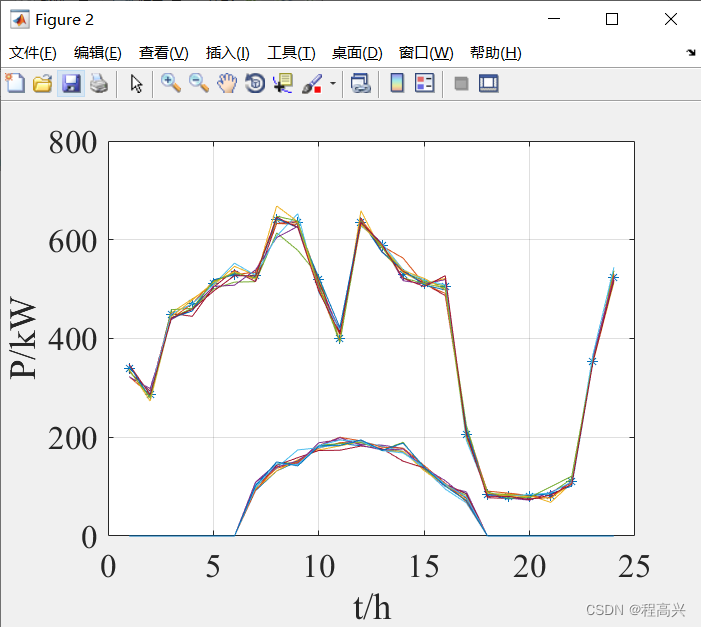
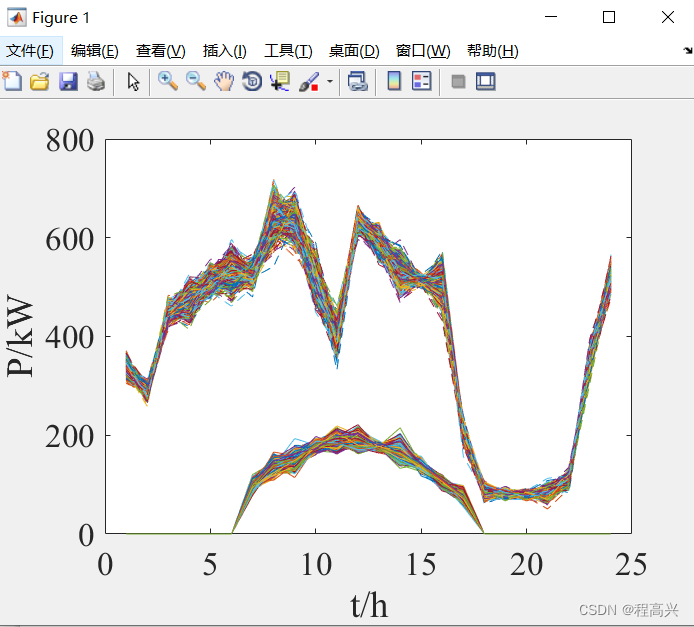
clc
clear all
%%
%场景法
%%% wf1 wf2 为平均值
wf1=[339,287,449,471,512,530,527,641,634,519,401,634,589,530,512,505,206,85,81,80,83,110,353,523];
wf2=[0,0,0,0,0,0,99,137,150,178,189,191,176,171,138,104,77,0,0,0,0,0,0,0];
m1=ones(24,1000);%风生成
m2=ones(24,1000);%光生成
m=ones(24,1000);%可再生生成
%%
%生成1000个场景
%%
%拉丁差立方抽样方法
%%%拉丁超级方抽样=====属于分层抽样技术（从多元参数分布中近似随机抽样的方法）------分层抽样：将抽样区间(本程序为正态分布区间)
          %按某种特性或某种规划分为不同的层，然后从不同的层中独立、随机（打乱排序，无规律抽取）
          %地抽取样本（如取10个苹果样本，按照特性把苹果树分为5类，每类随机取2个），从而保证样本的结构与总体的结构比较相近，提高估计的精度。
          
%拉丁超立方相较蒙卡，改进了采样策略能够做到较小采样规模中获得较高的采样精度。

%%lhsnorm(mu,sigma,n); mu平均值(数量a)； 求解公式：u=(1/N)*(sum(样本))；N为样本数目
                 %     sigma协方差矩阵(数量a*a); 求解公式: =((1/N)^3)*(sum(样本i-u)^2);   i=1至N
                 %     n抽样次数
% 表示方式1
c=1;%c 表示基础数据的数量
u1=lhsdesign(1,24);
u2=lhsdesign(1,24);