GO--堆（have TODO）

堆

堆（Heap）是一种特殊的数据结构。它是一棵完全二叉树（完全二叉树是指除了最后一层外，每一层上的节点数都是满的，并且最后一层的节点都集中在左边），结放在数组（切片）中，通常分为最大堆（Max Heap）和最小堆（Min Heap）两种类型。

• 最大堆：在最大堆中，对于每个非叶子节点，它的值都大于或等于其左右子节点的值。也就是说，根节点的值是整个堆中的最大值。例如，对于节点i，如果它有左子节点2i + 1和右子节点2i+2（这里假设节点编号从 0 开始），那么heap[i]>=heap[2i + 1]且heap[i]>=heap[2i+2]。
• 最小堆：与最大堆相反，在最小堆中，对于每个非叶子节点，它的值都小于或等于其左右子节点的值。根节点的值是整个堆中的最小值。即对于节点i，heap[i]<=heap[2i + 1]且heap[i]<=heap[2i+2]。

堆的实现

1、使用container/heap包

heap源码中定义了一个Interface 的接口，此接口一共包含五个方法，我们定义一个实现此接口的类就实现了一个二叉堆

package main

import (
	"container/heap"
	"fmt"
)

type MaxHeap []int

func (m MaxHeap) Len() int {
	return len(m)
}

func (m MaxHeap) Less(i, j int) bool {
	//建立大根堆，使用>
	return m[i] > m[j]
}

func (m *MaxHeap) Swap(i, j int) {
	(*m)[i], (*m)[j] = (*m)[j], (*m)[i]
}

func (m *MaxHeap) Push(x any) {
	*m = append(*m, x.(int))
}

func (m *MaxHeap) Pop() any {
	//拿到堆顶元素
	res := (*m)[len(*m)-1]
	//删除堆顶元素
	*m = (*m)[:len(*m)-1]
	return res
}

func main() {
	h := make(MaxHeap, 0)
    //结构体实现了接口中的全部方法后，结构体也就是这个接口类型了，因此我们可以传入h
	heap.Init(&h)

	heap.Push(&h, 2)
	heap.Push(&h, 1)
	heap.Push(&h, 3)

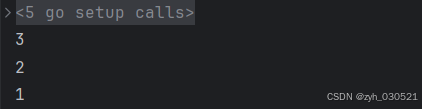
	fmt.Println(heap.Pop(&h))
	fmt.Println(heap.Pop(&h))
	fmt.Println(heap.Pop(&h))

}

下面我们一起去看看源码：

// Copyright 2009 The Go Authors. All rights reserved.
// Use of this source code is governed by a BSD-style
// license that can be found in the LICENSE file.

// Package heap provides heap operations for any type that implements
// heap.Interface. A heap is a tree with the property that each node is the
// minimum-valued node in its subtree.
//
// The minimum element in the tree is the root, at index 0.
//
// A heap is a common way to implement a priority queue. To build a priority
// queue, implement the Heap interface with the (negative) priority as the
// ordering for the Less method, so Push adds items while Pop removes the
// highest-priority item from the queue. The Examples include such an
// implementation; the file example_pq_test.go has the complete source.
package heap

import "sort"

// The Interface type describes the requirements
// for a type using the routines in this package.
// Any type that implements it may be used as a
// min-heap with the following invariants (established after
// [Init] has been called or if the data is empty or sorted):
//
//	!h.Less(j, i) for 0 <= i < h.Len() and 2*i+1 <= j <= 2*i+2 and j < h.Len()
//
// Note that [Push] and [Pop] in this interface are for package heap's
// implementation to call. To add and remove things from the heap,
// use [heap.Push] and [heap.Pop].


堆的接口，定义实现该接口内部的全部方法后，我们定义的类就实现了堆
下面是sort.Interface的实现，内部有三个方法，分别是Len（）、Less（）、Swap（）
通过Less（）方法，以此确定建立的是大根堆，还是小根堆

// An implementation of Interface can be sorted by the routines in this package.
// The methods refer to elements of the underlying collection by integer index.
type Interface interface {
	// Len is the number of elements in the collection.
	Len() int

	// Less reports whether the element with index i
	// must sort before the element with index j.
	//
	// If both Less(i, j) and Less(j, i) are false,
	// then the elements at index i and j are considered equal.
	// Sort may place equal elements in any order in the final result,
	// while Stable preserves the original input order of equal elements.
	//
	// Less must describe a transitive ordering:
	//  - if both Less(i, j) and Less(j, k) are true, then Less(i, k) must be true as well.
	//  - if both Less(i, j) and Less(j, k) are false, then Less(i, k) must be false as well.
	//
	// Note that floating-point comparison (the < operator on float32 or float64 values)
	// is not a transitive ordering when not-a-number (NaN) values are involved.
	// See Float64Slice.Less for a correct implementation for floating-point values.
	Less(i, j int) bool

	// Swap swaps the elements with indexes i and j.
	Swap(i, j int)
}


^
|
|
| 
重点

type Interface interface {
	sort.Interface
	Push(x any) // add x as element Len()
	Pop() any   // remove and return element Len() - 1.
}

|
|
|
——


init方法，将实现接口的类init进行建堆

// Init establishes the heap invariants required by the other routines in this package.
// Init is idempotent with respect to the heap invariants
// and may be called whenever the heap invariants may have been invalidated.
// The complexity is O(n) where n = h.Len().
func Init(h Interface) {
	// heapify
	n := h.Len()
	for i := n/2 - 1; i >= 0; i-- {
		down(h, i, n)
	}
}


Push插入元素

// Push pushes the element x onto the heap.
// The complexity is O(log n) where n = h.Len().
func Push(h Interface, x any) {
	h.Push(x)
	up(h, h.Len()-1)
}

Pop弹出元素

// Pop removes and returns the minimum element (according to Less) from the heap.
// The complexity is O(log n) where n = h.Len().
// Pop is equivalent to [Remove](h, 0).
func Pop(h Interface) any {
	n := h.Len() - 1
	h.Swap(0, n)
	down(h, 0, n)
	return h.Pop()
}


Remove移除元素

// Remove removes and returns the element at index i from the heap.
// The complexity is O(log n) where n = h.Len().
func Remove(h Interface, i int) any {
	n := h.Len() - 1
	if n != i {
		h.Swap(i, n)
		if !down(h, i, n) {
			up(h, i)
		}
	}
	return h.Pop()
}


Fix重新调整堆

// Fix re-establishes the heap ordering after the element at index i has changed its value.
// Changing the value of the element at index i and then calling Fix is equivalent to,
// but less expensive than, calling [Remove](h, i) followed by a Push of the new value.
// The complexity is O(log n) where n = h.Len().
func Fix(h Interface, i int) {
	if !down(h, i, h.Len()) {
		up(h, i)
	}
}


堆调整的两个重要方法，up和down，具体我没看，我们可以自己写出更简单更好理解的heapInsert和heapify

func up(h Interface, j int) {
	for {
		i := (j - 1) / 2 // parent
		if i == j || !h.Less(j, i) {
			break
		}
		h.Swap(i, j)
		j = i
	}
}

func down(h Interface, i0, n int) bool {
	i := i0
	for {
		j1 := 2*i + 1
		if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
			break
		}
		j := j1 // left child
		if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
			j = j2 // = 2*i + 2  // right child
		}
		if !h.Less(j, i) {
			break
		}
		h.Swap(i, j)
		i = j
	}
	return i > i0
}

2、自己实现堆

自己实现堆，最重要的就是heapInsert和heapify方法，通过这两个方法，以此保证正确实现堆结构。

heapInsert方法：新来的一个元素，新来的元素若大于他的父节点元素，则上升，确定其应该在堆中的正确位置，实现大根堆

for循环虽然只有一个判断，却包含了另一层判断，当index到达0位置后，循环也会停止

func heapInsert(arr []int, index int) {
	for arr[index] > arr[(index-1)/2] {
		arr[index], arr[(index-1)/2] = arr[(index-1)/2], arr[index]
		index = (index - 1) / 2
	}
}

heapify方法，节点位置为最大值，实现大根堆

func heapify(arr []int, index int, heapsize int) {
	//左孩子的位置
	left := index*2 + 1
	for left < heapsize {
		//largest的含义为：节点和子节点中的最大值
		largest := left 	//一开始放在左孩子上
		//如果存在右孩子，并且右孩子的值比左孩子大，以此选出左右孩子中的较大节点
		if left+1 < heapsize && arr[left] < arr[left+1] {
			//在largest放在右孩子的位置
			largest = left + 1
		}
		//判断largest和index节点位置谁大
		if arr[index] > arr[largest] {
			//若节点大于largest，则largest来到index位置
			largest = index
		}
		//index位置为最大，则退出循环，不需要向下进行
		if largest == index {
			break
		}
		//交换节点位置
		arr[largest], arr[index] = arr[index], arr[largest]
		//index来到largest位置，继续下次循环
		index = largest
		//left继续来到左孩子的位置
		left = index * 2 + 1
	}
}

建堆

// 建堆
func buildHeap(arr []int) {
	//从上至下建堆
	//for i := 0; i < len(arr); i++ {
	//	heapInsert(arr, i)
	//}

	//从下至上建堆
	for i := len(arr) - 1; i >= 0; i-- {
		heapify(arr, i, len(arr))
	}

}

堆排序

能够自己实现堆之后，实现堆排序就十分简单了。

若我们实现了大根堆，那么每次堆顶元素就是最大值，那么只需要堆顶与最后一个元素进行交换，交换后，堆的大小减1，然后在将交换后位于第一位的元素使用heapify让其下降，这样循环进行，最后堆的大小减到0，那么就实现了排序。

func heapSort(arr []int) {
	heapSize := len(arr)
	heapSize--
	arr[0], arr[heapSize] = arr[heapSize], arr[0]
	for heapSize > 0 {
		heapify(arr, 0, heapSize)
		heapSize--
		arr[0], arr[heapSize] = arr[heapSize], arr[0]
	}
}

Leetcode堆相关题目

（累了，下次再写）

1、215. 数组中的第K个最大元素 - 力扣（LeetCode）

求数组中第K大的元素，有很简单的方法，将数组进行排序，返回第k个数，即为第k大的数。

题目要求时间复杂度为O(N)，可以使用桶排序，这道题目给了数据范围，确实可以用。

题解里还有改进的快速排序，也能达到O(N)的时间复杂度。

但我们主要还是使用堆来完成。

//题解标准答案
func findKthLargest(nums []int, k int) int {
	//建立大根堆
	buildHeap(nums)
	heapSize := len(nums)
	for i := len(nums) - 1; i >= len(nums)-k+1; i-- {
		nums[0], nums[i] = nums[i], nums[0]
		heapSize--
		heapify(nums, 0, heapSize)
	}

	return nums[0]
}

//我觉得不好理解，就自己写了i从0——K，但是需要加判断，要不会出现nums[-1]的报错
func findKthLargest(nums []int, K int) int {
	buildHeap(nums)
	heapSize := len(nums)
	nums[0], nums[heapSize-1] = nums[heapSize-1], nums[0]
	for i:= 0; i < K; i++ {
		heapSize--
		heapify(nums,0,heapSize)
		if heapSize-1 >= 0{
			nums[0], nums[heapSize-1] = nums[heapSize-1], nums[0]
		} else {
			return nums[heapSize]
		}
	}
	return nums[heapSize]
}


func heapify(arr []int, index int, heapsize int) {
	//左孩子的位置
	left := index*2 + 1
	for left < heapsize {
		//largest的含义为：节点和子节点中的最大值
		largest := left //一开始放在左孩子上
		//如果存在右孩子，并且右孩子的值比左孩子大，以此选出左右孩子中的较大节点
		if left+1 < heapsize && arr[left] < arr[left+1] {
			//在largest放在右孩子的位置
			largest = left + 1
		}
		//判断largest和index节点位置谁大
		if arr[index] > arr[largest] {
			//若节点大于largest，则largest来到index位置
			largest = index
		}
		//index位置为最大，则退出循环，不需要向下进行
		if largest == index {
			break
		}
		//交换节点位置
		arr[largest], arr[index] = arr[index], arr[largest]
		//index来到largest位置，继续下次循环
		index = largest
		//left继续来到左孩子的位置
		left = index*2 + 1
	}
}


func buildHeap(arr []int) {
	//从上至下建堆
	//for i := 0; i < len(arr); i++ {
	//	heapInsert(arr, i)
	//}

	//从下至上建堆
	for i := len(arr) - 1; i >= 0; i-- {
		heapify(arr, i, len(arr))
	}

}

2、502. IPO - 力扣（LeetCode）

3、373. 查找和最小的 K 对数字 - 力扣（LeetCode）

TODO

4、295. 数据流的中位数 - 力扣（LeetCode）

TODO