完全二叉树的4种遍历方式
一张二叉树的图
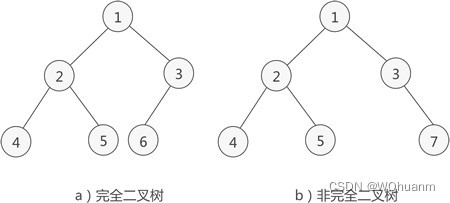
1,二叉树的特点
- 每个点p的左儿子是p*2,右儿子是p*2+1,可以分别表示为p<<1与p<<1|1
- 节点的序号是从左到右,从上到下增加的
- 每个点至多2个儿子(屁话(bushi))
2,先序遍历(根左右)
就是每次到子树的根节点,先存入这个节点,然后优先访问左儿子,左儿子访问到回来,再访问右儿子(不是亲生的(que ren))
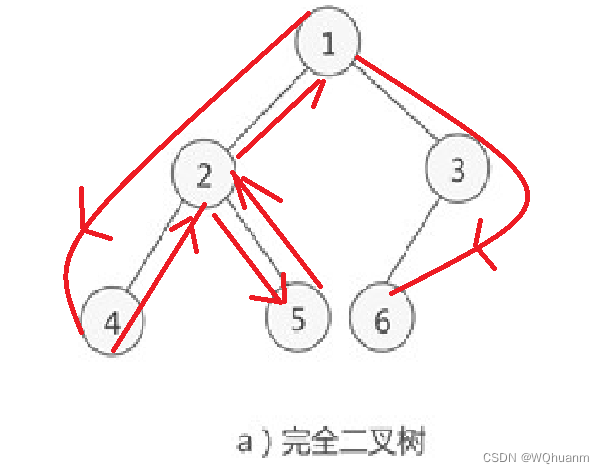
顺序1->2->4->5(正在回家的路上)->3->6
int t[N];//t表示树上节点
int cnt;
void build(int p)
{
cout<<t[p];//每次存储根节点后进入左儿子
build(p<<1);
build(p<<1|1);//左儿子出来后再进入右儿子
}3,中序遍历(左根右)
每次到子树的根节点,先进入左儿子,回来后在访问根,最后再访问右儿子
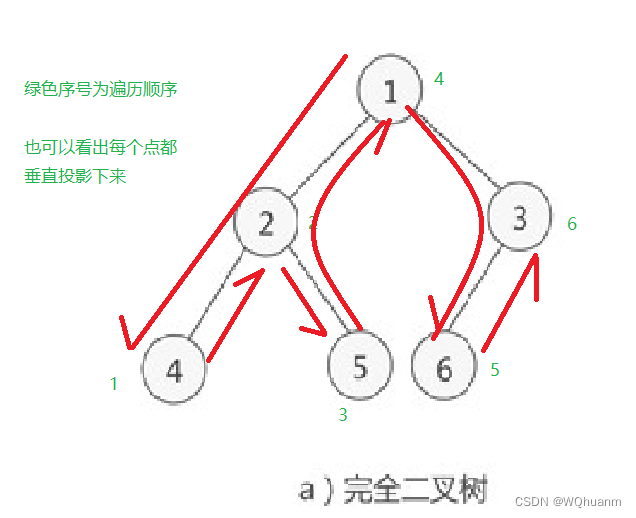
顺序4->2->5->1->6->3
int t[N];//t表示树上节点
int cnt;
void build(int p)
{
build(p<<1);//每次x先进入左儿子,出来后再存储根节点
cout<<t[p];
build(p<<1|1);//根节点存储后后再进入右儿子
}4,后序遍历(左右根)
依次访问左右儿子,再回来访问根节点
顺序是4->5->2->3->6->1
int t[N];//t表示树上节点
int cnt;
void build(int p)
{
build(p<<1);//每次x先进入左儿子
build(p<<1|1);//再进入右儿子
cout<<t[p];//最后存储根节点
}5,层序遍历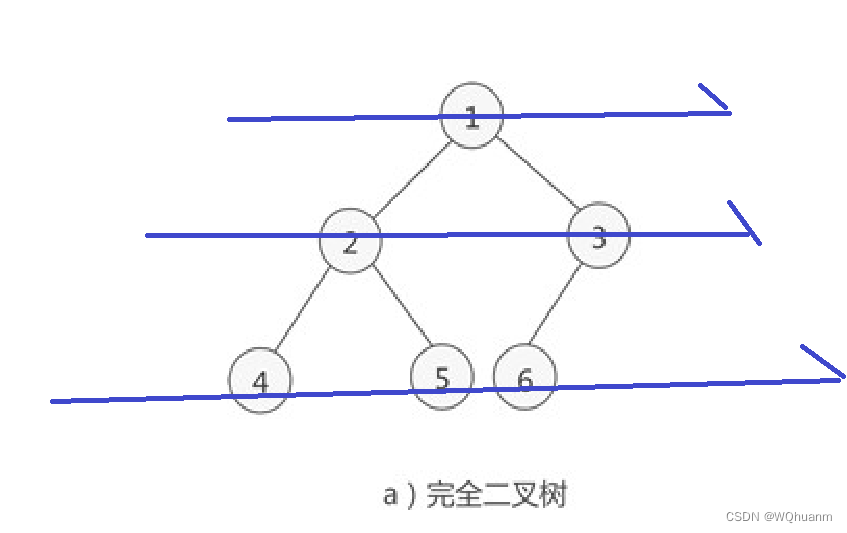
就是一层一层访问,这次不再是遍历了,我们观察序号,其实
t[1]~t[n]就是点1~n的层序遍历
int t[N];//t表示树上节点
int cnt;
for (int i=1; i<=n; ++i)cout<<t[i]<<endl;
