109.【C语言】数据结构之求二叉树的高度

目录

1.知识回顾：高度（也称深度）

2.分析 

设计代码框架

 返回左右子树高度较大的那个的写法一:if语句

 返回左右子树高度较大的那个的写法二:三目操作符

3.代码 

4.反思

问题

出问题的代码 

改进后的代码

执行结果

1.知识回顾：高度（也称深度）

参见100.【C语言】数据结构之二叉树的基本知识

以这个二叉树为例,其高度为4

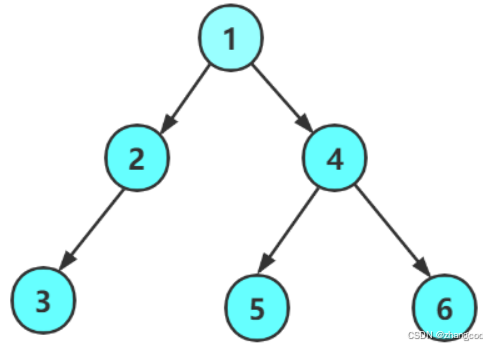
2.分析 

“分而治之”的思想+递归:

将任务交给多个“下属”去做

递推:

整个树的高度==根节点的高度+左右子树高度中较大的高度

左子树的高度==根节点的高度+其左右子树高度中较大的高度

右子树的高度==根节点的高度+其左右子树高度中较大的高度

......

回归:当节点为NULL时(即遇到空树),回归

核心思想:左树和右树高度较大的那个将高度的结果+1(+1代表左树或右树的根节点的高度)报告给根

设计代码框架

节点为NULL时(即遇到空树)的情况优先判断,由于TreeHeight函数的返回值为int,因此return 0;

int TreeHeight(BTNode* root)
{
    //节点为NULL,优先处理
    if (root==NULL)
        return 0;

    //如果不为NULL
    {
        //返回左右子树高度较大的那个
    }
}

 返回左右子树高度较大的那个的写法一:if语句

if (TreeHeight(root->left) > TreeHeight(root->right))
    TreeHeight(root->left) + 1;
else
    TreeHeight(root->right) + 1;

 返回左右子树高度较大的那个的写法二:三目操作符

return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;

3.代码 

由上述分析可知:

int TreeHeight(BTNode* root)
{
    if (root==NULL)
        return 0;

    return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}

4.反思

问题

当二叉树的节点节点过多结构较复杂时,会发现代码的执行效率低下,运行时间过长,是什么原因导致的?

答:运行时间过长肯定是因为递归调用的次数过多

出问题的代码 

return TreeHeight(root->left) > TreeHeight(root->right) ? TreeHeight(root->left) + 1 : TreeHeight(root->right) + 1;
}

先进行TreeHeight(root->left) > TreeHeight(root->right),之后执行TreeHeight(root->left) + 1或TreeHeight(root->right) + 1

显然TreeHeight函数被反复调用,越往下的节点,TreeHeight对其调用的次数越多,问题出在:比较时高度时并没有保存函数的返回值,时间复杂度为

改进后的代码

只需要在比较时保存TreeHeight函数的返回值即可

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int leftheight = TreeHeight(root->left);
	int rightheight = TreeHeight(root->right);
	return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}

Tree.h写入

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

BTNode* BuyNode(BTDataType x);
BTNode* CreateTree();
int TreeHeight(BTNode* root);

Tree.c写入

#include "Tree.h"
BTNode* BuyNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		perror("malloc");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}

BTNode* CreateTree()
{
	//写入各个节点的数据域
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	//	BTNode* node7 = BuyNode(6);
		//设置left和right指针
	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	//node3->right = node7;
	//返回根节点的指针
	return node1;
}

int TreeHeight(BTNode* root)
{
	if (root == NULL)
		return 0;
	int leftheight = TreeHeight(root->left);
	int rightheight = TreeHeight(root->right);
	return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
}

main.c写入

#include "Tree.h"
int main()
{
	BTNode* root=CreateTree();
	printf("TreeHight=%d", TreeHeight(root));
}

执行结果