【电路理论四】正弦电流电路
正弦电流
正弦量是随时间按正弦规律变动的电路变量。
随时间按正弦规律变动的电流称为正弦电流。
正弦电流的瞬时值表达式:
称为正弦电流的三要素。
分别为振幅/幅值,角频率,初相。
幅值为正弦电流的最大值,恒为正。
为正弦电流的相位,在t=0时刻的相位
为初相,一般初相的绝对值小于180度
角频率为单位时间内相位变动的角度。单位rad/s
有效值是瞬时值的平方在一个周期内的平均值再开方,也称方均根值(RMS)
正弦电流的有效值
其中
则代入得:
则可得正弦电流瞬时值另一种表达式:
同频率正弦量的相位差为初相之差
对于u和i两个同频率正弦量
相位差:
若相位差为0,则为同相。若相差为90°,则称他们相位正交。
相位差大于零,则称u超前i。
反之则为u滞后i
初相为零的正弦量称为参考正弦量。
正弦量的相量表示法
复数的运算略
可以自己参照数学资料

相量表示这一块是重点!

注意:
相量是复值常量,而正弦量是时间的余弦函数,相量只是代表正弦量,而不等于正弦量。
几何意义:正弦量的瞬时值等于其对应的旋转相量在实轴上的投影。


基尔霍夫定律的相量表示
KCL的表示如下

在集中参数正弦电流电路中,流出(流入)任一节点的电流相量的代数和等于零。
KVL同理
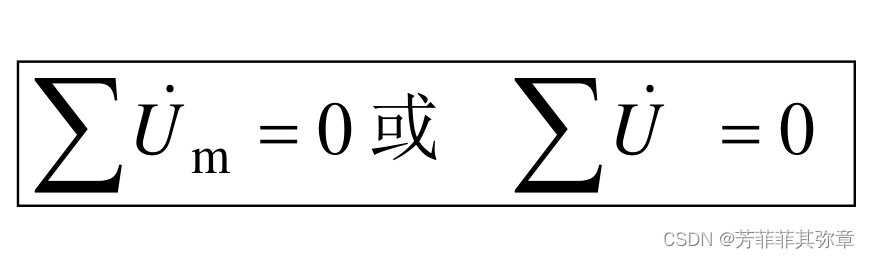
在集中参数正弦电流电路中,沿任一回路各支路电压相量的代数和等于零。
一个例子

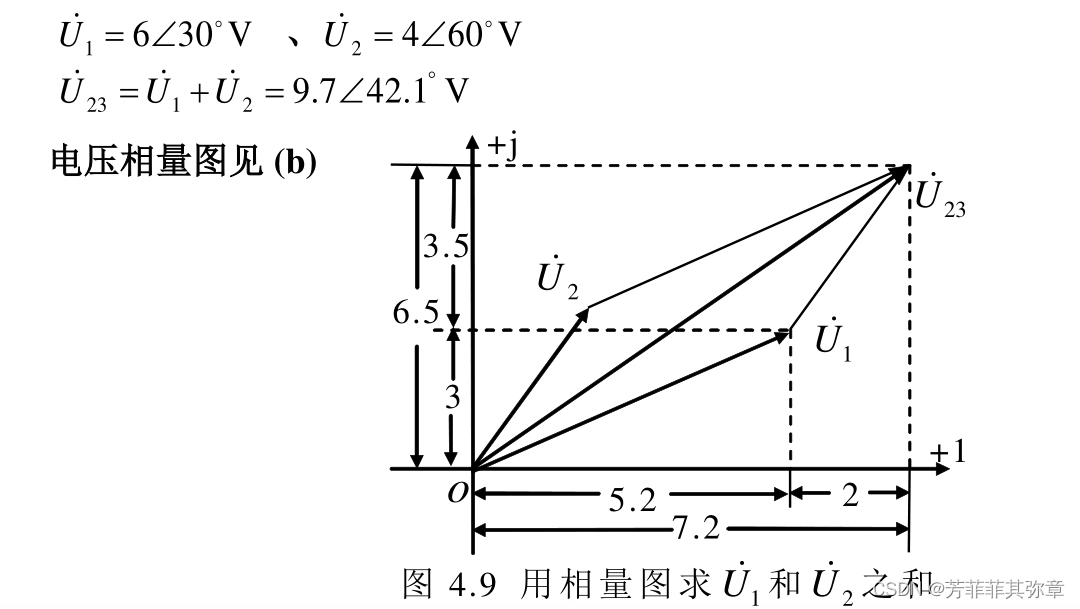
RLC元件上电压与电流的相量关系
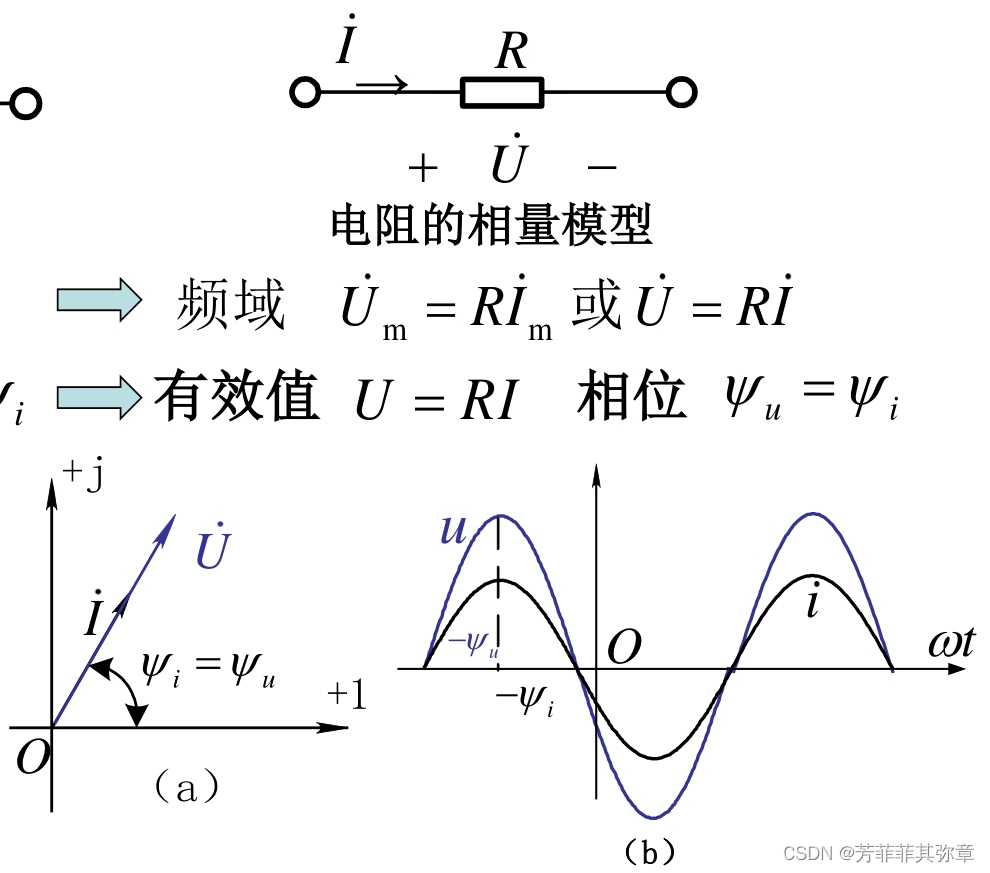
电阻R上电压电流有效值(或振幅)之比等于电阻;电压与电流同相位。
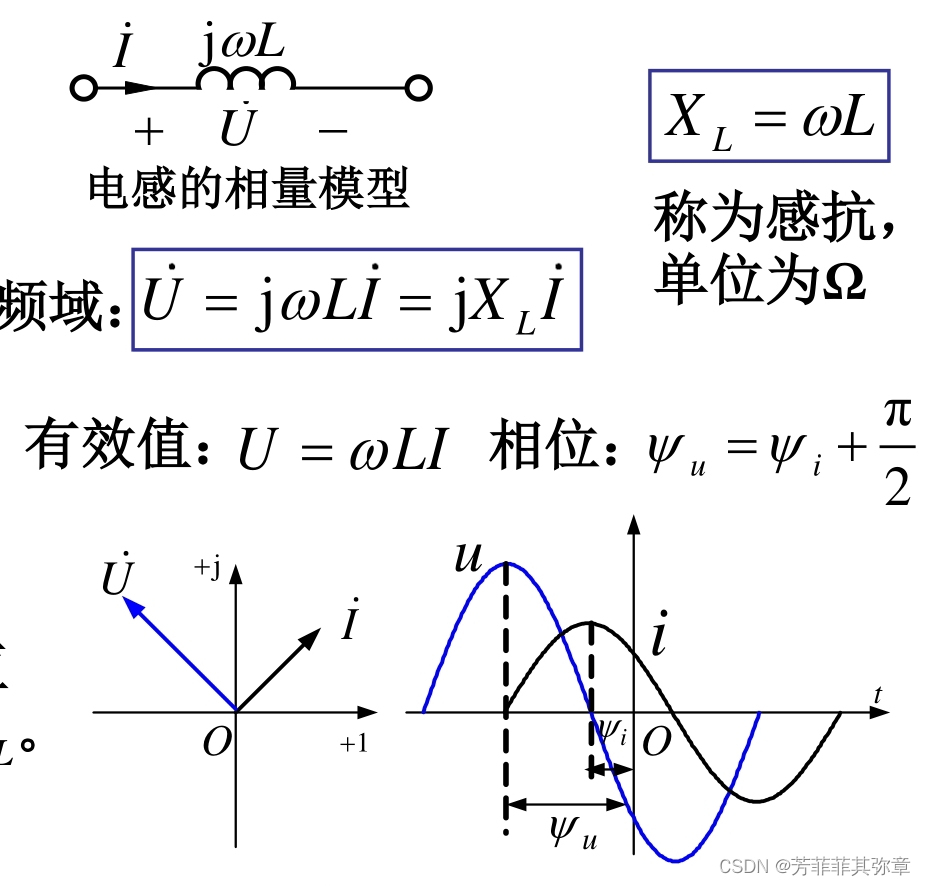
电感L上电压比电流越前90°;电压、电流有效值(或幅值)之比等于感抗XL。
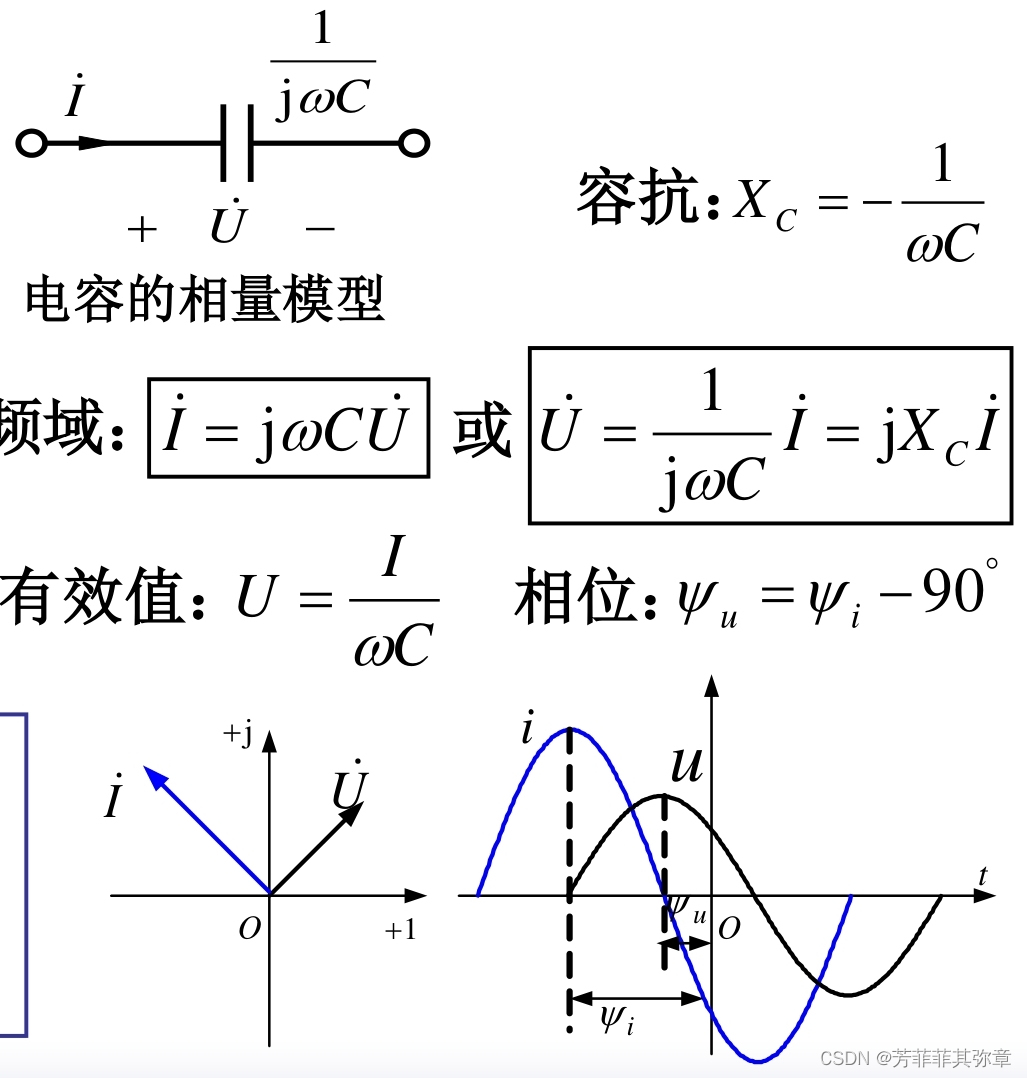
电容C上电压、电流有效值(或振幅)之比等于容抗的绝对值;电压比电流滞后90°。
导纳和阻抗
线性无独立源一端口在正弦激励下处于稳态时,端口电压相量与电流相量的比值定义为该一端口的阻抗Z
 对于RLC电路,阻抗Z为:
对于RLC电路,阻抗Z为:

可从中知晓感性,容性,阻性的区别
导纳就是反过来,具体内容略。
正弦电流电路的相量分析法
直流推广为交流,所有的直流定理由于相量分析,都可以与交流情形一一对应。
一个例子:

正弦电流电路的功率
一端口网络的端口电压、电流分别为
,
设相位差
则p=ui,化简可得如下形式:

p有时为正,有时为负;
p>0,电路吸收功率;p<0,电路发出功率。
还有第二种分解方法:
后者为时间的正弦函数,反映一端口网络与外电路交换能量,它在一个周期的平均值为零

无功功率:
一端口网络和外部电路能量交换的最大速率定义为无功功率。单位:var(乏)
在RLC串联电路中
电阻只提供有功功率,电容、电感只提供无功功率。
视在功率(表观功率)
单位伏安(VA),表示电气设备容量。
显然有:
提高功率因数的意义:
(1)通过减少线路电流来减小线路损耗;
(2)提高发电设备利用率。
解决办法:对于感性负载并联电容,提高功率因数
一个例子:

最大功率传输原理

最大功率传输定理:负载阻抗等于电源内阻抗的共轭复数时(称为共轭匹配),负载获得最大功率,此时最大功率为:
