当前位置：首页 > article >正文

[DFS]

article 2025/1/15 16:50:22

自写组合算法

dfs时，选或不选第k个数，就实现了各种组合。

打印二进制数

vis=[0]*10
def dfs(k,s):
    if k==3:
        print(s)
    else:
        vis[k]=0#选第k个数
        dfs(k+1,s+'0')
        vis[k]=1#不选第k个数
        dfs(k+1,s+'1')
dfs(0,'')

树上DFS

树的重心

树的重心u:

以树上任意一个结点为根计算它的子树的结点数,如果结点u的最大的子树的结点数最少，那么u就是树的重心。即删除点u后得到两棵或更多棵互不连通的子树,其中最大子树的结点数最小。u是树上最平衡的点。

那么如何计算结点的数量呢，

教父

时间限制： 2000MS

内存限制： 65536K

描述

去年芝加哥充满了黑帮斗殴和奇怪的谋杀案。警察局长真的厌倦了所有这些罪行，并决定逮捕黑手党领导人。

不幸的是，芝加哥黑手党的结构相当复杂。已知有n个人与黑手党有关。警方追踪他们的活动有一段时间了，知道他们中的一些人正在互相交流。根据收集到的数据，警察局长建议可以将黑手党等级制度表示为一棵树。黑手党的头目教父是树的根，如果用树中的一个节点表示某个人，则其直属下属就是该节点的子节点。为了阴谋，歹徒只与他们的直接下属和他们的直接主人联系。

不幸的是，虽然警察知道歹徒的通讯方式，但他们不知道任何一对通讯人员中谁是高手。因此他们只有一棵无向的通信树，并且不知道教父是谁。

基于教父希望对黑手党有最大可能的控制的想法，警察局长提出了一个建议，教父是这样一个人，从通信树中删除它后，最大的剩余连接组件的大小尽可能小尽可能。帮助警察找到所有可能的教父，他们会逮捕他们。

输入

输入文件的第一行包含n — 被怀疑属于黑手党的人数（2 ≤ n ≤ 50 000）。让它们从 1 到n编号。

接下来的n -1 行每行包含两个整数。一对a i , b i表示歹徒a i与歹徒b i进行了通信。保证黑帮的通讯形成一棵树。

输出

打印所有被怀疑是教父的人的人数。数字必须按递增顺序打印，并以空格分隔。

样本输入

示例输出

2 3

import sys
sys.setrecursionlimit(300000)
def dfs(u,fa):
    global maxn
    global num
    tmp=0
    d[u]=1
    for er in edges[u]:#遍历u的子节点
        if er==fa:#不递归父亲
            continue
        dfs(er,u)#递归子节点，计算er这个子树的节点数量
        d[u]+=d[er]#计算以u为根的节点数量
        tmp=max(tmp,d[er])#记录u的最大子树的节点数量
    tmp=max(tmp,n-d[u])#与u父亲相连的另一半节点数量
    #以上计算出了u的最大连通块
    #下面计算疑似教父，如果每一个节点的最大连通块比其他节点的都小，它疑似教父
    if tmp<maxn:#一个疑似教父
        maxn=tmp#更新‘最小的’最大连通块
        num=1
        ans[num]=u#把教父记录在第一个位置
    elif tmp==maxn:
        num+=1
        ans[num]=u#如果疑似教父有多个，记录在后面
maxn=int(1e9)
n=int(input())
edges=[[] for i in range(n+1)]
d=[0]*(n+1)
ans=[0]*(n+1)
num=0
for i in range(n-1):
    a,b=map(int,input().split())
    edges[a].append(b)
    edges[b].append(a)
dfs(1,0)
s=sorted(ans[1:num+1])#对教父排序
for i in range(num):
    print(s[i],end=' ')#按顺序打印所有教父

求树的最长直径（非负权边）

进行两次DFS:

从点a开始找最长的边，其终点为b，再从点b开始找到最长的边，其终点为c，则从b到c就是最长的边，

贪心证明：将树当作绳子，将绳子拉到最长，其上面的节点会下垂，上面任意的节点所能到达的最长边的终点必定是两端点其中的一个，负责绳子一开始就不是拉着最长的状态。

import sys
sys.setrecursionlimit(300000)
def dfs(u,fa,d):#用dfs计算从u到每个子节点的距离
    dist[u]=d
    for er,w in edges[u]:
        if er!=fa:#关键，不回头搜素父节点
            dfs(er,u,d+w)
n=int(input())
edges=[[] for i in range(n+1)]
dist=[0]*(n+1)#记录距离
for i in range(n-1):
    a,b,w=map(int,input().split())
    edges[a].append((b,w))
    edges[b].append((a,w))
dfs(1,-1,0)
s=1
for i in range(1,n+1):#找到最远的节点s，s是直径的一个端点
    if dist[i]>dist[s]:
        s=i
dfs(s,-1,0)#从s出发，计算以s为起点，到树上每个节点的距离
t=1
for i in range(1,n+1):#找到直径的另一个端点t
    if dist[i]>dist[t]:
        t=i
print(dist[t])#打印树的直径长度

DFS拓扑排序

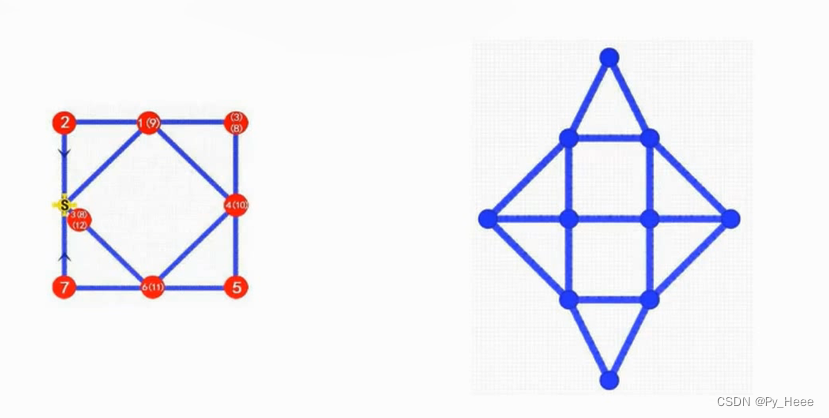
欧拉路与DFS

欧拉路:从图中某个点出发,遍历整个图,图中每条边通过且只通过一次。

图中所有的点连接的边是偶数倍，或者有且仅有起点和终点是奇数边，其他点均为偶数边。

欧拉回路:起点和终点相同的欧拉路。

图中所有的点连接的边是偶数倍

欧拉路问题:是否存在欧拉路、打印出欧拉路。