《自动驾驶与机器人中的SLAM技术》ch8:基于 IESKF 的紧耦合 LIO 系统
目录
基于 IESKF 的紧耦合 LIO 系统
1 IESKF 的状态变量和运动过程
1.1 对名义状态变量的预测
1.2 对误差状态变量的预测及对协方差矩阵的递推
2 观测方程中的迭代过程
3 高维观测中的等效处理
4 NDT 和 卡尔曼滤波的联系
5 紧耦合 LIO 系统的主要流程
5.1 IMU 静止初始化
5.2 ESKF 之 运动过程——使用 IMU 预测
5.3 使用 IMU 预测位姿进行运动补偿
5.4 松耦合系统的配准部分
参考
紧耦合系统,就是把点云的残差方程直接作为观测方程,写入观测模型中。这种做法相当于在滤波器或者优化算法内置了一个 ICP 或 NDT。因为 ICP 和 NDT 需要迭代来更新它们的最近邻,所以相应的滤波器也应该使用可以迭代的版本,ESKF 对应的可迭代版本的滤波器即为 IESKF。
紧耦合和松耦合的联系:
| 紧耦合LIO | 松耦合 LIO | |
| 预测 | 使用IMU读数预测得到先验位姿 | 同 |
| 观测 | 使用滤波器预测得到的先验位姿(首次)和更新后位姿(后续迭代)计算点云残差 | 使用点云配准部分迭代优化得到的位姿作为观测值,观测过程本身不迭代 |
| 更新 | 多次迭代,直到更新量dx满足要求 每次迭代都会以上一次更新的位姿来重新计算点云残差 | 一次更新 |

基于 IESKF 的紧耦合 LIO 系统
基于 IESKF 的紧耦合 LIO 系统的流程图如下所示:

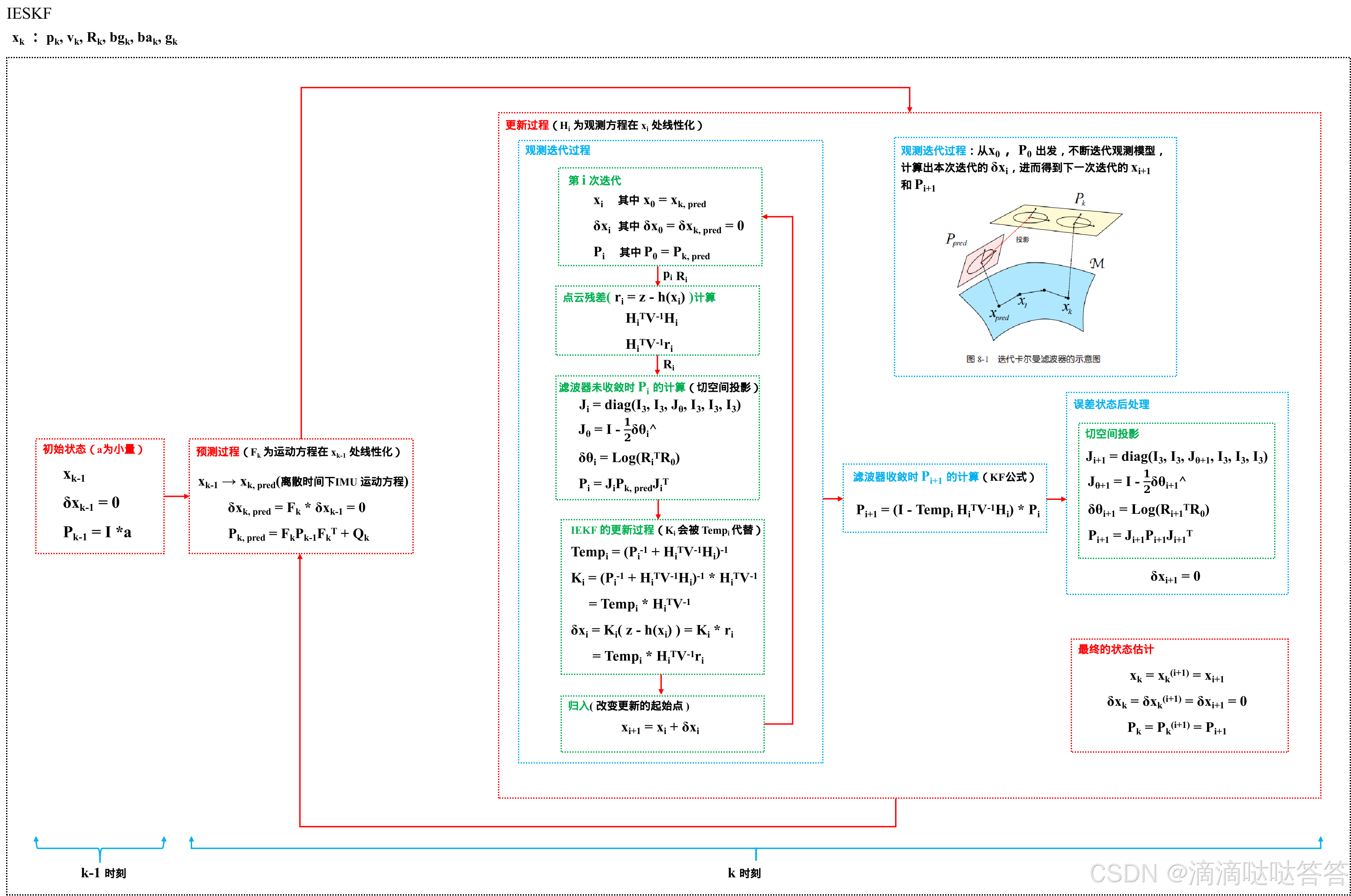
1 IESKF 的状态变量和运动过程
IESKF 的状态变量及运动过程 和 前文介绍过的 ESKF 的状态变量及运动过程完全相同,包括:① 对名义状态变量的预测 ②对误差状态变量的预测及对协方差矩阵的递推参考 《自动驾驶与机器人中的SLAM技术》ch3:惯性导航与组合导航 和 《自动驾驶与机器人中的SLAM技术》ch7:基于 ESKF 的松耦合 LIO 系统 即可。
1.1 对名义状态变量的预测
1.2 对误差状态变量的预测及对协方差矩阵的递推
为线性化后的雅可比矩阵,由于 离散时间下误差状态变量的运动方程 已经线性化,所以我们可以直接得到
。注意其等号右侧时间下标为
:
在此基础上执行 对误差状态变量的预测及对协方差矩阵的递推:
省略时间下标得:
书上的内容如下所示:

2 观测方程中的迭代过程


整个示意图如下图所示。我们从 ,
出发,不断迭代观测模型,计算出本次迭代的
,进而得到下一次迭代的
和
(在滤波器未收敛时只需进行切空间投影),最终收敛。
切空间投影:把一个切空间中的高斯分布投影到另一个切空间中。
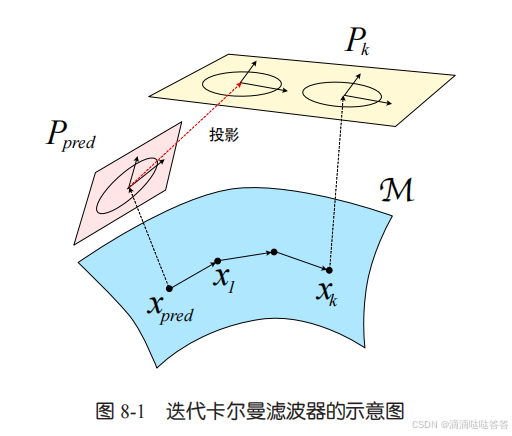
考虑当前为第 次迭代,工作点是
、
,希望计算本次的增量
,进而得到下一次迭代的
和
。
IESKF 的更新过程的表达式如下:
对于其中的 :
- 如果滤波器没有收敛,则暂不使用卡尔曼公式对
进行更新,因为下一时刻的
可以由
算得,所以可以按照那时的
,将初始分布的协方差投影过去。公式如下:
即 。
- 如果滤波器收敛,则
应该先按照卡尔曼公式进行更新,然后再使用切空间投影:
3 高维观测中的等效处理

即使用 SMV 恒等式对卡尔曼增益的公式进行变换,得:
综上,IESKF 的更新过程的表达式变为如下形式:
滤波器收敛时, 的卡尔曼更新公式变为:
下面介绍一个更加方便的表达方式。设一中间变量 ,其计算公式如下所示:
则 IESKF 的更新过程的表达式变为如下形式:
滤波器收敛时, 的卡尔曼更新公式变为如下形式:
4 NDT 和 卡尔曼滤波的联系
先给出结论:紧耦合 LIO 系统看成带 IMU 预测的高维 NDT 或 ICP,并且这些预测分布还会被推导至下一时刻。

式(7.15)左侧矩阵求逆之后得到 ,就和式(8.11)中没有预测的卡尔曼增益
一致了。只是通常的卡尔曼增益写成了矩阵形式,而 ICP 或 NDT 写成了求和形式。为了方便后文介绍 NDT LIO,我们来推导将 NDT 误差写入卡尔曼增益的形式。并且,在实验部分,我们也会参考这里的推导方式,使用求和形式的卡尔曼增益。
没有预测的卡尔曼增益公式:当没有预测时,相当于忽略了预测误差协方差 ,直接对观测误差进行加权修正,因此去掉
,公式变为
。

注意:这里点云中的第 个点
经过 IESKF 的预测位姿
(
) 的转换后,会落在目标点云中的某一个体素内,假设这个体素的正态分布参数为
。此时,该点的残差
为 转换后的点的坐标和体素中的正态分布参数中的均值之差,即
。这个点产生的平方误差为
,即
。即:
推导出以上关系后,在当前第 次迭代的过程中,我们可以向增量 NDT 里程计传入 IESKF 的预测位姿
,在 NDT 内部计算点云残差
(
)和
(
),计算完成后将这两个表示点云残差的值传递到 IESKF 中,结合预测协方差矩阵
计算得到当前迭代过程的增量
,最后将增量代入名义状态变量
,进而得到下一次迭代的
和
。
IESKF 的更新过程的流程图如下所示:
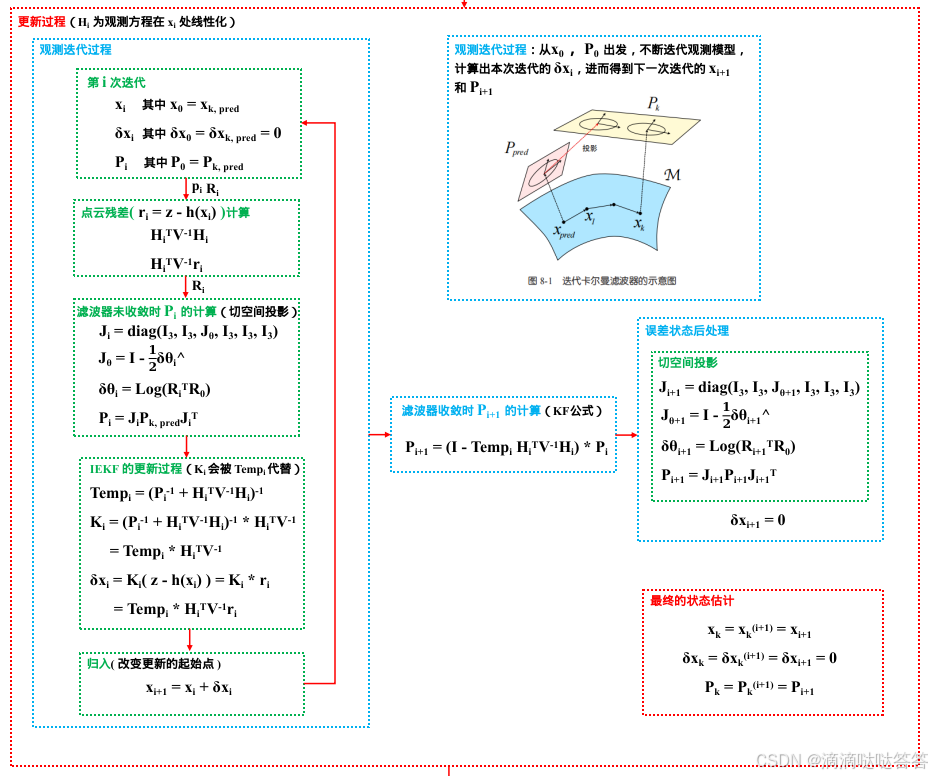
5 紧耦合 LIO 系统的主要流程
5.1 IMU 静止初始化
紧耦合 LioIEKF 类持有一个 IncNdt3d(增量 NDT,与松耦合不同)对象,一个 ESKF 对象,一个 MessageSync 对象 处理同步之后的点云和 IMU。该类处理流程非常简单:当 MeasureGroup 到达后,在 IMU 未初始化时,使用第 3 章的静止初始化来估计 IMU 零偏。初始化完毕后,先使用 IMU 数据进行预测,再用预测数据对点云去畸变,最后对去畸变的点云做配准。
void LioIEKF::ProcessMeasurements(const MeasureGroup &meas) {
LOG(INFO) << "call meas, imu: " << meas.imu_.size() << ", lidar pts: " << meas.lidar_->size();
measures_ = meas;
if (imu_need_init_) {
// 初始化IMU系统
TryInitIMU();
return;
}
// 利用IMU数据进行状态预测
Predict();
// 对点云去畸变
Undistort();
// 配准
Align();
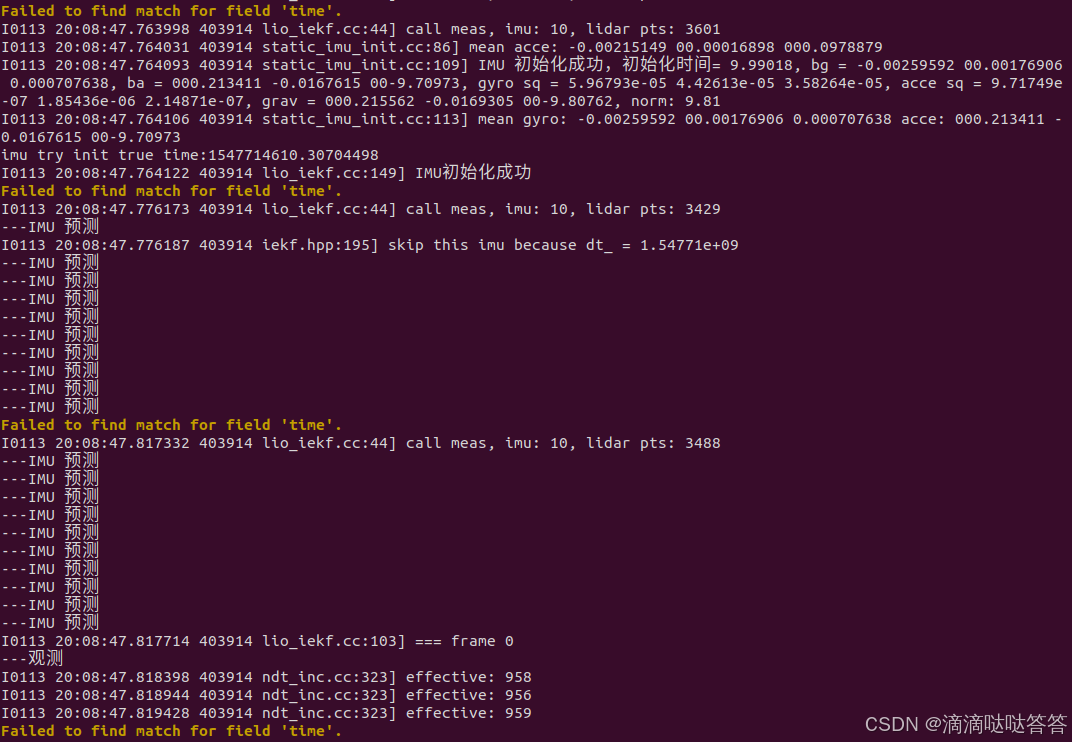
}IMU 静止初始化结果如下:

I0113 20:08:47.763998 403914 lio_iekf.cc:44] call meas, imu: 10, lidar pts: 3601
I0113 20:08:47.764031 403914 static_imu_init.cc:86] mean acce: -0.00215149 00.00016898 000.0978879
I0113 20:08:47.764093 403914 static_imu_init.cc:109] IMU 初始化成功,初始化时间= 9.99018, bg = -0.00259592 00.00176906 0.000707638, ba = 000.213411 -0.0167615 00-9.70973, gyro sq = 5.96793e-05 4.42613e-05 3.58264e-05, acce sq = 9.71749e-07 1.85436e-06 2.14871e-07, grav = 000.215562 -0.0169305 00-9.80762, norm: 9.81
I0113 20:08:47.764106 403914 static_imu_init.cc:113] mean gyro: -0.00259592 00.00176906 0.000707638 acce: 000.213411 -0.0167615 00-9.70973
imu try init true time:1547714610.30704498
I0113 20:08:47.764122 403914 lio_iekf.cc:149] IMU初始化成功5.2 ESKF 之 运动过程——使用 IMU 预测
IMU 的静止初始化与《自动驾驶与机器人中的SLAM技术》ch3:惯性导航与组合导航 中介绍的大体一致。当 MeasureGroup 到达后,在 IMU 未初始化时,调用 StaticIMUInit::AddIMU() 函数进行 IMU的静止初始化。当 IMU 初始化成功时,在当前 MeasureGroup 中完成 ESKF 中 Q, V, b_g, b_a, g_w, P 的初始化。
void LioIEKF::TryInitIMU() {
for (auto imu : measures_.imu_) {
imu_init_.AddIMU(*imu);
}
if (imu_init_.InitSuccess()) {
// 读取初始零偏,设置ESKF
sad::IESKFD::Options options;
// 噪声由初始化器估计
options.gyro_var_ = sqrt(imu_init_.GetCovGyro()[0]);
options.acce_var_ = sqrt(imu_init_.GetCovAcce()[0]);
ieskf_.SetInitialConditions(options, imu_init_.GetInitBg(), imu_init_.GetInitBa(), imu_init_.GetGravity());
imu_need_init_ = false;
LOG(INFO) << "IMU初始化成功";
}
}注意:这里有一个小地方和松耦合 LIO 不同,即协方差矩阵 P 的初始化,更加细节一些。
- ESKF 协方差矩阵初始化
void ESKF::SetInitialConditions(Options options, const VecT& init_bg, const VecT& init_ba,
const VecT& gravity = VecT(0, 0, -9.8)) {
BuildNoise(options);
options_ = options;
bg_ = init_bg;
ba_ = init_ba;
g_ = gravity;
cov_ = Mat18T::Identity() * 1e-4; // P
}
- IESKF 协方差矩阵初始化 (在
上进行了额外处理)
/// 设置初始条件
void IESKF::SetInitialConditions(Options options, const VecT& init_bg, const VecT& init_ba,
const VecT& gravity = VecT(0, 0, -9.8)) {
BuildNoise(options);
options_ = options;
bg_ = init_bg;
ba_ = init_ba;
g_ = gravity;
cov_ = 1e-4 * Mat18T::Identity();
// 设置 R 部分的协方差矩阵
cov_.template block<3, 3>(6, 6) = 0.1 * math::kDEG2RAD * Mat3T::Identity();
}
5.3 使用 IMU 预测位姿进行运动补偿
和 《自动驾驶与机器人中的SLAM技术》ch7:基于 ESKF 的松耦合 LIO 系统 中一模一样,不在介绍。
5.4 松耦合系统的配准部分
得到去畸变的点云后,将其作为 source 部分传递给增量 NDT 类 IncNdt3d ,然后开始滤波器的更新过程。在滤波器更新过程的第 次迭代过程中,首先调用IncNdt3d::ComputeResidualAndJacobians() 计算函数在 NDT 内部使用滤波器预测得到的先验位姿(首次)和更新后位姿(后续迭代)的计算点云残差
和
(和松耦合中不同,没有使用 增量 NDT 中的 IncNdt3d::AlignNdt() 配准函数迭代优化位姿)。然后将这两个表示点云残差的值传递到 IESKF 中,结合预测协方差矩阵
计算得到当前迭代过程的增量
,最后将增量代入名义状态变量
,进而得到下一次迭代的
和
直到滤波器收敛。滤波器收敛后再根据卡尔曼公式计算得到后验位姿作为当前雷达 scan 的位姿。最后根据当前雷达 scan 的位姿判断 scan 是否为关键帧,若为关键帧则添加到 local map中。在这个过程中滤波器部分和 NDT 部分是耦合的,是将点云残差写入到了滤波器的观测过程中。
IncNdt3d::AlignNdt() 配准函数:将 IESKF 的预测的先验位姿 作为初始值,在 NDT 内部进行配准操作,迭代得到优化后位姿信息。
- 配准函数中迭代遍历当前雷达扫描 scan 中的点,计算每个点的 平方误差
和 雅可比矩阵
,根据
计算得到
从而迭代更新位姿信息。
ncNdt3d::ComputeResidualAndJacobians() 计算函数:在当前第 次迭代的过程中,根据 IESKF 的预测的先验位姿
,在 NDT 内部计算
(
)和
(
)。
- 计算函数不迭代,遍历当前雷达扫描 scan 中的点,计算每个点的 平方误差
和 雅可比矩阵
,根据
和
在 NDT 内部计算
和
。
由于 NDT 点数要明显多于预测方程,这可能导致估计结果向 NDT 倾斜,我们给这里的信息矩阵 添加一个乘积因子(取 0.01),降低其权重,让更新部分更加平衡一些。
bool IncNdt3d::AlignNdt(SE3& init_pose) {
LOG(INFO) << "aligning with inc ndt, pts: " << source_->size() << ", grids: " << grids_.size();
assert(grids_.empty() == false);
SE3 pose = init_pose;
// 对点的索引,预先生成
int num_residual_per_point = 1;
if (options_.nearby_type_ == NearbyType::NEARBY6) {
num_residual_per_point = 7;
}
std::vector<int> index(source_->points.size());
for (int i = 0; i < index.size(); ++i) {
index[i] = i;
}
// 我们来写一些并发代码
int total_size = index.size() * num_residual_per_point;
for (int iter = 0; iter < options_.max_iteration_; ++iter) {
std::vector<bool> effect_pts(total_size, false);
std::vector<Eigen::Matrix<double, 3, 6>> jacobians(total_size);
std::vector<Vec3d> errors(total_size);
std::vector<Mat3d> infos(total_size);
// gauss-newton 迭代
// 最近邻,可以并发
std::for_each(std::execution::par_unseq, index.begin(), index.end(), [&](int idx) {
auto q = ToVec3d(source_->points[idx]);
Vec3d qs = pose * q; // 转换之后的q, map 坐标系下的点
// 计算qs所在的栅格以及它的最近邻栅格
Vec3i key = CastToInt(Vec3d(qs * options_.inv_voxel_size_));
for (int i = 0; i < nearby_grids_.size(); ++i) {
Vec3i real_key = key + nearby_grids_[i];
// 和 local map 产生联系
auto it = grids_.find(real_key);
int real_idx = idx * num_residual_per_point + i;
/// 这里要检查高斯分布是否已经估计
if (it != grids_.end() && it->second->second.ndt_estimated_) { // 找到了并且高斯分布是否已经估计
auto& v = it->second->second; // voxel,即 VoxelData 结构
Vec3d e = qs - v.mu_; // 残差项
// check chi2 th
double res = e.transpose() * v.info_ * e; // 平方误差项
if (std::isnan(res) || res > options_.res_outlier_th_) {
effect_pts[real_idx] = false;
continue;
}
// P259, (式 7.16)
// build residual
Eigen::Matrix<double, 3, 6> J;
J.block<3, 3>(0, 0) = -pose.so3().matrix() * SO3::hat(q);
J.block<3, 3>(0, 3) = Mat3d::Identity();
jacobians[real_idx] = J;
errors[real_idx] = e;
infos[real_idx] = v.info_; // VoxelData 中的协方差矩阵之逆
effect_pts[real_idx] = true;
} else {
effect_pts[real_idx] = false;
}
}
});
// 累加Hessian和error,计算dx
double total_res = 0;
int effective_num = 0;
Mat6d H = Mat6d::Zero();
Vec6d err = Vec6d::Zero();
for (int idx = 0; idx < effect_pts.size(); ++idx) {
if (!effect_pts[idx]) {
continue;
}
total_res += errors[idx].transpose() * infos[idx] * errors[idx];
effective_num++;
H += jacobians[idx].transpose() * infos[idx] * jacobians[idx];
err += -jacobians[idx].transpose() * infos[idx] * errors[idx];
}
if (effective_num < options_.min_effective_pts_) {
LOG(WARNING) << "effective num too small: " << effective_num;
init_pose = pose;
return false;
}
Vec6d dx = H.inverse() * err;
pose.so3() = pose.so3() * SO3::exp(dx.head<3>()); // 右乘更新
pose.translation() += dx.tail<3>();
// 更新
LOG(INFO) << "iter " << iter << " total res: " << total_res << ", eff: " << effective_num
<< ", mean res: " << total_res / effective_num << ", dxn: " << dx.norm()
<< ", dx: " << dx.transpose();
if (dx.norm() < options_.eps_) {
LOG(INFO) << "converged, dx = " << dx.transpose();
break;
}
}
init_pose = pose;
return true;
}void IncNdt3d::ComputeResidualAndJacobians(const SE3& input_pose, Mat18d& HTVH, Vec18d& HTVr) {
assert(grids_.empty() == false);
SE3 pose = input_pose;
// 大部分流程和前面的 AlignNdt()函数 是一样的,只是会把z, H, R三者抛出去而非自己处理
int num_residual_per_point = 1;
if (options_.nearby_type_ == NearbyType::NEARBY6) {
num_residual_per_point = 7;
}
std::vector<int> index(source_->points.size());
for (int i = 0; i < index.size(); ++i) {
index[i] = i;
}
int total_size = index.size() * num_residual_per_point;
std::vector<bool> effect_pts(total_size, false);
std::vector<Eigen::Matrix<double, 3, 18>> jacobians(total_size);
std::vector<Vec3d> errors(total_size);
std::vector<Mat3d> infos(total_size);
// gauss-newton 迭代
// 最近邻,可以并发
std::for_each(std::execution::par_unseq, index.begin(), index.end(), [&](int idx) {
auto q = ToVec3d(source_->points[idx]);
Vec3d qs = pose * q; // 转换之后的q
// 计算qs所在的栅格以及它的最近邻栅格
Vec3i key = CastToInt(Vec3d(qs * options_.inv_voxel_size_));
for (int i = 0; i < nearby_grids_.size(); ++i) {
Vec3i real_key = key + nearby_grids_[i];
auto it = grids_.find(real_key);
int real_idx = idx * num_residual_per_point + i;
/// 这里要检查高斯分布是否已经估计
if (it != grids_.end() && it->second->second.ndt_estimated_) {
auto& v = it->second->second; // voxel,即 VoxelData 结构
Vec3d e = qs - v.mu_; // 残差项
// check chi2 th
double res = e.transpose() * v.info_ * e; // 平方误差项
if (std::isnan(res) || res > options_.res_outlier_th_) {
effect_pts[real_idx] = false;
continue;
}
// build residual
Eigen::Matrix<double, 3, 18> J;
J.setZero();
J.block<3, 3>(0, 0) = Mat3d::Identity(); // 对p
J.block<3, 3>(0, 6) = -pose.so3().matrix() * SO3::hat(q); // 对R
jacobians[real_idx] = J;
errors[real_idx] = e;
infos[real_idx] = v.info_; // VoxelData 中的协方差矩阵之逆
effect_pts[real_idx] = true;
} else {
effect_pts[real_idx] = false;
}
}
});
// 累加Hessian和error,计算dx
double total_res = 0;
int effective_num = 0;
HTVH.setZero();
HTVr.setZero();
// 乘积因子
const double info_ratio = 0.01; // 每个点反馈的info因子
for (int idx = 0; idx < effect_pts.size(); ++idx) {
if (!effect_pts[idx]) {
continue;
}
total_res += errors[idx].transpose() * infos[idx] * errors[idx];
effective_num++;
// p314 (式8.18) (矩阵维度为18 * 18)
HTVH += jacobians[idx].transpose() * infos[idx] * jacobians[idx] * info_ratio;
// p314 (式8.20) (矩阵维度为18 * 1)
HTVr += -jacobians[idx].transpose() * infos[idx] * errors[idx] * info_ratio;
}
LOG(INFO) << "effective: " << effective_num;
}

参考
自动驾驶与机器人中的SLAM技术--第八章--紧耦合LIO系统
