当前位置：首页 > article >正文

c++ 给定欧氏平面中的一组线可以形成的三角形的数量

article 2025/1/21 20:46:13

给定欧氏平面中的一组线可以形成的三角形的数量(Number of Triangles that can be formed given a set of lines in Euclidean Plane)

给定欧氏平面上的 n 条不同直线的集合 L = {l 1 , l 2 , ………, l n }。第i 条直线由形式为 a i x + b i y = c i的方程给出。求出可以使用集合 L 中的直线形成的三角形的数量。请注意，没有两对直线会在同一点相交。
注意：此问题未提及直线不能平行，这使得问题难以解决。

例子：

输入：a[] = {1, 2, 3, 4}
b[] = {2, 4, 5, 5}
c[] = {5, 7, 8, 6}

输出：2

可以形成的三角形数量为：2

输入：a[] = {1, 2, 3, 2, 4, 1, 2, 3, 4, 5}
b[] = {2, 4, 6, 3, 6, 5, 10, 15, 20, 25}
c[] = {3, 5, 11, 10, 9, 17, 13, 11, 7, 3}

输出：30

可以形成的三角形数量为：30

朴素算法

朴素算法可以描述为：

1、从集合 L 中选取 3 条任意线。

2、现在检查是否可以使用选定的 3 条线形成三角形。这可以通过检查它们是否都是平行线来轻松完成。

3、如果可以形成三角形，则增加计数器。

时间复杂度：有n C 3 （如图：）个三元组线。对于每个三元组，我们必须进行 3 次比较才能检查任何 2 条线是否不平行，这意味着检查可以在 O(1) 时间内完成。这使得朴素算法成为 O(n 3 ),如图：。

高效算法

这也可以在 O(n log n) 中实现。高效算法背后的逻辑如下所述。

我们将集合 L 划分为各种子集。子集的形成基于斜率，即特定子集中的所有线具有相同的斜率，即它们彼此平行。

让我们考虑三个集合（例如 A、B 和 C）。对于特定集合（例如 A），属于该集合的线都是彼此平行的。如果我们有 A、B 和 C，我们可以从每个集合中挑选一条线来得到一个三角形，因为这些线都不会平行。通过制作子集，我们确保没有两条平行的线被一起挑选。

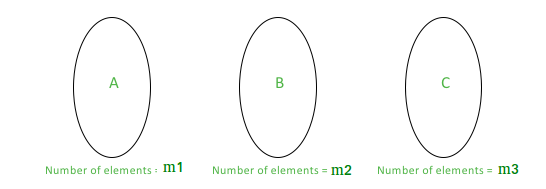
现在如果我们只有这3 个子集，

三角形的数量 =（从 A 中选取一条线的方式数量）*
（从 B 中选取一条线的方式数量）*
（从 C 中选取一条线的方式数量）
= m1*m2*m3

这里 m1 是具有第一个斜率的元素的数量（在集合 A 中）
这里 m2 是具有第一个斜率的元素的数量（在集合 B 中）
这里 m3 是具有第一个斜率的元素的数量（在集合 C 中）

类似地，如果我们有4 个子集，我们可以扩展这个逻辑来得到，
三角形数量 = m1*m2*m3 + m1*m2*m4 + m1*m3*m4 + m2*m3*m4

对于大于 3 的子集数量，如果我们有“k”个子集，我们的任务是找到每次取 3 个子集元素数量的总和。这可以通过维护一个计数数组来完成。我们创建一个计数数组，其中计数i表示第i 个平行线子集的数量。

我们逐一计算以下值。

sum1 = m1 + m2 + m3 .....
sum2 = m1*m2 + m1*m3 + ... + m2*m3 + m2*m4 + ...
sum3 = m1*m2*m3 + m1*m2*m4 + ...... m2*m3*m4 + ....
sum3 给出我们的最终答案

示例代码：

// C++ program to find the number of
// triangles that can be formed
// using a set of lines in Euclidean
// Plane
#include <bits/stdc++.h>
using namespace std;

#define EPSILON numeric_limits<double>::epsilon()

// double variables can't be checked precisely
// using '==' this function returns true if
// the double variables are equal
bool compareDoubles(double A, double B)
{
double diff = A-B;
return (diff<EPSILON) && (-diff<EPSILON);
}

// This function returns the number of triangles
// for a given set of lines
int numberOfTringles(int a[], int b[], int c[], int n)
{
//slope array stores the slope of lines
double slope[n];
for (int i=0; i<n; i++)
slope[i] = (a[i]*1.0)/b[i];

// slope array is sorted so that all lines
// with same slope come together
sort(slope, slope+n);

// After sorting slopes, count different
// slopes. k is index in count[].
int count[n], k = 0;
int this_count = 1; // Count of current slope
for (int i=1; i<n; i++)
{
if (compareDoubles(slope[i], slope[i-1]))
this_count++;
else
{
count[k++] = this_count;
this_count = 1;
}
}
count[k++] = this_count;

// calculating sum1 (Sum of all slopes)
// sum1 = m1 + m2 + ...
int sum1 = 0;
for (int i=0; i<k; i++)
sum1 += count[i];

// calculating sum2. sum2 = m1*m2 + m2*m3 + ...
int sum2 = 0;
int temp[n]; // Needed for sum3
for (int i=0; i<k; i++)
{
temp[i] = count[i]*(sum1-count[i]);
sum2 += temp[i];
}
sum2 /= 2;

// calculating sum3 which gives the final answer
// m1 * m2 * m3 + m2 * m3 * m4 + ...
int sum3 = 0;
for (int i=0; i<k; i++)
sum3 += count[i]*(sum2-temp[i]);
sum3 /= 3;

return sum3;
}

// Driver code
int main()
{
// lines are stored as arrays of a, b
// and c for 'ax+by=c'
int a[] = {1, 2, 3, 4};
int b[] = {2, 4, 5, 5};
int c[] = {5, 7, 8, 6};

// n is the number of lines
int n = sizeof(a)/sizeof(a[0]);

cout << "The number of triangles that"
" can be formed are: "
<< numberOfTringles(a, b, c, n);

return 0;
}