支持向量机SVM的应用案例

支持向量机（Support Vector Machine,SVM）是一种强大的监督学习算法，广泛应用于分类和回归任务。

基本原理

SVM的主要目标是周到一个最优的超平面，该超平面能够将不同类别的数据点尽可能分开，并且使离该超平面最近的数据点（称为支持向量）到超平面的距离最大化。这个距离称为间隔（Margin）。

• 对于线性可分的数据，SVM试图周到一个线性超平面，通过求解一个凸二次规划问题实现。
• 对于线性不可分的数据，SVM将原始特征空间映射到一个更高维的特征空间，使得在高维空间中数据变得线性可分。

信用风险评估应用场景

金融机构在评估客户的信用风险时，会考虑众多因素，比如客户的收入水平、资产状况、信用历史、债务情况等。这些因素构成了高位的输入数据。SVM可以根据历史客户数据，建立信用风险分类模型。

数据收集与准备

1. 数据收集
   明确了客户信息的维度，ID（序号）,Label（是否违约）,AGE（年龄）,GENDER（性别）,MARITAL_STATUS（婚姻状况）,MONTHLY_INCOME_WHITHOUT_TAX（税前月收入）,LOANTYPE（贷款类型）,GAGE_TOTLE_PRICE（抵押物总价）,APPLY_AMOUNT（申请贷款金额）,APPLY_TERM_TIME（贷适用期限）,APPLY_INTEREST_RATE（申请利率）,PAYMENT_TYPE（贷款还款方式）
2. 数据清洗
   检查数据中缺失值、重复值和异常值。通过对原始数据的检查，未发现明显发现重复值和异常值。

• 检查缺失值

  	print(data.isna().sum())
  

  检查结果
  
  税前收入（MONTHLY_INCOME_WITHOUT_TAX）存在缺失值的情况，因为整体样本较小，所以尽量不对存在缺失值的记录进行删除。在缺失值补充情况下，因为存在税前收入为0的同类情况，从业务角度来看，缺失的情况可以默认为0是比较合理的情况。所以对缺失值都赋值为0。此外，因为ID属性不包含任何有用信息，应予以移除。

  	data=data.drop(columns=['ID']).fillna(0)
  

• 检查重复值

  	print(data[data.duplicated(keep=False)])
  

结果：

未发现有重复数据

特征工程

1. 特征选择
   挑选对信贷分类有重要影响的特征，因为数据维度较少，通过业务经验分析，所有已有的属性都可能与信贷违约存在潜在关系，所以不进行筛选。
2. 特征编码
   对一些非数值型特征，进行编码处理，将其转换为数值型数据，以便 SVM 算法处理。

    print(data['GENDER'].unique())
	print(data['MARITAL_STATUS'].unique())
	print(data['LOANTYPE'].unique())
	print(data['PAYMENT_TYPE'].unique())  

性别、婚姻状况、贷款类型、还款方式这四个属性为非数值特征，需要进行编码处理。其中，性别、贷款类型以及还款方式都是二分类离散变量，婚姻状况是多分类离散变量。
① 对二分类离散变量处理
将性别、贷款类型以及还款方式映射为0和1。

data['GENDER'] = data['GENDER'].map({'Female': 1, 'Male': 0})
data['LOANTYPE'] = data['LOANTYPE'].map({'Frist-Hand': 1, 'Second-Hand': 0})
data['PAYMENT_TYPE'] = data['PAYMENT_TYPE'].map({'Average_Capital_Plus_Interest_Repayment': 1, 'Matching_The_Principal_Repayment': 0})

② 对多分类离散变量处理
多分类离散变量采用独热编码（one-hot）来处理，将单个特征转换为二进制的多个特征。

encoder = OneHotEncoder()
marital_status_encoded = encoder.fit_transform(data[['MARITAL_STATUS']]).toarray()
# 将单个marital_status 转换多个marital_status_i
marital_status_encoded_df = pd.DataFrame(marital_status_encoded, columns=[f'marital_status_{i}' for i in range(marital_status_encoded.shape[1])])
data = pd.concat([data.drop('MARITAL_STATUS', axis=1), marital_status_encoded_df], axis=1)

3. 特征缩放
   将数据特征进行归一化或标准化处理，将特征值映射到一定的范围内，如将数据归一化到 [0,1] 或使数据具有零均值和单位方差，以提升模型的训练效果和收敛速度。
   将数据进行标准化处理，减少数据尺度的影响。基本原理为计算输入数据 X 的均值和标准差。对于每一个特征（列），计算其均值 μ 和标准差 σ。 $$x_{scaled}=\frac{x-\mu }{\sigma }$$

   其中：

   • $x_{scaled}$ 是标准化后的特征值。
   • $x$ 是原始特征值。
   • $\mu$ 是特征的均值

X=data.drop('Label', axis=1).values
scaler=StandardScaler()
X_scaled=scaler.fit_transform(X)

建立模型

1. 划分数据集

 # 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

将准备好的数据划分为训练集和测试集，按照 8:2的比例划分。random_state 是一个可选参数，用于控制随机数生成器的状态。
当你设置 random_state 为一个特定的值42时，每次运行代码，数据集的划分结果都会相同。这是因为使用相同的 random_state 会导致随机数生成器产生相同的随机序列，从而使数据集的划分具有可重复性。

3. 选择 SVM 类型和核函数

• SVM 类型：根据信贷数据的特点和分类需求，选择合适的 SVM 类型，如线性 SVM 或非线性 SVM。如果信贷数据的特征之间呈现明显的线性可分关系，可选择线性 SVM；若数据存在复杂的非线性关系，则考虑使用基于核函数的非线性 SVM。
• 核函数：常见的核函数有线性核、多项式核、径向基函数（RBF）核等。对于信贷数据，RBF 核函数通常能较好地处理数据中的非线性关系，是一种常用的选择。
• 设置参数：设置 SVM 模型的参数，主要包括惩罚参数 C 和核函数的参数。惩罚参数 C 用于平衡模型的训练误差和复杂度，C 值越大，模型对误分类的惩罚越重，可能会导致模型过拟合；C 值越小，模型可能会欠拟合。核函数参数根据所选核函数而定，如 RBF 核的 gamma 值，gamma 值越大，模型的拟合能力越强，但也越容易过拟合。
• 模型训练：使用训练集数据对 SVM 模型进行训练，通过优化算法求解 SVM 的目标函数，得到模型的参数，确定分类超平面或决策边界。

4. 在无法明确数据分布的情况下，我们选择线性SVM和非线性SVM进行训练

 # 使用线性核的 SVM 进行分类
svm_linear = SVC(kernel='linear',probability=True)
svm_linear.fit(X_train, y_train)
print(f"Linear SVM Accuracy : {svm_linear.score(X_test, y_test)}")

线性核的预测精度为0.95053（保留5位小数）

 # 使用 RBF 核的 SVM 进行分类
svm_rbf = SVC(kernel='rbf')
svm_rbf.fit(X_train, y_train)
print(f"RBF SVM Accuracy : {svm_rbf.score(X_test, y_test)}")

非线性核RBF的预测精度为0.91519（保留5位小数）

4. GridSearchCV 网格搜索最佳参数优化模型

# 定义参数网格
param_grid = {
    'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000],
    'gamma': [0.001, 0.01, 0.1, 1, 10, 100, 1000],
    'kernel': ['rbf', 'poly', 'linear']
}

# 使用 GridSearchCV 并设置 cv
svm = SVC()
grid_search = GridSearchCV(svm, param_grid,n_jobs=-1, cv=5)  # cv = 5 表示使用 5 折交叉验证
grid_search.fit(X_train, y_train)

# 输出最佳参数组合
print(f"Best parameters: {grid_search.best_params_}")

# 使用最佳参数评估模型
best_svm = grid_search.best_estimator_
print(f"Best estimator: {best_svm}")

# 输出最佳参数组合和准确率
y_pred = best_svm.predict(X_test)
print(f"Best accuracy: {accuracy_score(y_test, y_pred)}")

Best parameters: {‘C’: 100, ‘gamma’: 0.01, ‘kernel’: ‘rbf’}
Best estimator: SVC(C=100, gamma=0.01)
Best accuracy: 0.9717314487632509

在优化后，使用C为100，gamma为0.01以及核函数为RBF的SVC分类模型训练，预测精度提升至0.97173

评价模型

ROC评估

ROC(Receiver Operating Characteristic)曲线是种用于评估二分类模型性能的可视化工具。它通过绘制真正率（True Positive Rate，TPR）与假正例率（False Positive Rate， FPR）在不同分类阈值下的关系曲线来展示模型性能。

AUC(Area Under the Curve,AUC),AUC 是ROC曲线下的面积，取值范围在0到1之间，AUC越大表示模型性能越好。

# 对测试集进行预测，获取预测概率
y_pred_prob = best_svm.predict_proba(X_test)[:, 1]
# 计算 ROC 曲线
fpr, tpr, thresholds = roc_curve(y_test, y_pred_prob)
roc_auc = auc(fpr, tpr)

# 绘制 ROC 曲线
plt.figure(figsize=(10, 6))
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

橙色曲线为优化后的SVC模型的ROC曲线，其AUC值为0.99，逼近于1，模型分类性能非常好。蓝色曲线为随机参照曲线，可以看到其AUC值为0.5。

KS评估

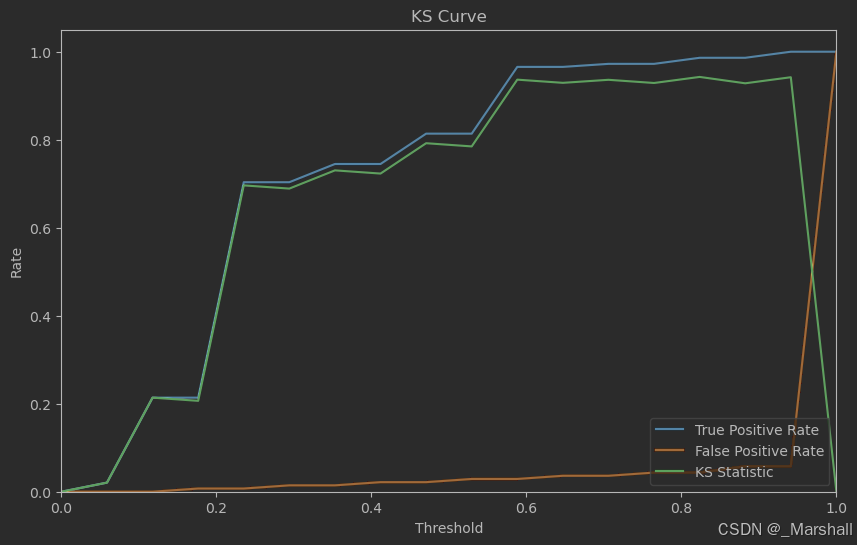
KS（Kolmogorov-Simirnov）评估是一种用于评估二分类模型区分能力的统计指标，它基于累积分布函数（Cumulative Distribution Function, CDF）的概念。KS统计量衡量了正负样本的累积分布函数之间的最大差值。
0<KS<1，一般来说，KS值越大，模型的区分能力越强。通常，在信贷风险评估领域，KS值大于0.4被认为是一个 不错的模型。

# 计算 KS 统计量
ks_statistic = np.max(np.abs(tpr - fpr))
print(f"KS Statistic : {ks_statistic}")

KS Statistic : 0.9427286356821589