理解神经网络:Brain.js 背后的核心思想
温馨提示
这篇文章篇幅较长,主要是为后续内容做铺垫和说明。如果你觉得文字太多,可以:
- 先收藏,等后面文章遇到不懂的地方再回来查阅。
- 直接跳读,重点关注加粗或高亮的部分。
放心,这种“文字轰炸”不会常有的,哈哈~ 感谢你的耐心阅读!😊
欢迎来到 brain.js 的学习之旅!
无论你是零基础的新手,还是已经有一定编程经验的开发者,这个系列都将为你提供一个系统、全面的学习路径。我们将从最基础的概念开始,逐步深入到实际应用和高级技巧,最终让你能够自信地构建和训练自己的神经网络模型。
以下是我们的学习路线图:

这一系列文章从入门到进阶,涵盖了 brain.js 的核心功能、技术细节以及实际应用场景。不仅适合初学者学习和实践,也为有一定基础的开发者提供了更多扩展和深入的思考方向。接下来,我们进入系列的第一部分:基础篇。

一、什么是神经网络?
1.1 神经网络的定义
神经网络(Neural Network),全称人工神经网络(Artificial Neural Network,ANN),是一种受生物神经系统启发的计算模型。它通过模拟人脑神经元的连接和工作方式,完成数据的处理和预测任务。
- 直观理解:神经网络就像一个会学习的系统。它通过处理输入数据,生成与之对应的输出。例如,输入一张手写数字图片,神经网络会将其分类为 0 到 9 中的某一个数字。
- 核心功能:神经网络擅长模式识别和预测。无论是语音识别、图像分类,还是文本生成,它都展现了强大的适应性和学习能力。
1.2 为什么神经网络如此强大?
传统的算法需要人为设计规则,而神经网络通过训练可以自动学习规则。这使它能够适应各种数据模式和任务场景。总结来说,神经网络是一个“通用函数近似器”,可以从数据中学习规律,并利用这些规律进行推理和预测。
1.3 举例说明:神经网络如何工作?
假设你有一组手写数字图片,神经网络的任务是识别这些数字。它的工作过程如下:
- 接收输入数据:将每张图片转化为像素矩阵,例如一个 28x28 的灰度图片会被展平为一个 784 维的向量。
- 特征提取:通过隐藏层逐步提取图片中的边缘、形状等关键信息。
- 生成输出:根据提取的特征,将图片分类为相应的数字(0 到 9)。
神经网络的强大之处在于它的“学习能力”。它能够从海量数据中提取特征并构建复杂的映射关系。它的核心结构类似于人脑,由大量的“神经元”组成,并通过“权重”连接,形成一个可以自我优化的网络。
二、神经网络的灵感来自大脑
2.1 人脑与人工神经网络的对比
神经网络的概念来源于对人脑结构和工作方式的模拟。人脑是由大约 860亿个神经元 和 数百万亿个突触 组成的复杂网络。它通过这些神经元的连接和协作,完成思维、学习和决策等复杂任务。
人工神经网络(Artificial Neural Network,ANN)通过数学建模,抽象出人脑的部分功能。尽管人工神经网络远不及人脑复杂,但它能够在特定任务中表现得非常出色。
以下是人脑和人工神经网络的一些对比:
| 特性 | 人脑 | 人工神经网络 |
|---|---|---|
| 基本单元 | 神经元(Neuron) |
人工神经元(Node) |
| 信息传递方式 | 电化学信号通过突触传播 | 数值信号通过权重传播 |
| 学习能力 | 通过强化学习调整突触连接强度 | 通过训练调整权重和偏置 |
| 灵活性 | 高度灵活,能处理多任务 | 通常针对特定任务设计,灵活性较低 |
| 能耗 | 高效低耗能 | 能耗高,尤其在大规模训练时 |
2.2 生物神经元的工作原理
生物神经元由以下三个主要部分组成:
- 树突(
Dendrite):接收其他神经元传来的信号。 - 细胞体(
Soma):对接收到的信号进行整合和处理,并决定是否激活神经元。 - 轴突(
Axon):如果神经元被激活,轴突将信号传递给下一个神经元。
信号传播过程:
- 树突接收到多个信号,并传递到细胞体。
- 如果信号强度超过某个阈值,神经元会“激活”,产生动作电位。
- 动作电位通过轴突传播到突触,影响下一个神经元。
2.3 生物神经元的工作原理
人工神经元是对生物神经元的数学抽象模型,它通过以下方式工作:
-
接收输入信号(
Input):每个输入信号代表一个特征值,例如房价预测中的面积或房间数。 -
加权求和(
Weighted Sum):输入信号会根据重要性赋予不同的权重(Weight)。权重值越大,表示信号对最终结果的影响越大。输入信号会根据重要性赋予不同的权重(
Weight)。权重值越大,表示信号对最终结果的影响越大。
z = ∑ i = 1 n w i ⋅ x i + b z = \sum_{i=1}^{n} w_i \cdot x_i + b z=i=1∑nwi⋅xi+b
其中:xi:第i个输入信号wi:对应的权重b:偏置(Bias),用于调整计算结果
-
激活函数(
Activation Function):加权求和结果会通过一个激活函数,决定神经元是否激活,以及激活后的输出值。 -
输出信号(
Output):激活函数的结果被传递到下一层神经元,直到输出层。
2.4 从生物神经元到人工神经元的转化
| 生物神经元部分 | 对应的人工神经元组件 | 功能 |
|---|---|---|
树突(Dendrite) |
输入信号 | 接收外界输入数据,传递到神经元中处理 |
细胞体(Soma) |
加权求和和激活函数 | 处理输入信号,并根据阈值决定是否激活 |
轴突(Axon) |
输出信号 | 将激活后的信号传递给下一层的神经元 |
人工神经元的设计灵感虽然来源于生物神经元,但它的目标是高效计算和任务专用化,而不是完全复制生物神经元的复杂性。通过输入信号、权重、偏置和激活函数的协作,人工神经元能够处理复杂的数据模式并生成输出。
三、人工神经网络的基础结构
人工神经网络由多个神经元按照层级结构排列而成,通常包括以下三个部分:输入层、隐藏层 和 输出层。每一层都有特定的功能,它们协同工作以实现数据处理和任务预测。
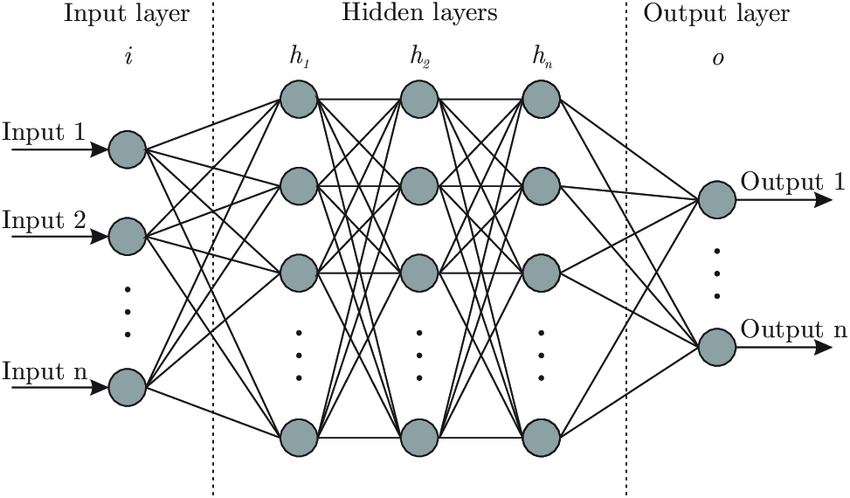
3.1 输入层(Input Layer)
作用:输入层是神经网络的起点,用于接收外部数据,并将这些数据传递给网络的下一层。
- 每个输入节点对应一个特征值。例如,在房价预测中,特征可能包括面积、房间数、地理位置等。
- 输入层本身不对数据进行任何处理,只是将数据作为信号传递到隐藏层。
假设我们有以下数据用于预测房价:
- 面积:120 平方米
- 房间数:3
- 距市中心距离:5 公里
这些数据会作为输入信号传递到网络中。
3.2 隐藏层(Hidden Layer)
作用:隐藏层是神经网络的核心计算部分,用于提取数据特征并执行复杂的数学运算。
- 隐藏层节点会接收来自上一层的输入信号,经过权重计算和激活函数处理后,将结果传递给下一层。
- 隐藏层的数量和每层节点数可以根据问题的复杂性调整。
隐藏层的计算过程:
-
对输入信号进行加权求和:
z = ∑ i = 1 n w i ⋅ x i + b z = \sum_{i=1}^{n} w_i \cdot x_i + b z=i=1∑nwi⋅xi+bwi:输入信号的权重xi:输入信号b:偏置,用于调整计算结果
-
应用激活函数:
a = f ( z ) a = f(z) a=f(z)f:激活函数,用于引入非线性,使网络能够学习复杂的模式。
在房价预测中,隐藏层中的一个节点可能专注于“面积”和“房间数”之间的关系,而另一个节点可能关注“距离市中心”和“房价”的关系。通过多层隐藏层的计算,神经网络能够提取到输入数据中的深层次特征。
3.3 输出层(Output Layer)
作用:输出层是神经网络的终点,用于生成最终结果。
- 输出的形式取决于任务类型:
- 分类任务:输出层通常包含多个节点,每个节点表示一个类别的概率。
- 回归任务:输出层通常只有一个节点,表示连续值的预测结果。
在手写数字识别中,输出层有 10 个节点,表示数字 0-9 的概率。例如:输出层结果:[0.1, 0.05, 0.8, 0.05, ...],这里第 3 个节点的值为 0.8,表示神经网络预测输入图片是数字“2”。
在房价预测中,输出层可能直接输出房价,例如 200 万元。
3.4 激活函数(Activation Function)
作用:激活函数是每个节点的“开关”,决定神经元是否被激活,以及如何传递信号到下一层。
- 如果没有激活函数,神经网络只能处理简单的线性关系,无法应对复杂的非线性问题。
- 数学意义:激活函数引入非线性,使神经网络具备学习复杂映射关系的能力。
常见激活函数:
-
Sigmoid:
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1 + e^{-x}} f(x)=1+e−x1
将输出限制在 (0, 1) 范围内,适合二分类任务。 -
ReLU(Rectified Linear Unit):
f ( x ) = max ( 0 , x ) f(x) = \max(0, x) f(x)=max(0,x)
简单高效,广泛用于隐藏层节点。 -
Tanh(双曲正切函数):
f ( x ) = e x − e − x e x + e − x
