当前位置：首页 > article >正文

deep generative model stanford lecture note2 --- autoregressive

article 2025/2/3 5:31:18

1 Introduction

在note1 已经明确了生成模型，是通过概率分布来拟合数据，这个部分采用自回归的模型结构来拟合数据。主要任务包括：选择什么样的自回归模型结构和设计什么样的loss函数来让模型收敛。
自回归模型结构的理论基础还是贝叶斯概率结合马尔可夫假设(未来状态只和历史的有限个状态相关)：
$p(x_1,x_2,x_3,...,x_n)=p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)...p(x_n|x_1,...,x_{n-1})$

2 模型结构

2.1 FVSBN(Fully Visible Sigmoid Belief Network)

直接从贝叶斯概率公式延伸，用简单的逻辑回归来实现贝叶斯概率网络
在这里插入图片描述
最原始的结构：
$p(x_n|x_1,x_2,...,x_{n-1})=\sigma(\alpha_0+\sum_1^n \alpha_i x_i)$

作为算法我们需要研究一下这种方法所需要的参数数量，假定有n个状态变量：
$\hat{x}_1$ 参数是 $\alpha_0$ , $\hat{x}_2$ 的参数是 $\alpha_0, \alpha_1$ ,所以一共有 $1+2+...+n=\frac{(n+1)n}{2}$ 个alpha变量，如果每个alpha是d维的，则一共有 $\frac{(n+1)n}{2}d$ 个参数。

2.2 NADE(Neural Autoregressive Density Estimation)

FVSBN 这里有几个问题是很好处理的：
1）计算复杂度是o(n^2)的，对于稍微复杂一点的问题，如mnist(n=784)也是不能接受的；
2）可以将早期神经网络的隐藏层引入进去；
$\begin{aligned} h_i &=\sigma([w_1,w_2,...,w_{i-1}] \begin{bmatrix} x_1 \\ x_2 \\ ... \\ x_{i-1} \end{bmatrix}) \\ \hat{x}_n & = \sigma(\alpha_i h_i+b_i) \end{aligned}$

在这里插入图片描述
重新来统计一下参数量：
隐藏层有nd个参数，输出层有nd个参数，参数量是O(nd)相对于之前提升明显。

输出状态的类别大于2
在nade的基础上，如果需要输出多个类别，比如说255个灰度图，那么在输出层使用softmax就可以：
$Softmax(\vec{a})=(\frac{e^{a_1}}{\sum_i e^{a_i}},\frac{e^{a_2}}{\sum_i e^{a_i}},...,\frac{e^{a_n}}{\sum_i e^{a_i}}$
输出连续分布
如果输出的状态变量是连续变量，这个时候需要模型输出均值和方差。
$\hat{x}_i=(\mu_i^1,...,\mu_i^k,\sigma_i^1,...,\sigma_i^k)=\alpha_i h_i + b_i$

2.3 autoencoder

NADE 从网络结构上来说就是将MLP根据先验知识进行了mask，但是这样网络结构太复杂了。
在这里插入图片描述

2.4 NLP 领域的RNN

在transformer 一统之前，在NLP领域，自回归生成模型的主流模型是RNN。
$\begin{aligned} h_{t+1} &=tanh(w_{hh}h_t + w_{xh}x_{t+1}) \\ h_0 & = b_0 \\ o_{t+1} & = w_{hy}h_{t+1} \end{aligned}$
在这里插入图片描述

2.5 图像领域的pixCNN

类似于MADE, 对输入的图像在输入层的时候添加带mask的卷积。
在这里插入图片描述

2.6 声音领域的wavenet

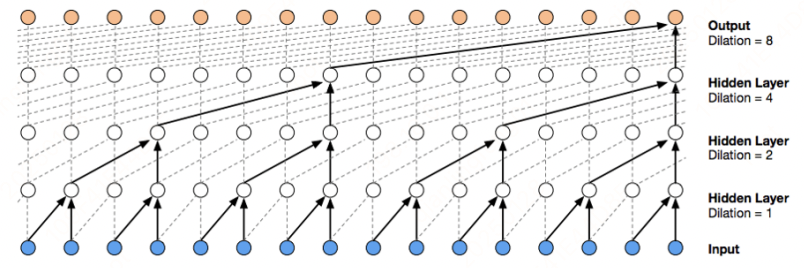
在这里插入图片描述

3 参数迭代

3.1 用熵比较分布的距离

先来看熵的定义,直觉上来说，概率越低的数据需要的比特越多，统计一下整个数据所需要的比特数就行了。有两种方式可以进行统计，全部统计和分层抽样统计。
$\begin{aligned} -E_{x~p_{data}}logp_{data}(x) &=-\frac{1}{D}\sum logp_{data}(x) \\ & = -\sum p_{data}(x)logp_{data}(x) \end{aligned}$

现在有两个分布，如果需要比较一下两个分布的差异，从熵的角度就一目了然了。如果他们的概率分布接近，那么他们的熵就应该很接近。
$\begin{aligned} D(p||q) &=E_{x-p}(logp(x)-logq(x)) \\ &=E_{x-p}log\frac{p(x)}{q(x)} \\ & = \sum_x p(x)log\frac{p(x)}{q(x)} \\ \end{aligned}$

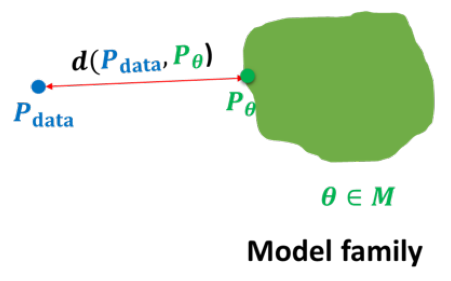
对于数据拟合问题：
$\begin{aligned} D(p_{data}||p_{\theta}) & = \sum_x (p_{data}logp_{data}-p_{data}logp_{\theta})\\ & = const -\sum_x p_{data}logp_{\theta} \end{aligned}$
为了将KL散度尽量小，需要将 $\sum_x p_{data}logp_{\theta}$ 尽量大，这也是极大似然。极大似然可以用采样的角度来理解，也就是将所有数据统计，然后再取平均；或者进行抽样采样，并且加上对应的分布概率。
$\begin{aligned} E_{x-p_{data}}[logP_{\theta}(x)] & = \sum_x p_{data}logp_{\theta} \\ & = \frac{1}{D}\sum_{x \in D} logP_{\theta}(x) \end{aligned}$

在这里插入图片描述
这里还有个问题 $p_{data}$ 是全体数据，模型训练的时候，只能通过monte carlo方法进行估计。

3.2 极大似然解析解

例如说硬币问题,假定使用概率分布
$P_{\theta}(x)= \begin{cases} \theta & \text{if } x=H \\ 1-\theta & \text{else } x=T \end{cases}$

后验结果：D={H,H,T,H,T}
按照我们的极大似然的思路, 后面下角标表示状态维度，上角标表示不同的样本。
$\begin{aligned} \frac{1}{D}\sum_{x \in D} logP_{\theta}(x) &=\frac{1}{5}\sum_x logP_{\theta}(x_1) +logP_{\theta}(x_2)+...+logP_{\theta}(x_5)\\ & = \frac{1}{5}\sum_x logP_{\theta}(x^{(1)}) P_{\theta}(x^{(2)}) ...P_{\theta}(x^{(5)}) \\ & = \frac{1}{5}\sum_xlog(\theta \theta (1-\theta) \theta (1-\theta)) \end{aligned}$
变成了要搞一个 $\theta$ 使得这个KL散度最大,这个问题比较简单，可以通过一阶导=0的方式来得到解析解，这里是 $\theta=0.6$

3.3 极大似然估计数值解

对于复杂问题，现在是没有解析解，那么这个时候只能先把loss(KL散度)计算出来，然后用auto-diff等工具进行梯度回传，来更新参数 $\theta$ .
对于一个维度是n的变量，根据前面提到的贝叶斯概率
$\begin{aligned} P(x_1,x_2,...,x_n)& =p(x_1)p(x_2|x_1)...p(x_n|x_1,x_2,...,x_{n-1}) \\ & = \prod_{i=1}^n p(x_i|x_{<i};\theta_i) \end{aligned}$

前面我们知道
$\begin{aligned} \frac{1}{D}\sum_{x \in D} logP_{\theta}(x) & = \frac{1}{m}\sum_x logP_{\theta}(x^{(1)}) P_{\theta}(x^{(2)}) ...P_{\theta}(x^{(m)}) \\ & = \frac{1}{m}\sum_x log\prod_m P_{\theta}(x^{(i)}) \end{aligned}$

我们在定义极大似然的loss的时候，直接用
$\begin{aligned} L(\theta, D) &= \prod_{j=1}^m P_{\theta}(x^{(j)}) \\ & = \prod_{j=1}^m \prod_{i=1}^n P_{\theta}(x_i^{(j)}|x_{<i}^{(j)};\theta_i) \\ \frac{1}{D}\sum_{x \in D} logP_{\theta}(x) & = \frac{1}{m}\sum_{j=1}^m log \prod_{i=1}^n P_{\theta}(x_i^{(j)}|x_{<i}^{(j)};\theta_i) \\ & = \frac{1}{m}\sum_{j=1}^m\sum_{i=1}^n log P_{\theta}(x_i^{(j)}|x_{<i}^{(j)};\theta_i) \end{aligned}$

用sgd的方法进行参数迭代:
$\begin{aligned} \nabla \frac{1}{D}\sum_{x \in D} logP_{\theta}(x) & = \frac{1}{m}\sum_{j=1}^m\sum_{i=1}^n \nabla log P_{\theta}(x_i^{(j)}|x_{<i}^{(j)};\theta_i) \end{aligned}$