半导体器件与物理篇6 MESFET
金属-半导体接触
MESFET与MOSFET的相同点:它们的电压电流特性相似。都有源漏栅三极,强反型,漏极加正向电压,也会经历线性区、夹断点、饱和区三个阶段。
MESFET与MOSFET的不同点:在器件的栅电极部分,MESFET利用金属-半导体的整流接触取代了MOSFET的MOS结构。而在源极与漏极部分,MESFET以欧姆接触取代MOSFET中的p-n结。
金半场效应晶体管的优点:热稳定性好;由于使用GaAs或InP等高电子迁移率材料,具有高开关速度和截止频率;响应速度快
MESFET的特点:大部分的MESFET是用n型Ⅲ-V族化合物半导体制成的(如砷化镓),因为它们具有较高的电子迁移率,可以减小串联电阻并且具有较高的饱和速度而使得截止频率增高。
势垒电势
金-半接触可以分为两种形式,分别是 整流性和非整流的欧姆性。
金属-半导体接触的结构示意图:

独立的技术与独立的n型半导体的能带图:

当金属与半导体紧密接触时,两种不同材料的费米能级在热平衡时应相同。此外,真空能级也必须是连续的。这两项要求影响下的热平衡时金属-半导体紧密接触时的能带图如下:

理想情况下的势垒高度根据半导体的类型有所区别。p型半导体的势垒高度的表达式为:
q
ϕ
B
p
=
E
g
−
(
q
ϕ
m
−
q
x
)
q\phi_{Bp}=E_g-(q\phi_m-qx)
qϕBp=Eg−(qϕm−qx);n型半导体的势垒高度表达式为:
q
ϕ
B
n
=
q
ϕ
m
−
q
x
q\phi_{Bn}=q\phi_m-qx
qϕBn=qϕm−qx。其中
q
x
qx
qx未电子亲和力。
可见势垒高度为金属功函数与电子亲和力之差。
势垒高度与内建电势的关系为: V b i = q ( ϕ B n − V n ) = ψ n − ψ p = k T q l n N A N D n i 2 V_{bi}=q(\phi_{Bn}-V_n)=\psi_n-\psi_p=\frac{kT}{q}ln\frac{N_AN_D}{n_i^2} Vbi=q(ϕBn−Vn)=ψn−ψp=qkTlnni2NAND
同样的,我们也可以通过n型和p型的势垒高度推导禁带宽度: E g = q ( ϕ b p + ϕ B n ) E_g=q(\phi_{bp}+\phi_{Bn}) Eg=q(ϕbp+ϕBn)
势垒高度与内建电势的关系为: V b i = q ( ϕ B n − V n ) = ψ n − ψ p = k T q l n N A N D n i 2 V_{bi}=q(\phi_{Bn}-V_n)=\psi_n-\psi_p=\frac{kT}{q}ln\frac{N_AN_D}{n_i^2} Vbi=q(ϕBn−Vn)=ψn−ψp=qkTlnni2NAND
V n q V_nq Vnq为导带底与费米能级间的距离,等于导带底与费米能级之差: V n q = E c − E F = k T ⋅ l n ( N c N D ) V_nq=E_c-E_F=kT\cdot ln(\frac{N_c}{N_D}) Vnq=Ec−EF=kT⋅ln(NDNc)
对于一个热平衡状态的金属、半导体,我们将对其施加一个可正可负的电压。当我们不知道电压的正负时,我们使用V表示外加偏压;当已知为正向偏压时,我们使用 V F V_F VF,F表示forward;当已知负向偏压时,我们使用 V R V_R VR,R表示reverse。
讨论不同偏压下,势垒的变化
第一种:当偏压为零时,即处于热平衡的情况下,两种材料有相同的费米能级。金属与半导体欧姆接触处的势垒高度如图:

第二种:在金属上施以相对于n型半导体为正的偏压时,半导体到金属的势垒高度将变小;由于势垒降低,使得电子更易由半导体进入金属。金属与半导体欧姆接触处的势垒高度如图:

第三种:当施以一反向偏压,将使得势垒提高了
V
R
V_R
VR。因此对电子而言,将变得更难从半导体进入金属中。金属与半导体欧姆接触处的势垒高度如图:

对p型半导体而言,可以获得相似的结果,不过极性相反:

电场分布
已知,任何两种材料“紧密接触”时满足费米能级相同,且真空能级连续。
电场分布为:
∣
E
(
x
)
∣
=
q
N
D
(
W
−
x
)
ε
s
=
E
m
−
q
N
D
ε
s
x
|E(x)|=\frac{qN_D(W-x)}{\varepsilon_s}=E_m-\frac{qN_D}{\varepsilon_s}x
∣E(x)∣=εsqND(W−x)=Em−εsqNDx
电场最大值为:
E
m
=
q
N
D
W
ε
s
E_m=\frac{qN_DW}{\varepsilon_s}
Em=εsqNDW
电容电压(C-V)关系
已知内建电压与外加偏压之差,与电场最大值的关系:
V
b
i
−
V
=
E
m
W
2
V_{bi}-V=\frac{E_mW}{2}
Vbi−V=2EmW
将
E
m
E_m
Em代入得到:
V
b
i
−
V
=
q
N
D
W
2
2
ε
s
V_{bi}-V=\frac{qN_DW^2}{2\varepsilon_s}
Vbi−V=2εsqNDW2
由此可以得到耗尽区宽度的表达式:
W
=
2
ε
s
(
V
b
i
−
V
)
q
N
D
W=\sqrt{\frac{2\varepsilon_s(V_{bi}-V)}{qN_D}}
W=qND2εs(Vbi−V)
由耗尽区的电容特性,可以得到耗尽区表面的电荷量为:
Q
s
c
=
q
N
D
W
=
2
q
N
D
ε
s
(
V
b
i
−
V
)
(
C
/
c
m
2
)
Q_{sc}=qN_DW=\sqrt{2qN_D\varepsilon_s(V_{bi}-V)} (C/cm^2)
Qsc=qNDW=2qNDεs(Vbi−V)(C/cm2)
对正向偏压,V为正
V
F
V_F
VF;对反向偏压,V为负
V
R
V_R
VR。
耗尽区等效的电容大小为: C = ∣ ∂ Q s c ∂ V ∣ = ε s W = s q r t q ε s N D 2 ( V b i − V ) C=|\frac{\partial Q_{sc}}{\partial V}|=\frac{\varepsilon_s}{W}=sqrt{\frac{q\varepsilon_sN_D}{2(V_{bi}-V)}} C=∣∂V∂Qsc∣=Wεs=sqrt2(Vbi−V)qεsND
将上式变换,得到:
1
C
2
=
2
(
V
b
i
−
V
)
q
ε
s
N
D
\frac{1}{C^2}=\frac{2(V_{bi}-V)}{q\varepsilon_sN_D}
C21=qεsND2(Vbi−V)
由以上式子,再结合坐标图可以得到截距和斜率。
我们将斜率表示为
d
(
1
C
2
/
d
V
d(\frac{1}{C^2}/dV
d(C21/dV,再由斜率
d
(
1
C
2
/
d
V
=
2
q
ε
s
N
D
d(\frac{1}{C^2}/dV=\frac{2}{q\varepsilon_sN_D}
d(C21/dV=qεsND2可以得到用于掺杂的施主杂质浓度为:
N
D
=
2
q
ε
s
⋅
−
1
d
(
1
C
2
/
d
V
)
N_D=\frac{2}{q\varepsilon_s}\cdot \frac{-1}{d(\frac{1}{C^2}/dV)}
ND=qεs2⋅d(C21/dV)−1
再由截距等于
2
q
ε
s
N
D
V
b
i
\frac{2}{q\varepsilon_sN_D}V_{bi}
qεsND2Vbi可以得到
V
b
i
V_{bi}
Vbi
最后由
V
b
i
=
ϕ
B
n
−
V
n
V_{bi}=\phi_{Bn}-V_n
Vbi=ϕBn−Vn和
V
n
=
E
C
−
E
F
q
=
k
T
q
l
n
N
C
N
D
V_n=\frac{E_C-E_F}{q}=\frac{kT}{q}ln\frac{N_C}{N_D}
Vn=qEC−EF=qkTlnNDNC,可以求得势垒高度
ϕ
B
n
\phi_{Bn}
ϕBn
该小节的习题见例1。
肖特基势垒(金属-半导体接触而成)
肖特基势垒:指一具有大的势垒高度(即 ϕ B n 或 ϕ B p > > k T \phi_{Bn}或\phi_{Bp}>>kT ϕBn或ϕBp>>kT),以及掺杂浓度比导带或价带上态密度低的金属-半导体接触。
肖特基势垒的特点:电流的传导主要由多数载流子来完成,这与由少数载流子来进行电流传导的p-n结不同。
肖特基二极管基本被视为单极性器件,即主要由一种载流子来主导导通的过程
肖特基势垒的传导机制:对工作在适当温度(如300K)下的肖特基二极管而言,其主要传导机制是半导体中多数载流子的热电子发射越过电势势垒而进入金属中。
热平衡、正向偏压和反向偏压下的肖特基二极管的结处的能带图如下:

肖特基势垒下的电流密度的计算
热平衡时
热平衡时的载流子浓度为:
n
t
h
=
N
C
e
x
p
(
−
q
ϕ
B
n
k
T
)
n_{th}=N_Cexp(-\frac{q\phi_{Bn}}{kT})
nth=NCexp(−kTqϕBn)
其中势垒高度
ϕ
B
n
=
E
C
−
E
F
\phi_{Bn}=E_C-E_F
ϕBn=EC−EF,而
E
C
−
E
F
E_C-E_F
EC−EF可以用杂质浓度与本征载流子浓度表示,
E
C
−
E
F
=
k
T
q
l
n
(
N
A
N
D
n
i
2
)
E_C-E_F=\frac{kT}{q}ln(\frac{N_AN_D}{n_i^2})
EC−EF=qkTln(ni2NAND)
从金属流向半导体的电流密度与从半导体流向金属的电流密度相等,且与热平衡时的载流子浓度成正比:
∣
J
m
→
s
∣
=
∣
J
s
→
m
∣
∝
n
t
h
|J_{m\rightarrow s}|=|J_{s\rightarrow m}| \propto n_{th}
∣Jm→s∣=∣Js→m∣∝nth
由正比关系,代入比例系数C1和
n
t
h
n_{th}
nth的表达式可以得到:
∣
J
m
→
s
∣
=
∣
J
s
→
m
∣
=
C
1
⋅
N
C
e
x
p
(
−
−
ϕ
B
n
k
T
)
|J_{m\rightarrow s}|=|J_{s\rightarrow m}| = C1 \cdot N_Cexp(-\frac{-\phi_{Bn}}{kT})
∣Jm→s∣=∣Js→m∣=C1⋅NCexp(−kT−ϕBn)
正向偏压时
当外加正向偏压
V
F
V_F
VF时,跨越势垒的静电势差降低,因此表面的电子浓度增加
。得到电子浓度为:
n
=
N
C
e
x
p
[
−
(
q
ϕ
B
n
−
V
F
)
k
T
]
n=N_Cexp[-\frac{(q\phi_{Bn}-V_F)}{kT}]
n=NCexp[−kT(qϕBn−VF)]
此时金属与半导体间互相流向的电流密度将不再相等。
因为是正向偏压,因此得到半导体流向金属的电流密度为:
J
=
∣
J
s
→
m
∣
=
J
S
[
e
x
p
(
q
V
k
T
)
−
1
]
J=|J_{s\rightarrow m}|=J_S[exp(\frac{qV}{kT})-1]
J=∣Js→m∣=JS[exp(kTqV)−1]
同理,对反向偏压的情况而言,其净电流的表示式基本与上述的表达式相同,只是其的
V
F
V_F
VF被替换成
−
V
R
-V_R
−VR。
我们令 C 1 N C = A ∗ T 2 C_1N_C=A^*T^2 C1NC=A∗T2,其中 A ∗ A^* A∗为“有效理查逊常数”,它的取值有如下规律:
| – | n型半导体 | p型半导体 |
|---|---|---|
| Si | 110 | 32 |
| GaAs | 8 | 74 |
金属与n型半导体接触导致的少子电流
当半导体为n型时,金属承担了p型半导体的职责,故我们将从金属流向半导体的电流密度设为
J
p
J_p
Jp。得到:
∣
J
m
→
s
∣
=
J
p
=
J
p
0
[
e
x
p
(
q
V
k
T
)
−
1
]
|J_{m\rightarrow s}|=J_p=J_{p0}[exp(\frac{qV}{kT})-1]
∣Jm→s∣=Jp=Jp0[exp(kTqV)−1]
其中
J
p
0
=
q
D
p
n
i
2
L
p
N
D
J_{p0}=\frac{qD_pn_i^2}{L_pN_D}
Jp0=LpNDqDpni2
其中
J
S
J_S
JS表示饱和电流密度:
J
S
=
A
∗
T
2
e
x
p
(
−
q
ϕ
B
n
k
T
)
J_S=A^*T^2exp(-\frac{q\phi_{Bn}}{kT})
JS=A∗T2exp(−kTqϕBn)
在正常工作情况下,少数载流子电流大小比多数载流子电流少了几个数量级(并不是没有少数载流子)。因此,肖特基二极管被视为单极性器件,亦即主要由一种载流子来主导导通的过程。
该小结对应例2。
欧姆接触ohmic contact
欧姆接触的定义:当金属-半导体接触的接触电阻相对于半导体主体或串联电阻可以忽略不计时,这种接触即为欧姆接触。
欧姆接触的一个指标为特定接触电阻 R C R_C RC,其定义为: R C = ( ∂ J ∂ V ) V = 0 − 1 R_C=(\frac{\partial J}{\partial V})^{-1}_{V=0} RC=(∂V∂J)V=0−1
对于低掺杂浓度的金属-半导体接触而言,
R
C
=
k
q
A
∗
T
e
x
p
(
q
ϕ
B
n
k
T
)
R_C=\frac{k}{qA^{*}T}exp(\frac{q\phi_{Bn}}{kT})
RC=qA∗Tkexp(kTqϕBn)
对于高掺杂浓度的金属-半导体接触而言,
R
C
∝
e
x
p
(
4
m
n
ε
s
ϕ
B
n
N
D
h
)
R_C \propto exp(\frac{4\sqrt{m_n\varepsilon_s}\phi_{Bn}}{\sqrt{N_D}h})
RC∝exp(NDh4mnεsϕBn)
其中
c
2
=
4
m
n
ε
s
/
h
c_2=4\sqrt{m_n\varepsilon_s}/h
c2=4mnεs/h。可见,在隧穿范围内特定接触电阻与杂质浓度强烈相关并且以
ϕ
B
n
/
N
D
\phi_{Bn}/\sqrt{N_D}
ϕBn/ND为因子成指数变化。
金半场效应晶体管MESFET
MESFET的结构:MESFET共具有三个金属-半导体接触,一个肖持基接触作为栅极以及两个当作源极与漏极的欧姆接触。
MESFET的特点:大部分的MESFET是用n型HI-V族化合物半导体制成的(如砷化镓),因为它们具有较高的电子迁移率,可以减小串联电阻并且具有较高的饱和速度而使得截止频率增高。
对于MOSFET而言,若栅极长度(L)为0.5um,栅极宽度(Z)为300μm,则称之为0.5um*300um的器件。其电流操控能力直接正比于栅极宽度Z,因为沟道电流的截面积与Z成正比。
MESFET的重要参数包括:栅极宽度Z;栅极长度L;外延层厚度a;沟道长度 L g s L_{gs} Lgs和 L g d L_{gd} Lgd(gs表示gate and source,gd表示gate and drain)
对于沟道为n型材料的器件称为n沟道MESFET。因为n沟道器件具有较高的电子迁移率,所以在大多数的应用中是采用n沟道MESFET而非p沟道MESFET。
沟道电阻是MESFET的另一个重要参数,其表达式为:
R
=
ρ
L
A
=
L
Q
μ
n
N
D
Z
(
a
−
W
)
R=\rho \frac{L}{A}=\frac{L}{Q\mu_nN_DZ(a-W)}
R=ρAL=QμnNDZ(a−W)L
电流流动的截面积A;肖特基势垒的耗尽区宽度W。
耗尽型MESFET
V G = 0 V_G=0 VG=0时漏极电压与漏极电流的关系
在 V D V_D VD作为正向电压很小时,晶体管处于线性区,其漏极电流: I D V D R I_D\frac{V_D}{R} IDRVD
当
V
D
V_D
VD逐渐上升时,会来到夹断点点。此时会使漏极处的耗尽区宽度
W
=
a
W=a
W=a
由
V
b
i
−
V
=
E
m
W
2
=
q
N
D
W
2
2
ε
s
V_{bi}-V=\frac{E_mW}{2}=\frac{qN_DW^2}{2\varepsilon_s}
Vbi−V=2EmW=2εsqNDW2,且已知
W
=
a
,
V
D
=
−
V
D
s
a
t
W=a,V_D=-V_{Dsat}
W=a,VD=−VDsat,可以代入计算得到:
V
D
s
a
t
=
N
D
a
2
2
ε
s
−
V
b
i
V_{Dsat}=\frac{N_Da^2}{2\varepsilon_s}-V_{bi}
VDsat=2εsNDa2−Vbi
在此漏极电压下,源极和漏极将会被夹断或说是被反向偏压的耗尽区完全分隔开。
随着漏极电压增加,漏极电流的大小变化如图:

图中的位置P即称为夹断点,在此点有一个很大的漏极电流称为饱和电流 I D s a t I_{Dsat} IDsat
当 V D V_D VD进一步上升后,会进入饱和区。此时 V D V_D VD继续增大, I D I_D ID也会保持不变。
随着漏极电压增加至饱和区,漏极电流的大小变化如图:

当漏极电压大于 V D s a t 时,电流基本上维持在 I D s a t 且与 V_{Dsat}时,电流基本上维持在I_{Dsat}且与 VDsat时,电流基本上维持在IDsat且与V_D$无关。
V G < 0 V_G<0 VG<0时漏极电压与漏极电流的关系
先定性地描述:当加入反向栅极偏压时,耗尽区宽度W随之增加。对较小的 V D V_D VD而言沟道就像是电阻器一般,但是具有较高的阻值,这是因为沟道的截面积减小的关系。
然后再来定量地描述。当
V
G
<
0
V_G<0
VG<0时,耗尽区宽度W会增大。当V增加至某一特定值时,耗尽区将接触到半绝缘衬底,此时的饱和漏极电压为:
V
D
s
a
t
=
q
N
D
a
2
2
ε
s
−
V
b
i
−
V
G
V_{Dsat}=\frac{qN_Da^2}{2\varepsilon_s}-V_{bi}-V_G
VDsat=2εsqNDa2−Vbi−VG
由公式可以得出结论:当
V
G
<
0
V_G<0
VG<0时,
V
D
s
a
t
V_{Dsat}
VDsat会下降。
V
G
<
0
V_G<0
VG<0时漏极电压与漏极电流的关系图:

电流电压关系
在线性区状态下的电流电压关系
沟道电阻:
R
=
ρ
L
A
=
L
Q
μ
n
N
D
Z
(
a
−
W
)
R=\rho \frac{L}{A}=\frac{L}{Q\mu_nN_DZ(a-W)}
R=ρAL=QμnNDZ(a−W)L
由欧姆定律可以得到:
d
V
=
I
D
R
=
I
D
d
y
Q
μ
n
N
D
Z
[
a
−
W
(
y
)
]
dV=I_DR=\frac{I_Ddy}{Q\mu_nN_DZ[a-W(y)]}
dV=IDR=QμnNDZ[a−W(y)]IDdy。对y做积分时的积分上限就是L。
由于
I
D
I_D
ID为定值,将上式进行换算得到:
I
D
d
y
=
q
μ
n
N
D
Z
[
a
−
W
(
y
)
]
d
V
I_Ddy=q\mu_nN_DZ[a-W(y)]dV
IDdy=qμnNDZ[a−W(y)]dV
与源极相距y处的耗尽区宽度为:
W
(
y
)
=
2
ε
s
[
V
(
y
)
+
V
G
+
V
b
i
]
q
N
D
W(y)=\sqrt{\frac{2\varepsilon_s[V(y)+V_G+V_{bi}]}{qN_D}}
W(y)=qND2εs[V(y)+VG+Vbi]
将W(y)代入可以:
d
V
=
q
N
D
ε
s
W
d
W
dV=\frac{qN_D}{\varepsilon_s}WdW
dV=εsqNDWdW
由于
I
D
d
y
=
q
μ
n
N
D
Z
[
a
−
W
(
y
)
]
d
V
I_Ddy=q\mu_nN_DZ[a-W(y)]dV
IDdy=qμnNDZ[a−W(y)]dV且对y做积分时的积分结果就是L,因此得到关断点P处的电流:
I
D
=
Z
μ
n
q
2
N
D
2
2
ε
s
L
[
a
(
W
2
2
−
W
1
2
)
−
2
3
(
W
2
3
−
W
1
3
)
]
I_D=\frac{Z\mu_nq^2N_D^2}{2\varepsilon_sL}[a(W_2^2-W_1^2)-\frac{2}{3}(W_2^3-W_1^3)]
ID=2εsLZμnq2ND2[a(W22−W12)−32(W23−W13)]
其中W1,W2如图所示:

将这两个宽度带入关于各种电压的表达式,可以得到关断点P处的电流:
I
=
I
P
[
V
D
V
P
−
2
3
(
V
D
+
V
G
+
V
b
i
V
p
)
3
/
2
+
2
3
(
V
G
+
V
b
i
V
p
)
3
/
2
]
I=I_P[\frac{V_D}{V_P}-\frac{2}{3}(\frac{V_D+V_G+V_{bi}}{V_p})^{3/2}+\frac{2}{3}(\frac{V_G+V_{bi}}{V_p})^{3/2}]
I=IP[VPVD−32(VpVD+VG+Vbi)3/2+32(VpVG+Vbi)3/2]
其中
I
P
=
Z
μ
n
q
2
N
D
2
a
3
2
ε
s
L
I_P=\frac{Z\mu_nq^2N_D^2a^3}{2\varepsilon_sL}
IP=2εsLZμnq2ND2a3
关断电压为:
V
p
=
q
N
D
a
2
2
ε
s
V_p=\frac{qN_Da^2}{2\varepsilon_s}
Vp=2εsqNDa2。这个关断电压即W2=a时的夹断电压
V
p
=
V
D
+
V
G
+
V
b
i
V_p=V_D+V_G+V_{bi}
Vp=VD+VG+Vbi
将关断点P处的电流进行泰勒展开得到:
I
D
≈
I
p
V
p
[
1
−
(
V
G
+
V
b
i
V
p
)
1
2
]
V
D
I_D \approx \frac{I_p}{V_p}[1-(\frac{V_G+V_{bi}}{V_p})^{\frac{1}{2}}]V_D
ID≈VpIp[1−(VpVG+Vbi)21]VD
将上式求导,可以得到跨导:
g
m
=
∂
I
D
∂
V
G
∣
V
D
固定
=
I
p
2
V
p
2
V
p
V
G
+
V
b
i
⋅
V
D
g_m=\frac{\partial I_D}{\partial V_G}|_{V_D固定}=\frac{I_p}{2V_p^2}\sqrt{\frac{V_p}{V_G+V_{bi}}} \cdot V_D
gm=∂VG∂ID∣VD固定=2Vp2IpVG+VbiVp⋅VD
本节总结
当电压超过 V D s a t V_{Dsat} VDsat时,电流被看作是一定值。注意电流-电压特性中有着三个不同的区域。当 V D V_D VD比较小时,沟道的截面积基本上与 V D V_D VD无关,此I-V特性为欧姆性质或是线性关系。于是将这个工作原理区域视为线性区。
当 V D ≥ V D s a t 时,电流于 V_D≥V_{Dsat}时,电流于 VD≥VDsat时,电流于I_{Dsat}$达到饱和,将这个工作原理区域称为饱和区。
当漏极电压进一步增加,栅极-沟道间二极管的雪崩击穿开始发生这使得漏极电流突然增加,这就是击穿区。
MESFET的电流-电压特性(比MOSFET多一个区“截止区”。
其中
V
D
s
a
t
V_{Dsat}
VDsat的表达式为:
V
D
s
a
t
=
q
N
D
a
2
2
ε
s
−
V
b
i
−
V
G
V_{Dsat}=\frac{qN_Da^2}{2\varepsilon_s}-V_{bi}-V_G
VDsat=2εsqNDa2−Vbi−VG
夹断电压
V
p
V_p
Vp为
I
p
=
Z
μ
n
q
2
N
D
2
a
3
2
ε
s
L
I_p=\frac{Z\mu_nq^2N_D^2a^3}{2\varepsilon_sL}
Ip=2εsLZμnq2ND2a3:;夹断电流
I
p
I_p
Ip为:
V
p
=
q
N
D
a
2
2
ε
s
V_p=\frac{qN_Da^2}{2\varepsilon_s}
Vp=2εsqNDa2。
电压Vp称为夹断电压,也就是当W=a时的总电压之和 ( V D + V G + V b i ) (V_D+V_G+V_{bi}) (VD+VG+Vbi)。
V
p
=
3.2
V
V_p=3.2V
Vp=3.2V的MESFET规一化的理想电流一电压特性:

MESFET的另一个重要参数是跨导。跨导:表示了在某个特定漏极电压下,相对于栅极电压的变化所造成漏极电流的变化。
在线性区,其
V
D
<
=
V
G
V_D<=V_G
VD<=VG,其漏极电流的可以表示为:
I
=
I
P
[
V
D
V
P
−
2
3
(
V
D
+
V
G
+
V
b
i
V
P
)
3
/
2
)
+
2
3
(
V
G
+
V
b
i
V
P
)
3
/
2
]
I=I_P[\frac{V_D}{V_P}-\frac{2}{3}(\frac{V_D+V_G+V_{bi}}{V_P})^{3/2})+\frac{2}{3}(\frac{V_G+V_{bi}}{V_P})^{3/2}]
I=IP[VPVD−32(VPVD+VG+Vbi)3/2)+32(VPVG+Vbi)3/2]。该式展开得到
I
D
≈
I
P
V
P
[
1
−
(
V
G
+
V
b
i
V
P
)
1
2
]
V
D
I_D\approx \frac{I_P}{V_P}[1-(\frac{V_G+V_{bi}}{V_P})^{\frac{1}{2}}]V_D
ID≈VPIP[1−(VPVG+Vbi)21]VD
再由跨导的定义,我们可以定量得出跨导的计算式:
g
m
=
∂
I
D
∂
V
G
∣
V
D
固定
=
I
p
2
V
p
2
V
p
V
G
+
V
b
i
⋅
V
D
g_m={\partial I_D}{\partial V_G}|_{V_D固定}=\frac{I_p}{2V_p^2}\sqrt{\frac{V_p}{V_G+V_{bi}}} \cdot V_D
gm=∂ID∂VG∣VD固定=2Vp2IpVG+VbiVp⋅VD
在饱和区状态下的电流电压关系
饱和漏极电流为:
I
D
s
a
t
=
I
p
[
1
3
−
V
G
+
V
b
i
V
p
+
2
3
(
V
G
+
V
b
i
V
p
)
3
/
2
]
I_{Dsat}=I_p[\frac{1}{3}-\frac{V_G+V_{bi}}{V_p}+\frac{2}{3}(\frac{V_G+V_{bi}}{V_p})^{3/2}]
IDsat=Ip[31−VpVG+Vbi+32(VpVG+Vbi)3/2]
此时的饱和漏极电压为:
V
D
s
a
t
=
V
p
−
V
G
−
V
b
i
V_{Dsat}=V_p-V_G-V_{bi}
VDsat=Vp−VG−Vbi
跨导为:
g
m
=
I
p
V
p
(
1
−
V
G
+
V
b
i
V
p
)
g_m=\frac{I_p}{V_p} (1-\sqrt{\frac{V_G+V_{bi}}{V_p}})
gm=VpIp(1−VpVG+Vbi)
带入
I
p
,
V
p
I_p,V_p
Ip,Vp后可以得到:
g
m
=
Z
μ
n
q
N
D
a
L
(
1
−
V
G
+
V
b
i
V
p
)
g_m=\frac{Z\mu_nqN_Da}{L}(1-\sqrt{\frac{V_G+V_{bi}}{V_p}})
gm=LZμnqNDa(1−VpVG+Vbi)
如果饱和区的 V D V_D VD继续上升,则会发生击穿。我们定义击穿电压为: V B = V D + V G V_B=V_D+V_G VB=VD+VG
该小节习题见例4。
增强型MESFET的电压电流特性
与MOSFET相似地,我们定义一个阈值电压
V
T
V_T
VT。
已知
V
p
=
V
b
i
+
V
T
V_p=V_{bi}+V_T
Vp=Vbi+VT,且
I
D
s
a
t
=
I
p
[
1
3
−
V
G
+
V
b
i
V
p
+
2
3
(
V
G
+
V
b
i
V
p
)
3
/
2
]
I_{Dsat}=I_p[\frac{1}{3}-\frac{V_G+V_{bi}}{V_p}+\frac{2}{3}(\frac{V_G+V_{bi}}{V_p})^{3/2}]
IDsat=Ip[31−VpVG+Vbi+32(VpVG+Vbi)3/2],对上式进行泰勒展开得到:
I
D
s
a
t
≈
Z
μ
n
ε
s
2
a
L
(
V
G
−
V
L
)
2
I_{Dsat} \approx \frac{Z\mu_n \varepsilon_s}{2aL}(V_G-V_L)^2
IDsat≈2aLZμnεs(VG−VL)2
对
I
D
s
a
t
I_{Dsat}
IDsat求导可以得到增强型MESFET的跨导:
g
m
=
d
I
D
s
a
t
d
V
G
=
Z
μ
n
ε
s
a
L
(
V
G
−
V
L
)
g_m=\frac{dI_{Dsat}}{dV_G}=\frac{Z\mu_n \varepsilon_s}{aL} (V_G-V_L)
gm=dVGdIDsat=aLZμnεs(VG−VL)
耗尽型与增强型MESFET的对比图:

电流电压特性(与频率特性)
MESFET无法再将输入信号放大时的频率,称为截止频率: f T = g m 2 π C G < I p / V p 2 π Z L ( ε s / W ‾ ) ≈ μ n q N D a 2 2 π ε s L 2 f_T=\frac{g_m}{2\pi C_G}<\frac{I_p/V_p}{2\pi ZL}(\varepsilon_s/\overline{W}) \approx \frac{\mu_nqN_Da^2}{2\pi \varepsilon_sL^2} fT=2πCGgm<2πZLIp/Vp(εs/W)≈2πεsL2μnqNDa2
截止频率对于晶体管,是越大越好的。因此由截止频率的表达式,我们可以得到诸多高频性能的改进方案。比如:1.使用具有较高载流子迁移率与较短沟道长度的MESFET。
在大电场下,截止频率使用新的关于饱和速度的表达式:KaTeX parse error: Undefined control sequence: \piL at position 17: …_T=\frac{v_s}{2\̲p̲i̲L̲}。此时改变高频性能的改进方案有:1.缩小栅极长度 2.使用高速度的半导体。
综上所述,高MESFET高频性能的改进方案有:1.使用具有较高载流子迁移率与较短沟道长度的MESFET;2.缩小栅极长度;3.使用高速度的半导体。

调制掺杂场效应晶体管
调制掺杂场效应晶体管为异质结构的场效应器件,又称为高电子迁移率品体管、二维电子气场效应品体管以及选择性掺杂异质结构品体管。通常通称为异质结场效应晶体管。
传统MODFET的透视图如下,其特征是栅极下方的异质结结构以及调制掺杂层:
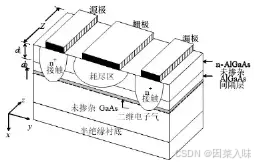
SiGe MODFET可以利用现有的硅晶片厂去制作,特点是具有高电子迁移率以及较高的平均速度和峰值速度。
课后习题
例1:求出如图所示钨-硅二极管的施主浓度与势垒高度。
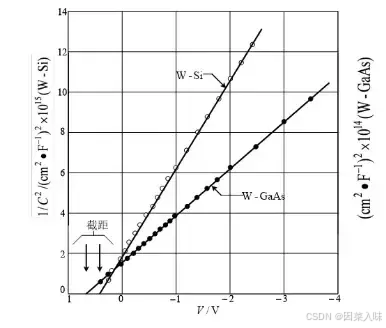
所需要用到的公式1.斜率
d
(
1
C
2
)
d
V
=
2
q
ε
s
N
D
\frac{d(\frac{1}{C^2})}{dV}=\frac{2}{q\varepsilon_sN_D}
dVd(C21)=qεsND2可以得到用于掺杂的施主杂质浓度为:
N
D
=
2
q
ε
s
⋅
−
1
d
(
1
C
2
/
d
V
)
N_D=\frac{2}{q\varepsilon_s}\cdot \frac{-1}{d(\frac{1}{C^2}/dV)}
ND=qεs2⋅d(C21/dV)−1 2.由截距等于
2
q
ε
s
N
D
V
b
i
\frac{2}{q\varepsilon_sN_D}V_{bi}
qεsND2Vbi可以得到
V
b
i
V_{bi}
Vbi。
最后由
V
b
i
=
ϕ
B
n
−
V
n
V_{bi}=\phi_{Bn}-V_n
Vbi=ϕBn−Vn和
V
n
=
E
C
−
E
F
q
=
k
T
q
l
n
N
C
N
D
V_n=\frac{E_C-E_F}{q}=\frac{kT}{q}ln\frac{N_C}{N_D}
Vn=qEC−EF=qkTlnNDNC,可以求得势垒高度
ϕ
B
n
\phi_{Bn}
ϕBn
例2:对
N
D
=
1
0
16
c
m
3
N_D=10^{16}cm^3
ND=1016cm3的钨-硅肖特基二极管而言,请由下图求出势垒高度与耗尽区宽度。假设硅中少数载流子的寿命为10^{-6}s,比较饱和电流
J
s
J_s
Js与
J
p
0
J_{p0}
Jp0
所需要用到的公式1.饱和电流密度
J
S
=
A
∗
T
2
e
x
p
(
−
q
ϕ
B
n
k
T
)
J_S=A^*T^2exp(-\frac{q\phi_{Bn}}{kT})
JS=A∗T2exp(−kTqϕBn) 2.势垒高度
ϕ
B
n
=
E
C
−
E
F
\phi_{Bn}=E_C-E_F
ϕBn=EC−EF,而
E
C
−
E
F
E_C-E_F
EC−EF可以用杂质浓度与本征载流子浓度表示,
E
C
−
E
F
=
k
T
q
l
n
(
N
A
N
D
n
i
2
)
E_C-E_F=\frac{kT}{q}ln(\frac{N_AN_D}{n_i^2})
EC−EF=qkTln(ni2NAND) 3.内建电势与势垒电势的关系式
ϕ
B
n
=
V
n
+
V
b
i
\phi_{Bn}=V_n+V_{bi}
ϕBn=Vn+Vbi 4.热平衡时的耗尽区宽度表达式
W
=
2
ε
s
V
b
i
q
N
D
W=\sqrt{\frac{2\varepsilon_sV_{bi}}{qN_D}}
W=qND2εsVbi 5.扩散长度
L
p
=
D
p
τ
p
L_p=\sqrt{D_p\tau_p}
Lp=Dpτp 6.热平衡时从金属流向半导体的电流密度
J
p
0
=
q
D
p
n
i
2
L
p
N
D
J_{p0}=\frac{qD_pn_i^2}{L_pN_D}
Jp0=LpNDqDpni2。
例4:当T=300K时,一个以金作接触的n沟道砷化镓MESFET。假设势垒高度为0.89V。若n沟道浓度为2x1015cm3,且沟道厚度为0.6um。计算夹断电压以及内建电势。已知确化镓的介电常数为12.4。
所需要用到的公式1.关断电压计算式:
V
p
=
q
N
D
a
2
2
ε
s
V_p=\frac{qN_Da^2}{2\varepsilon_s}
Vp=2εsqNDa2 2.导带底与费米能级之差:
V
n
q
=
E
c
−
E
F
=
k
T
⋅
l
n
(
N
c
N
D
)
V_nq=E_c-E_F=kT\cdot ln(\frac{N_c}{N_D})
Vnq=Ec−EF=kT⋅ln(NDNc) 3.势垒高度与内建电势的关系为:
V
b
i
=
q
ϕ
B
n
−
V
n
=
ψ
n
−
ψ
p
=
k
T
q
l
n
N
A
N
D
n
i
2
V_{bi}=q\phi_{Bn}-V_n=\psi_n-\psi_p=\frac{kT}{q}ln\frac{N_AN_D}{n_i^2}
Vbi=qϕBn−Vn=ψn−ψp=qkTlnni2NAND
