一：图像几何变化基础

（1）齐次坐标表示法

齐次坐标表示法：用$n+1$维向量表示$n$维向量的方法称为齐次坐标表示法。在齐次坐标中，原图像用点集$[x,y,1{]}^T$表示。使用齐次坐标表示法可以方便地进行矩阵运算，例如平移、旋转、缩放等变换操作。同时，它也可以简化透视投影等复杂操作的计算。在计算机图形学和计算机视觉等领域中，齐次坐标表示法已经成为了一种标准的表示方法，被广泛应用于三维图形建模、计算机动画、计算机视觉、机器人学等领域

举例：

假设有一个三维坐标系中的点$P$，其坐标为$(x,y,z)$，如果使用齐次坐标表示法，可以将其表示为$[x,y,z,1]$。接下来，假设我们想要对点$P$进行平移变换，将其沿着 $x$ 轴方向平移10个单位，沿着 $y$ 轴方向平移5个单位，沿着 $z$ 轴方向平移2个单位。如果使用传统的三维坐标表示方法，需要对每个坐标分别进行加减操作

x' = x + 10
y' = y + 5
z' = z + 2

但是，如果使用齐次坐标表示法，则可以使用矩阵运算进行平移变换

T = [1, 0, 0, 10] 
	[0, 1, 0, 5] 
	[0, 0, 1, 2] 
	[0, 0, 0, 1] 
P' = T * P

其中，T 是一个4x4的矩阵，用于表示平移变换。P’ 是平移后的点的齐次坐标表示

（2）图像的几何变换

图像的几何变换：通过齐次坐标中，原图像进行平移、缩放、旋转等几何变换，可以用一个变换矩阵$T$表示

如下矩阵$T$，其中

• $a$,$b$,$c$,$d$用于图形的比例、对称、错切、旋转等基本变换
• $k$,$m$用于图形的平移变换
• $p,q$用于投影变换
• $s$用于全比例变换

$$\mathbf{T}=\left[\begin{array}{lll}\mathbf{a}& \mathbf{b}& \mathbf{k}\\ \mathbf{c}& \mathbf{d}& \mathbf{m}\\ \mathbf{p}& \mathbf{q}& \mathbf{s}\end{array}\right]$$

实现2D图像几何变换的基本变换的一般过程是

$$变换矩阵T\times 变换前的点集矩阵=变换后的点集矩阵$$

（3）图像插值运算

A：概述

图像插值运算：利用已知邻近像素点的灰度值来产生未知像素点的灰度值。包括

• 最近邻插值： 非整数像素灰度值就等于距离最近的像素的灰度值
• 双线性插值： 利用非整数像素点周围的四个像素点的相关性，通过双线性算法计算得出的
• 双三次插值： 利用非整数像素点周围的16个像素点进行计算

B：双线性插值

要想了解双线性插值就必须先要知道什么是线性插值。简单来说，线性插值就是有两个点$A$、$B$，要在$AB$中间插入一个点$C$（点$C$坐标在$AB$连线上），就直接让$C$的值落在$AB$的值的连线上就可以了

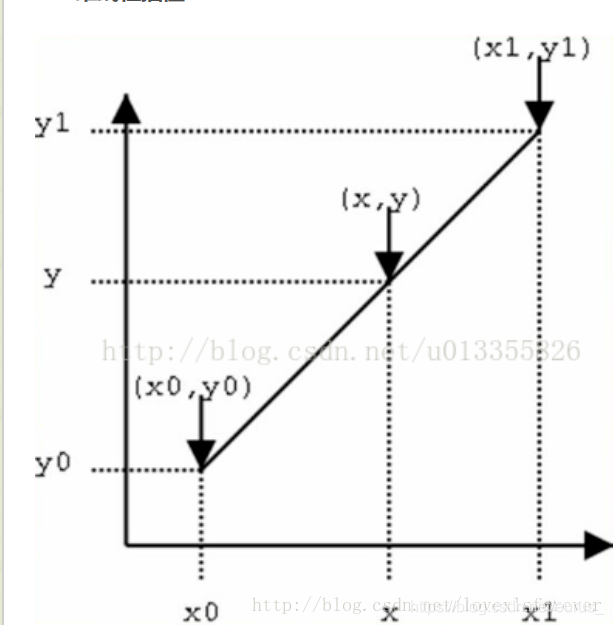
如下，线性插值本质就是用$x$和$x_0,x_1$的距离作为一个权重，用于$y_0$和$y_1$的加权

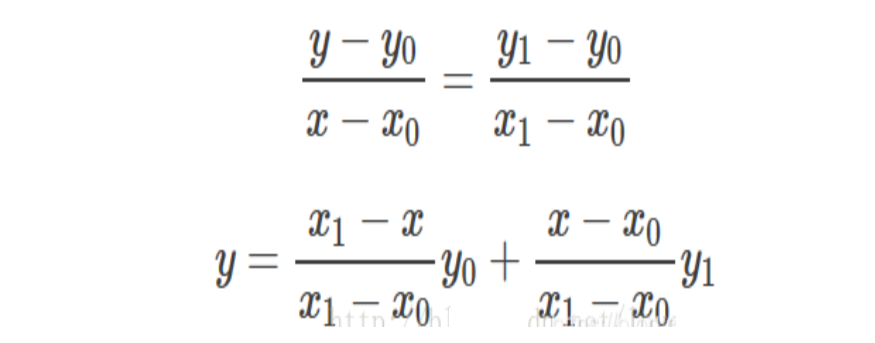
双线性插值运算本质就是在两个方向上做线性插值。如下图，我们需要求$P$点的像素值。已知了$Q_{11},Q_{21},Q_{12},Q_{22}$的坐标。也知道$Q_{11},Q_{21},Q_{12},Q_{22}$的像素值

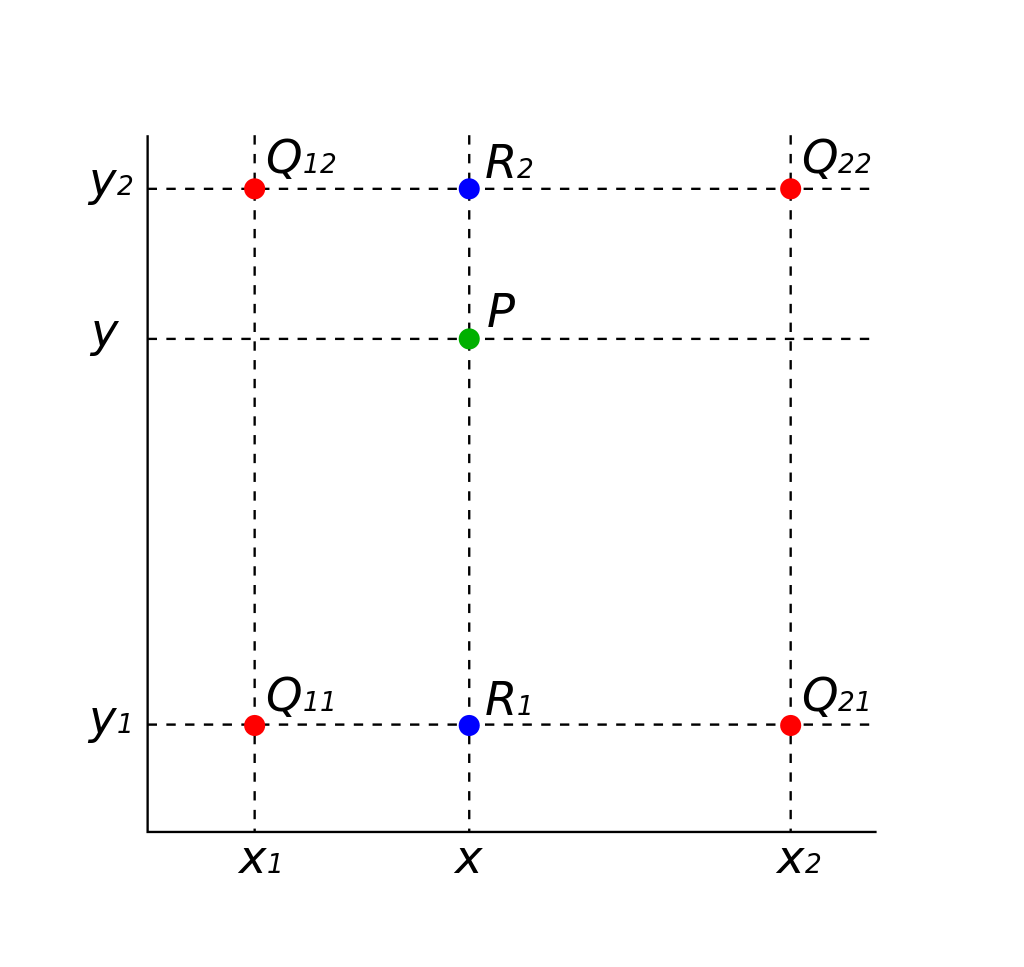
所以先用关于$x$的单线性插值去分别计算$R_1,R_2$的像素值

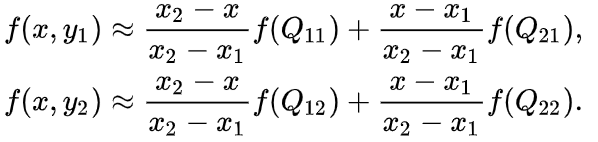
再使用关于$y$方向的单线性插值计算$P$点的像素值

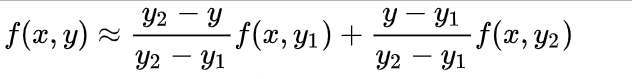
（4）图像几何变换：后向映射法

后向映射法：

• 根据不同的几何变换公式计算新图像的尺寸
• 根据几何变换的逆变换，对新图像中的每一点确定其在原图像中的对应点
• 按对应关系给新图像中各个像素赋值
  • 若新图像中像素点在原图像中的对应点坐标存在则直接赋值
  • 若新图像中像素点在原图像中的对应点坐标超出图像宽高范围则直接赋背景色
  • 若新图像中像素点在原图像中的对应点坐标在图像宽高范围内则采用插值的方法计算

二：图像的位置变换

图像的位置变换：图像的位置变换是指图像的大小和形状不发生变化，只是图像像素点的位置发生变化，图像的位置变换主要是用于目标识别中的目标配准。包括

• 平移
• 镜像
• 旋转

（1）平移

A：概述

原理：变换公式如下

$$\{\begin{array}{l}{x}^{\prime }=x+\Delta x\\ y^{\prime }=y+\Delta y\end{array}$$

矩阵表示如下

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}1& 0& \Delta x\\ 0& 1& \Delta y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{l}x\\ y\\ 1\end{array}\right]$$

如果平移后不丢失信息则需要扩大画布

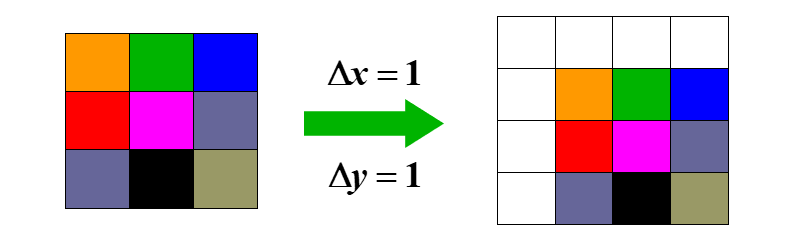
B：程序

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册

• T = maketform(TRANSFORMTYPE,...)
• B = imtransform(A,TFORM,INTERP,PARAM1,VAL1,PARAM2,VAL2,...)

maketform函数：在MATLAB中，maketform函数是一个用于创建仿射变换矩阵的函数，它可以将任意的仿射变换表示为一个3x3的矩阵。maketform函数的参数如下

• 第一个参数tformtype指定了变换的类型，可以是以下几种
  • nonreflective similarity：非反射相似变换
  • affine：仿射变换
  • projective：投影变换
• 第二个参数inpoints和第三个参数outpoints是输入图像和输出图像上的点坐标，它们描述了变换前后各个点的对应关系。这里要求这两个参数都是n×2的矩阵，每一行表示一个点的坐标。
• 第四个参数normalize指定是否对输入和输出点进行归一化。如果设置为true，则maketform函数会将输入和输出点缩放到[-1, 1]范围内，使得仿射变换矩阵的求解更加稳定。
• 第五个参数params是可选的，它只有在tformtype为projective时才需要指定。它是一个3x3的矩阵，描述了一个额外的投影变换，它会被添加到仿射变换矩阵中

imtransform函数：该函数可以对图像进行平移、旋转、缩放等变换操作。该函数的参数如下

• 第一个参数A是要进行变换的原始图像
• 第二个参数TFORM是一个仿射变换矩阵，它描述了要执行的变换类型和参数
• 第三个参数INTERP表示插值方法的字符串或函数句柄。在进行图像变换时，原图像的像素会被映射到目标图像的新位置，但是像素点之间的间隔可能会不同。为了填充这些间隔，需要使用插值方法计算新像素点的像素值。常用的插值方法有双线性插值、双立方插值、最近邻插值等。可以使用 interp2 函数来查看不同插值方法的效果
• PARAM1、VAL1、PARAM2、VAL2 等：表示一些可选参数的名称和对应的值。不同的变换类型和插值方法可能需要不同的参数。例如，在使用双立方插值时，可以使用 bicubic 选项来控制插值的平滑度。可以使用 imwarp 函数查看不同选项的效果

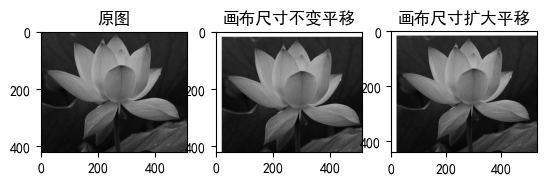
实现如下效果

代码含义：

• 首先，使用 imread 函数读取名为 “lotus.jpg” 的图像，并将其存储在变量 Image 中
• 然后，定义平移量 deltax 和 deltay 分别为 20。这表示图像将沿着 x 轴和 y 轴方向移动 20 个像素
• 接着，使用 maketform 函数创建一个仿射变换类型的结构体 T，其中 [1 0 0;0 1 0;deltax deltay 1] 表示一个平移变换矩阵。这个变换矩阵将图像沿着 x 轴和 y 轴方向移动 deltax 和 deltay 个像素
• 然后，使用 imtransform 函数对图像进行平移变换，并生成两个新的图像。第一个新图像 NewImage1 是在不改变图像大小的情况下进行平移的结果。第二个新图像 NewImage2 则是在将图像大小扩大后进行平移的结果
  • [1 size(Image,2)] 是一个包含两个元素的行向量，用于设置 imtransform 函数的 'XData' 选项。其中
    • 第一个元素 1 表示新图像的左侧边界的 x 坐标，即 x 轴方向上的最小值。
    • 第二个元素 size(Image,2) 表示新图像的右侧边界的 x 坐标，即 x 轴方向上的最大值
  • 因此，[1 size(Image,2)] 表示新图像在 x 轴方向上的尺寸，其宽度等于原始图像 Image 在 x 轴方向上的宽度。这个尺寸将用于限制变换后的图像的大小，使得图像不会被裁剪或变形.类似地，'YData' 选项中的 [1,size(Image,1)] 表示新图像在 y 轴方向上的尺寸，其高度等于原始图像 Image 在 y 轴方向上的高度
• 最后，使用 subplot 和 imshow 函数将原图和两个新图像展示在同一幅图中，并设置标题。其中 XData 和 YData 选项是用于设置新图像的尺寸的，FillValue 选项是用于设置新像素点的填充值

Image=imread('lotus.jpg');
deltax=20;deltay=20;
T=maketform('affine',[1 0 0;0 1 0;deltax deltay 1]);
NewImage1=imtransform(Image,T,'XData',[1 size(Image,2)],'YData',[1,size(Image,1)],'FillValue',255);
NewImage2=imtransform(Image,T,'XData',[1 size(Image,2)+deltax],'YData',[1,size(Image,1)+deltay],'FillValue',255);
subplot(131),imshow(Image),title('原图');
subplot(132),imshow(NewImage1),title('画布尺寸不变平移');
subplot(133),imshow(NewImage2),title('画布尺寸扩大平移');

Python实现：使用Python实现上述同样的功能

• 我们首先使用 OpenCV 的 imread 函数读取名为 “lotus.jpg” 的图像，并将其存储在变量 Image 中。然后，我们定义平移量 deltax 和 deltay 分别为 20
• 接着，我们使用 np.float32 函数创建一个仿射变换矩阵 T，其中 [[1, 0, deltax], [0, 1, deltay]] 表示一个平移变换矩阵。这个变换矩阵将图像沿着 x 轴和 y 轴方向移动 deltax 和 deltay 个像素
• 然后，我们使用 cv2.warpAffine 函数对图像进行平移变换，并生成两个新的图像。第一个新图像 NewImage1 是在不改变图像大小的情况下进行平移的结果。第二个新图像 NewImage2 则是在将图像大小扩大后进行平移的结果
• 最后，我们使用 Matplotlib 的 plt.subplot 和 plt.imshow 函数将原图和两个新图像展示在同一幅图中，并设置标题。其中 borderValue 参数是用于设置新像素点的填充值。注意在展示图像前，需要使用 cv2.cvtColor 函数将 BGR 格式的图像转换为 RGB 格式的图像，以便于在 Matplotlib 中正确显示颜色

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

# 读取图像
Image = cv2.imread('lotus.jpg')

# 定义平移量
deltax, deltay = 20, 20

# 创建仿射变换矩阵
T = np.float32([[1, 0, deltax], [0, 1, deltay]])

# 对图像进行仿射变换
NewImage1 = cv2.warpAffine(Image, T, (Image.shape[1], Image.shape[0]), borderValue=(255, 255, 255))
NewImage2 = cv2.warpAffine(Image, T, (Image.shape[1]+deltax, Image.shape[0]+deltay), borderValue=(255, 255, 255))

# 展示图像
plt.subplot(1, 3, 1), plt.imshow(cv2.cvtColor(Image, cv2.COLOR_BGR2RGB)), plt.title('原图')
plt.subplot(1, 3, 2), plt.imshow(cv2.cvtColor(NewImage1, cv2.COLOR_BGR2RGB)), plt.title('画布尺寸不变平移')
plt.subplot(1, 3, 3), plt.imshow(cv2.cvtColor(NewImage2, cv2.COLOR_BGR2RGB)), plt.title('画布尺寸扩大平移')
plt.show()

（2）镜像

A：概述

原理：如下下依次为水平镜像、垂直镜像和对角镜像

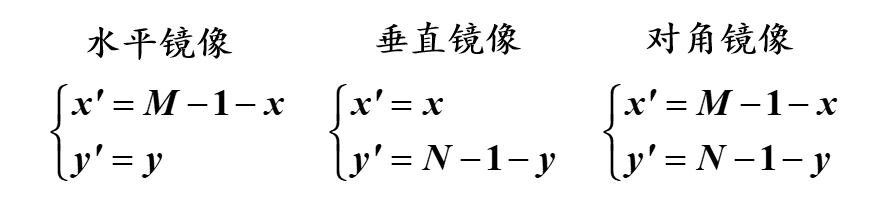
变换矩阵为

图像解释如下

B：程序

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册

• fliplr(X)：左右翻转
• flipud(X)：垂直翻转
• flipdim(X,DIM)：指定维度翻转
• rot(90)：旋转90°

flipdim(X)函数：用于将矩阵 X 按指定的维度 DIM 反转。参数 X 是需要反转的矩阵，参数 DIM 是一个整数，表示需要反转的维度。当 DIM 的值为 1 时，相当于调用 flipud(X)；当 DIM 的值为 2 时，相当于调用 fliplr(X)
实现对角镜像：先水平翻转再垂直翻转

实现如下效果

Image = imread('lotus.jpg')
HImage = flipdim(Image,2); % 水平
VImage = flipdim(Image,1); % 垂直
CImage = flipdim(HImage,1); % 对角
subplot(221),imshow(Image), title('原图');
subplot(222),imshow(HImage), title('水平翻转');
subplot(223),imshow(VImage), title('垂直翻转');
subplot(224),imshow(CImage), title('对角翻转');

Python实现：使用Python实现上述同样的功能

• cv2.flip(src, flipCode[, dst])：函数是OpenCV中用于翻转图像的函数，它可以对图像进行水平翻转、垂直翻转或同时进行水平和垂直翻转
  • src：待翻转的输入图像，可以是多通道图像
  • flipCode：指定翻转方式
    • 0：沿x轴（水平轴）翻转
    • 1：沿y轴（垂直轴）翻转
    • -1：同时沿x轴和y轴翻转
  • dst：可选，表示输出翻转后的图像。如果该参数为None，函数会自动创建一个大小和输入图像相同的输出图像。如果该参数不为None，它必须具有与输入图像相同的大小和数据类型

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

# 读取图像
Image = cv2.imread('lotus.jpg')

# 水平翻转
HImage = cv2.flip(Image, 1)
# 垂直翻转
VImage = cv2.flip(Image, 0)
# 对角翻转
CImage = cv2.flip(HImage, 0)

# 显示图像
plt.subplot(221),plt.imshow(cv2.cvtColor(Image, cv2.COLOR_BGR2RGB)),plt.title('原图')
plt.subplot(222),plt.imshow(cv2.cvtColor(HImage, cv2.COLOR_BGR2RGB)),plt.title('水平翻转')
plt.subplot(223),plt.imshow(cv2.cvtColor(VImage, cv2.COLOR_BGR2RGB)),plt.title('垂直翻转')
plt.subplot(224),plt.imshow(cv2.cvtColor(CImage, cv2.COLOR_BGR2RGB)),plt.title('对角翻转')
plt.show()

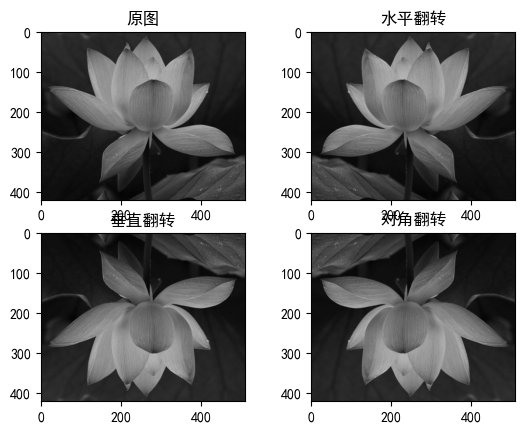
（3）旋转

A：概述

原理：变换公式如下

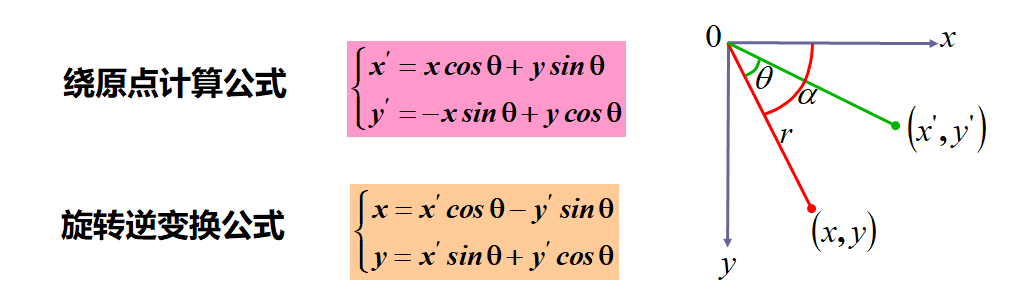
下图说明了具体的变换过程

**需要注意的是，在运算过程中，原图中的对应点超出图像范围，新图像中的点在原图像中没有对应点，直接赋背景色255（或赋0）；对于未超出图像范围但不是整数像素的对应点按最邻近插值，当然为提高效果，可采用双线性插值 **

B：程序

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册

• B = imrotate(A,ANGLE,METHOD,BBOX)

imrotate函数：用于对图像进行旋转操作

• A: 需要进行旋转操作的原始图像
• ANGLE: 旋转的角度，可以是正数或负数。当角度为正数时，表示顺时针方向旋转；当角度为负数时，表示逆时针方向旋转。单位为度（degree）
• METHOD: 旋转操作使用的插值方法。可以是以下字符串之一：
  • 'nearest'：最近邻插值法。该方法使用最近的像素值来进行插值计算，速度最快但是可能会导致图像出现锯齿。
  • 'bilinear'：双线性插值法。该方法使用相邻四个像素的加权平均值来进行插值计算，可以得到较为平滑的旋转结果。
  • 'bicubic'：双三次插值法。该方法使用相邻 16 个像素的加权平均值来进行插值计算，可以得到更加平滑的旋转结果，但是速度较慢。
• BBOX: 一个可选的布尔值，表示旋转后的图像是否应该被裁剪到包含所有像素的最小矩形区域。当为 true 时，表示进行裁剪；当为 false 时，表示不进行裁剪，默认为 true

实现如下效果

Image=im2double(imread('lotus.jpg'));
NewImage1=imrotate(Image,15);
NewImage2=imrotate(Image,15,'bilinear');
subplot(1,2,1),imshow(NewImage1);
subplot(1,2,2),imshow(NewImage2);
imwrite(NewImage1,'rotate11.jpg');
imwrite(NewImage2,'rotate12.jpg');

Python实现：使用Python实现上述同样的功能

• cv2.rotate()：
  • src：需要旋转的输入图像。
  • rotateCode：旋转方向的代码，可以是下列值之一：
    • cv2.ROTATE_90_CLOCKWISE：顺时针旋转90度。
    • cv2.ROTATE_180：旋转180度。
    • cv2.ROTATE_90_COUNTERCLOCKWISE：逆时针旋转90度。
  • dst：可选参数，输出图像。如果没有指定，则会在函数内部创建一个输出图像
• cv2.warpAffine()：用于将图像进行仿射变换
  • src: 输入图像。
  • M: 2x3的变换矩阵。矩阵中的前两列表示变换后的像素坐标x和y与变换前的像素坐标x和y之间的线性关系，第三列表示平移量。变换矩阵可以通过cv2.getAffineTransform()和cv2.getRotationMatrix2D()函数得到。
  • dsize: 输出图像大小。可以是一个元组，元组中的两个元素分别表示输出图像的宽度和高度。如果不指定该参数，则输出图像的大小与输入图像大小相同。
  • flags: 插值方法。包括cv2.INTER_NEAREST（最近邻插值）、cv2.INTER_LINEAR（双线性插值）、cv2.INTER_CUBIC（双三次插值）和cv2.INTER_LANCZOS4（Lanczos插值）。默认使用双线性插值。
  • borderMode: 边界填充方式。可以是cv2.BORDER_CONSTANT（常数填充）、cv2.BORDER_REPLICATE（复制边界像素）、cv2.BORDER_REFLECT（镜像填充）或cv2.BORDER_WRAP（环绕填充）。默认使用常数填充。
  • borderValue: 当borderMode为cv2.BORDER_CONSTANT时，指定边界填充的常数值。默认值为0

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 读取图像并转为浮点型
image = cv2.imread('lotus.jpg').astype(np.float32) / 255.0

# 旋转图像
new_image1 = cv2.rotate(image, cv2.ROTATE_15_CLOCKWISE)
new_image2 = cv2.warpAffine(image, cv2.getRotationMatrix2D((image.shape[1]/2, image.shape[0]/2), 15, 1), image.shape[:2], flags=cv2.INTER_LINEAR)

# 显示结果
plt.subplot(1, 2, 1)
plt.imshow(new_image1[..., ::-1])
plt.subplot(1, 2, 2)
plt.imshow(new_image2[..., ::-1])

# 保存结果
cv2.imwrite('rotate11.jpg', new_image1 * 255)
cv2.imwrite('rotate12.jpg', new_image2 * 255)

# 显示图像
plt.show()

三：图像的形状变换

（1）缩放

A：概述

原理：变换公式和矩阵表示如下

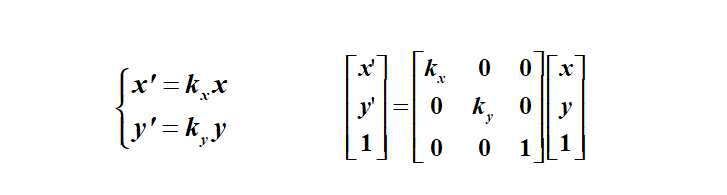
$M\times N$图像会缩放为：$k_{x}M\times k_{y}N$

下图以一实例说明了具体变换过程

B：程序

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册

• B=imresize(A,SCALE,METHOD))
• B=imresize(A,[NUMROWS NUMCOLS], METHOD))[Y, NEWMAP] = imresize(X, MAP, SCALE, METHOD))

imresize()函数：用于对图像进行缩放的函数

• A：待缩放图像
• SCANLE：缩放比例
• METHOD：缩放方法
  • nearest：最近邻插值法，即将缩放后的像素点的值设置为距离该点最近的原图像素点的值。
  • bilinear：双线性插值法，即在原图像素点的四个相邻点中加权平均得到缩放后像素点的值。
  • bicubic：双三次插值法，是对双线性插值法的一种改进，加入了更多的权重系数
• OutputSize：指定输出图像的大小，可以指定为一个数值，表示输出图像的宽度（高度按比例缩放），也可以指定为一个二元组（[M,N]），表示输出图像的宽度和高度。
• Antialiasing：指定是否开启抗锯齿功能，可以设置为true或false，默认为true

实现如下效果

Image=im2double(imread('lotus.jpg'));
NewImage1=imresize(Image,1.5,'nearest');
NewImage2=imresize(Image,1.5,'bilinear');
subplot(1,2,1),imshow(NewImage1), title('最近邻插值缩放');
subplot(1,2,2),imshow(NewImage2), title('双线性插值缩放');

Python实现：使用Python实现上述同样的功能

• cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]])：是OpenCV中用于调整图像大小的函数，其参数如下
  • src：是输入的图像，可以是任意维度的数组
  • dsize：是输出图像的大小，可以是一个元组，也可以是一个整数，表示输出图像的宽和高。如果dsize是一个整数，则输出图像的大小为(dsize, dsize)
  • dst：是可选的输出图像，如果指定了该参数，则输出图像将被写入到该数组中。如果没有指定该参数，则函数将创建一个输出图像数组
  • fx和fy参数是可选的缩放因子，表示将输入图像沿着X轴和Y轴分别缩放的比例。默认情况下，它们的值都为0，表示使用dsize参数指定的大小来进行缩放
  • interpolation参数是可选的插值方法，用于在缩放过程中计算输出图像中每个像素的值。它可以是以下任意一种
    • cv2.INTER_NEAREST - 最近邻插值
    • cv2.INTER_LINEAR - 双线性插值（默认）
    • cv2.INTER_AREA - 区域插值
    • cv2.INTER_CUBIC - 双三次插值
    • cv2.INTER_LANCZOS4 - Lanczos插值（具有更好的抗锯齿效果）

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

# 读取图像
image = cv2.imread('lotus.jpg')

# 最近邻插值缩放
new_image1 = cv2.resize(image, None, fx=1.5, fy=1.5, interpolation=cv2.INTER_NEAREST)

# 双线性插值缩放
new_image2 = cv2.resize(image, None, fx=1.5, fy=1.5, interpolation=cv2.INTER_LINEAR)

# 显示图像
plt.subplot(1, 2, 1)
plt.imshow(new_image1)
plt.title('最近邻插值缩放')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.imshow(new_image2)
plt.title('双线性插值缩放')
plt.axis('off')

plt.show()

（2）错切

A：概述

原理：平面景物在投影平面上的非垂直投影，使图像中的图形产生扭变

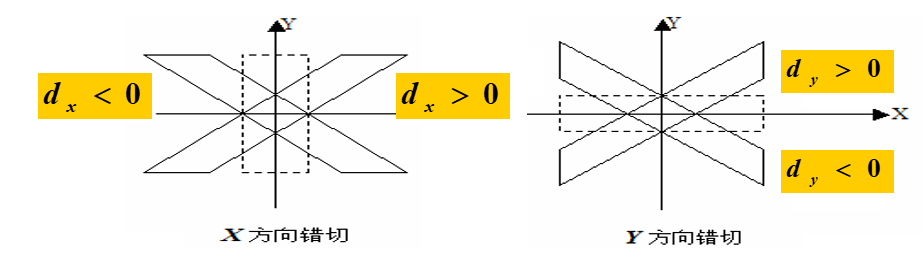
变换公式和矩阵表示如下

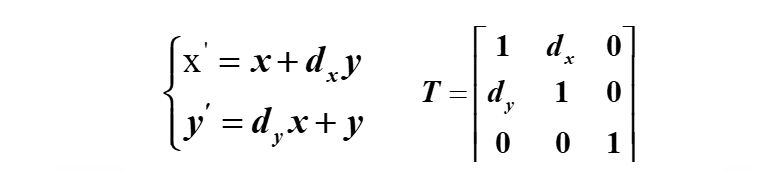
B：程序

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册（已在前文介绍）

• T = maketform(TRANSFORMTYPE,...)
• B = imtransform(A,TFORM,INTERP,PARAM1,VAL1,PARAM2,VAL2,...)

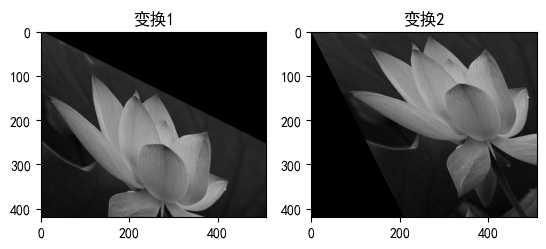
实现效果如下

Image=im2double(imread('lotus.jpg'));
tform1=maketform('affine',[1 0 0;0.5 1 0; 0 0 1]);
tform2=maketform('affine',[1 0.5 0;0 1 0; 0 0 1]);
NewImage1=imtransform(Image,tform1);
NewImage2=imtransform(Image,tform2);
subplot(1,2,1),imshow(NewImage1), title('变换1');
subplot(1,2,2),imshow(NewImage2), title('变换1');

Python实现：使用Python实现上述同样的功能

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

# 读取图像
image = cv2.imread('lotus.jpg')

# 定义仿射变换矩阵
tform1 = np.float32([[1, 0, 0], [0.5, 1, 0], [0, 0, 1]])
tform2 = np.float32([[1, 0.5, 0], [0, 1, 0], [0, 0, 1]])

# 进行仿射变换
new_image1 = cv2.warpAffine(image, tform1[:2, :], (image.shape[1], image.shape[0]))
new_image2 = cv2.warpAffine(image, tform2[:2, :], (image.shape[1], image.shape[0]))

# 显示结果
plt.subplot(1, 2, 1)
plt.imshow(new_image1)
plt.title('变换1')

plt.subplot(1, 2, 2)
plt.imshow(new_image2)
plt.title('变换2')

plt.show()