当前位置： 首页 > article >正文

详细手把手教会二叉树链式结构【数据结构】

article 2025/1/11 22:59:12

文章目录

    • 二叉树链式结构的实现
      • 前序遍历
      • 中序遍历
      • 后序遍历
      • 层序遍历
      • 树节点个数
      • 树的深度
      • 第K层节点个数
    • 查找二叉树中的元素

在这里插入图片描述

二叉树链式结构的实现

在这里插入图片描述

typedef int BinartTreeType;
typedef struct BinarytTreeNode
{
	BinartTreeType data;//节点存放的数据
	struct BinarytTreeNode* left; //指向当前节点的左孩子
	struct BinarytTreeNode* right;//指向当前节点的右孩子

}BTNode;

前序遍历

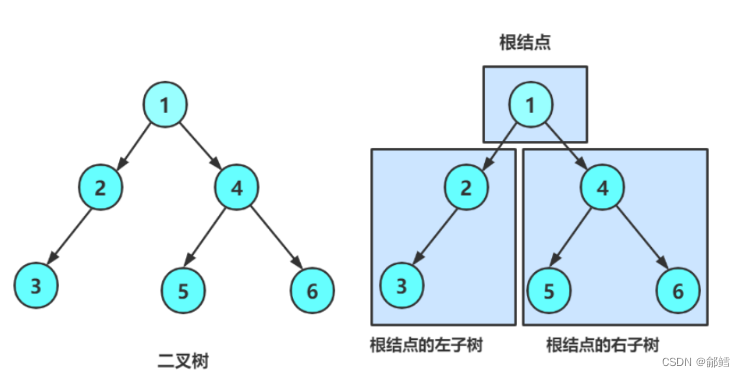
访问根结点的操作发生在遍历其左右子树之前
简单来说就是 根节点 左子树 右子树

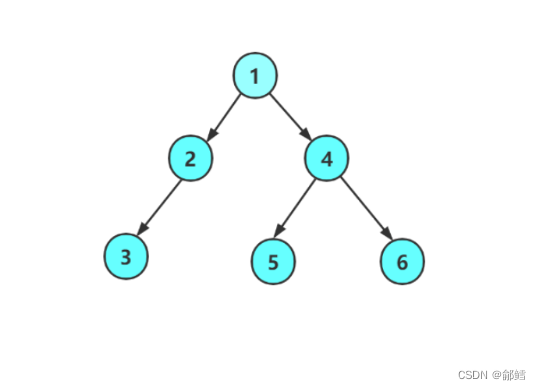
1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL

在这里插入图片描述

  BTNode* CreateTree()
  {
	  BTNode* node1 = BuyNode(1);
	  BTNode* node2 = BuyNode(2);
	  BTNode* node3 = BuyNode(3);
	  BTNode* node4 = BuyNode(4);
	  BTNode* node5 = BuyNode(5);
	  BTNode* node6 = BuyNode(6);
	  BTNode* node7 = BuyNode(7);

	  node1->left = node2;
	  node1->right = node4;
	  node2->left= node3;
	  node4->left = node5;
	  node4->right = node6;
	  //node3->right = node7;

	  return node1;
  }
  void PreOreder(BTNode* root) //根 左子树 右子树 
  {
	  if (root == NULL)
	  {
		  printf("NULL ");
		  return;
	  }
	  printf("%d ", root->data);
	  PreOreder(root->left);
	  PreOreder(root->right);
  }
  int main()
  {
	  BTNode* root = CreateTree();
	  PreOreder(root);
	  return 0;
  }

从根节点1开始遍历 , 遍历完1这个根节点 ,然后去遍历1这个根节点的左子树(2) ，遍历到节点2时 , 但是节点 2 又被分成根节点 (2)、左子树(3) 、右子树（NULL) 。遍历到节点3时 ，节点3又被分成根节点 (3)、左子树(NULL) 、右子树（NULL) ,对于节点3而言 ，3的左子树（NULL）走完 ，就走节点3的右子树（NULL) , 3这一整棵树作为2的左子树 ，2的左子树走完了 ，就走2的右子树（NULL) , 2的整棵树作为1的左子树, ,2这一整棵树走完了, 就走到1的右子树4 ，但是节点 4 又被分成根节点 (4)、左子树(5) 、右子树（6) ，然后走到4的左子树5 ，但是节点 5 又被分成根节点 (5)、左子树(NULL) 、右子树（NULL) ，5的整棵树作为4的左子树, ,5这一整棵树走完了,就来到了4的右子树（6），但是节点 6又被分成根节点 (6)、左子树(NULL) 、右子树（NULL)， 4的左子树，右子树都遍历完了 ,4的这一整棵树也遍历完了,4这一整棵树是作为1的右子树 ,

前序遍历就是将每一个节点不断拆分成 根，左子树 ，右子树的一个过程
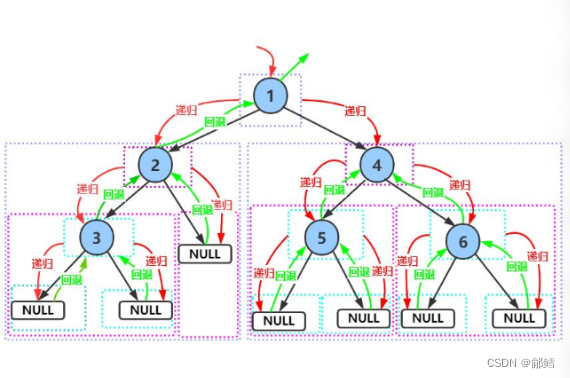
在这里插入图片描述

前序遍历递归展开图,以左子树为例，右子树并未画出

在这里插入图片描述

中序遍历

访问根结点的操作发生在遍历其左右子树之中（间）
简单来说就是 左子树 根节点 右子树

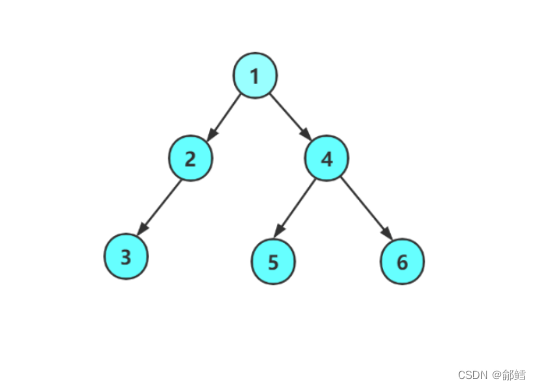
在这里插入图片描述

NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL

节点 1被分成根节点 (1)、左子树(2) 、右子树（4) ,先遍历1的左子树2，遇到节点2不能直接访问,得继续拆分 , 节点 2被分成根节点 (2)、左子树(3) 、右子树（NULL) ，遇到节点3，节点3又被分成根节点 (3)、左子树(NULL) 、右子树（NULL) ，那什么样的情况，能直接访问左子树？ 遇到空树就可以直接访问,因为空树不能再被拆分，是最小规模的子问题 。 所以第一个访问的是节点3的左子树(NULL) ,再到根节点（3） ，再到3的右子树(NULL) 。3的整棵树作为2的左子树, ,3这一整棵树走完了。2的左子树访问完了 ，就可以访问根节点2了 ，然后到2的右子树（NULL)，2的整棵树作为1的左子树, ,2这一整棵树走完了 ，就可以访问根节点1了 ，然后到1的右子树（4) ，遇到节点4不能直接访问,得继续拆分，节点 4 又被分成根节点 (4)、左子树(5) 、右子树（6)，遇到节点5不能直接访问,得继续拆分，节点 5 又被分成根节点 (5)、左子树(NULL) 、右子树（NULL) ，然后访问5的左子树（NULL) ,、5（根节点）、5的右子树（NULL），5这一整棵树走完了。4的左子树访问完了 ，就可以访问根节点4了 ，然后到4的右子树（6)，遇到节点6不能直接访问,得继续拆分，节点 6又被分成根节点 (6)、左子树(NULL) 、右子树（NULL) ，然后访问6的左子树（NULL) ,、6（根节点）、6的右子树（NULL），6这一整棵树走完了，4的右子树访问完了 ， 4这一整棵树作为1的右子树也访问完了

中序遍历访问的第一个一定是NULL ，因为任何一个节点都可以被视作根节点 ,有些书上中序遍历访问的第一个不是NULL ,是因为书上省略了

  BTNode* CreateTree()
  {
	  BTNode* node1 = BuyNode(1);
	  BTNode* node2 = BuyNode(2);
	  BTNode* node3 = BuyNode(3);
	  BTNode* node4 = BuyNode(4);
	  BTNode* node5 = BuyNode(5);
	  BTNode* node6 = BuyNode(6);
	  BTNode* node7 = BuyNode(7);

	  node1->left = node2;
	  node1->right = node4;
	  node2->left= node3;
	  node4->left = node5;
	  node4->right = node6;
	  //node3->right = node7;

	  return node1;
  }
  void PreOreder(BTNode* root) //根 左子树 右子树 
  {
	  if (root == NULL)
	  {
		  printf("NULL ");
		  return;
	  }
	  printf("%d ", root->data);
	  PreOreder(root->left);
	  PreOreder(root->right);
  }
  void InOreder(BTNode* root) //中序遍历 左子树 根 右子树
  {
	  if (root == NULL)
	  {
		  printf("NULL ");
		  return;
	  }
	  InOreder(root->left);
	  printf("%d ", root->data);
	  InOreder(root->right);
  }

  int main()
  {
	  BTNode* root = CreateTree();
	/*  PreOreder(root);*/
	  InOreder(root);
	  PostOreder(root);
	  return 0;
  }

中序遍历递归展开图，以左子树为例，右子树并未画出

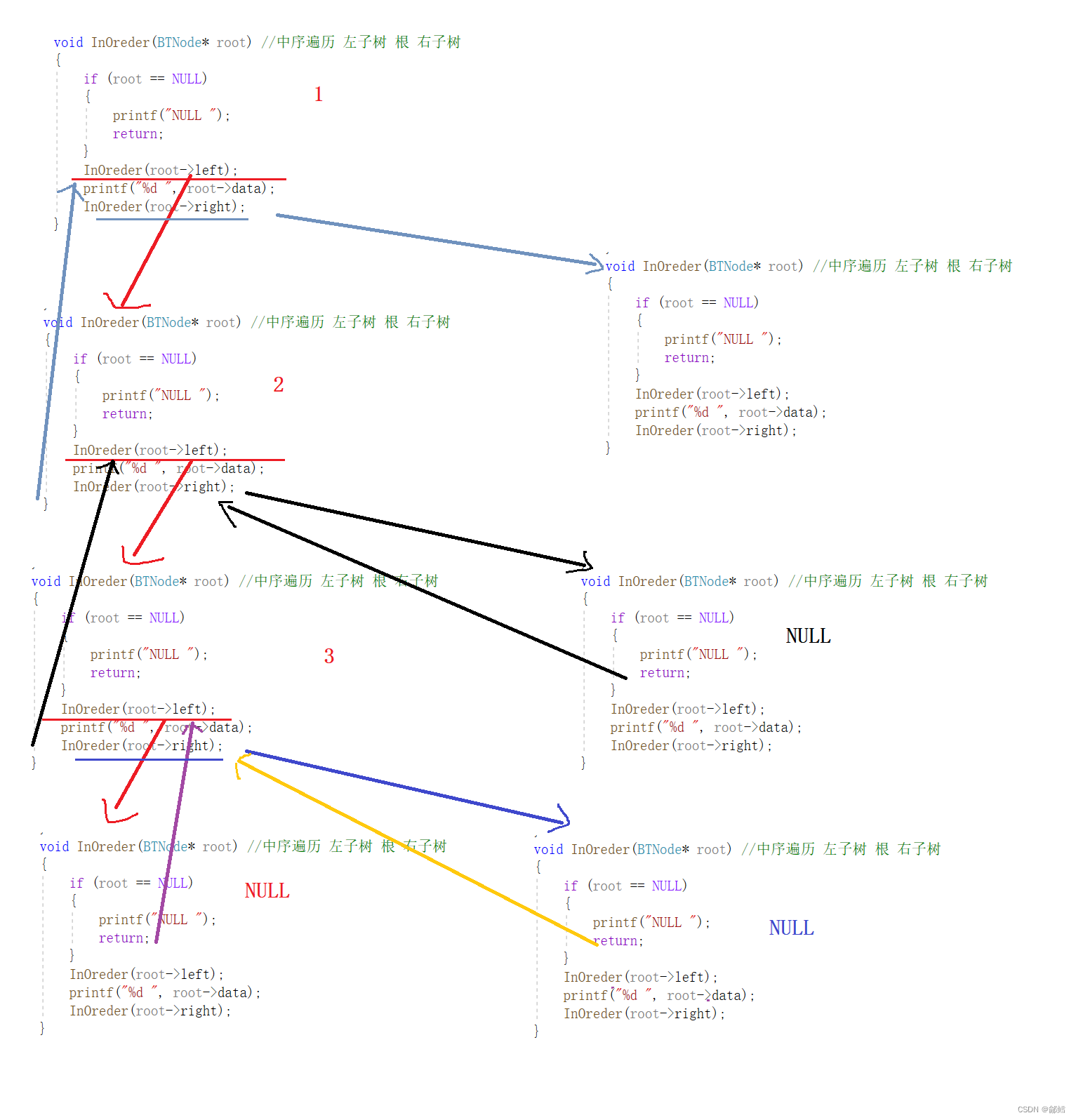
在这里插入图片描述

后序遍历

访问根结点的操作发生在遍历其左右子树之后
简单来说就是 左子树 右子树 根

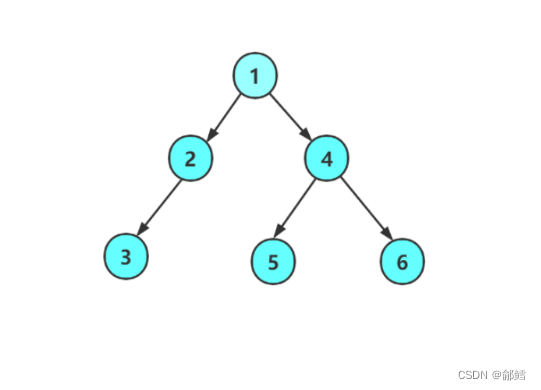
在这里插入图片描述

NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1

遇到节点1不能直接访问,得继续拆分,节点1又被分成根节点 (1)、左子树(2) 、右子树（4) ,遇到节点2不能直接访问,得继续拆分,节点 2被分成根节点 (2)、左子树(3) 、右子树（NULL) ,遇到节点3不能直接访问,得继续拆分,节点3又被分成根节点 (3)、左子树(NULL) 、右子树（NULL), 先访问3的左子树（NULL） ，再访问3的右子树（NULL） ，然后才到根节点（3），3这一整棵树走完了。2的左子树访问完了 ，再访问2的右子树（NULL）了，然后才到根节点（2）。2的整棵树作为1的左子树, ,2这一整棵树走完了 ，就走到节点1，但是遇到节点1不能直接访问,然后走到1的右子树（4），但是遇到节点4不能直接访问 得继续拆分，节点 4 又被分成根节点 (4)、左子树(5) 、右子树（6)，来到4的左子树节点5，还是不能直接访问 ，得继续拆分，节点 5 又被分成根节点 (5)、左子树(NULL) 、右子树（NULL) ，先访问5的左子树（NULL） ，再访问5的右子树（NULL） ，然后才到根节点（5），5这一整棵树走完了。4的左子树访问完了 ，再访问4的右子树（6）了，遇到节点6不能直接访问,得继续拆分,节点 6又被分成根节点 (6)、左子树(NULL) 、右子树（NULL)，先访问6的左子树（NULL） ，再访问6的右子树（NULL），然后才到根节点（6），6的整棵树作为4的右子树, ,6这一整棵树走完了 ，就走到节点4， 4的整棵树作为1的右子树, ,4这一整棵树走完了 ，就走到节点1

  BTNode* CreateTree()
  {
	  BTNode* node1 = BuyNode(1);
	  BTNode* node2 = BuyNode(2);
	  BTNode* node3 = BuyNode(3);
	  BTNode* node4 = BuyNode(4);
	  BTNode* node5 = BuyNode(5);
	  BTNode* node6 = BuyNode(6);
	  BTNode* node7 = BuyNode(7);

	  node1->left = node2;
	  node1->right = node4;
	  node2->left= node3;
	  node4->left = node5;
	  node4->right = node6;
	  //node3->right = node7;

	  return node1;
  }
  void PreOreder(BTNode* root) //根 左子树 右子树 
  {
	  if (root == NULL)
	  {
		  printf("NULL ");
		  return;
	  }
	  printf("%d ", root->data);
	  PreOreder(root->left);
	  PreOreder(root->right);
  }
  void InOreder(BTNode* root) //中序遍历 左子树 根 右子树
  {
	  if (root == NULL)
	  {
		  printf("NULL ");
		  return;
	  }
	  InOreder(root->left);
	  printf("%d ", root->data);
	  InOreder(root->right);
  }

  PostOreder(BTNode* root) // 后序遍历 左子树 右子树 根
  {
	  if (root == NULL)
	  {
		  printf("NULL ");
		  return;
	  }
	  PostOreder(root->left);
	  PostOreder(root->right);
	  printf("%d ", root->data);
  }

  int main()
  {
	  BTNode* root = CreateTree();
	/*  PreOreder(root);*/
	  InOreder(root);
	  PostOreder(root);
	  return 0;
  }

层序遍历

1 2 3 4 5 6

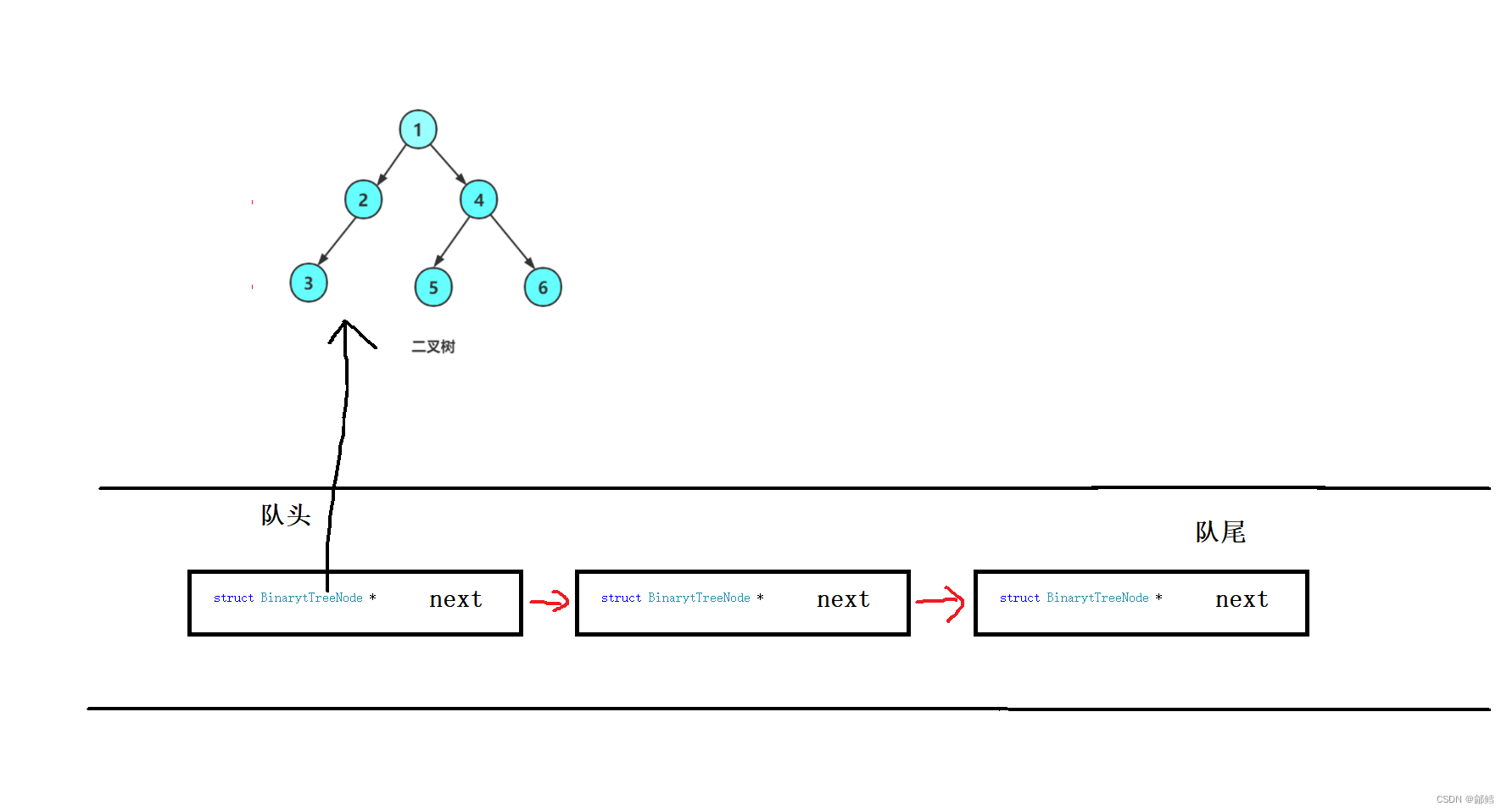
层序遍历使用队列先进先出的特性，二叉树的上一层 出队，二叉树的下一层入队

根节点1入队 ,然后1节点出队 ，再把1节点的左孩子2 、右孩子4入队 ， 再2节点出队 ，2的左孩子3入队 ，2的右孩子空树 ，空树就不入队了 ,4出队 ，4的左孩子5入队 ，右孩子6入队 ,
最后3出队 ，左右孩子都是空树就不入队了,5出队 ，左右孩子都是空树就不入队了,6出队 ，左右孩子都是空树就不入队了, 当所有节点出队也就结束了
在这里插入图片描述

void LevelOrder(BTNode* root) //层序遍历 
{
	
	Queue q;
	QueueInit(&q);
	//遍历 
	//不是空树 
	if (root)
		QueuePush(&q ,root);
	while (!QueueEmpty(&q) )
	{
		
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ",front->data);
		 
			if (front->left)//不是空树 入队
		{
			QueuePush(&q, front->left);

		}
		if (front->right) //不是空树 入队
		{
			QueuePush(&q, front->right);

		}

	}

	QueueDestory(&q);
}

树节点个数

采用分治方法

分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。
分治策略是：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。

typedef int BinartTreeType;
typedef struct BinarytTreeNode
{
	BinartTreeType data;//节点存放的数据
	struct BinarytTreeNode* left; //指向当前节点的左孩子
	struct BinarytTreeNode* right;//指向当前节点的右孩子

}BTNode;

BTNode* BuyNode(BinartTreeType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		printf("malloc fail");
		exit(-1);
	}
	//扩容成功
	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;

}
BTNode* CreateTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	BTNode* node7 = BuyNode(7);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	//node3->right = node7;

	return node1;
}

//int TreeSize(BTNode* root, int* psize)
//{
//	if (root == NULL)
//		return;
//	(*psize)++;
//	TreeSize(root->left, psize);
//	TreeSize(root->right, psize);
//}

int TreeSize(BTNode* root) //分治思想
{
	return root == NULL ? 0 :
			TreeSize(root->left ) 
			+TreeSize(root->right)
			+ 1; //  +1 是加上自己

}

int main()
{
	BTNode* root = CreateTree();
	printf("%d ", TreeSize(root));
	return 0;
}

在这里插入图片描述

树的深度

采用分治思想 ，求出最长的那一条
当前树的高度 = 左右子树高度大的+1

typedef int BinartTreeType;
typedef struct BinarytTreeNode
{
	BinartTreeType data;//节点存放的数据
	struct BinarytTreeNode* left; //指向当前节点的左孩子
	struct BinarytTreeNode* right;//指向当前节点的右孩子

}BTNode;

BTNode* BuyNode(BinartTreeType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		printf("malloc fail");
		exit(-1);
	}
	//扩容成功
	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;

}
BTNode* CreateTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	BTNode* node7 = BuyNode(7);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	//node3->right = node7;

	return node1;
}
//int TreeHight(BTNode* root) //求整棵树的高度
//{
//	if (root == NULL)
//	{
//		return 0;
//	}
//	return TreeHight(root->left) > TreeHight(root->right) 
//		? TreeHight(root->left) + 1: TreeHight(root->right) + 1;
//}

int TreeHeight(BTNode* root)
{
	if( root == NULL)
		return 0;
	 
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight 
		? leftHeight + 1
		: rightHeight + 1;

}

int main()
{
	BTNode* root = CreateTree();
	printf("%d ", TreeHeight(root));

	return 0;
}

在这里插入图片描述

第K层节点个数

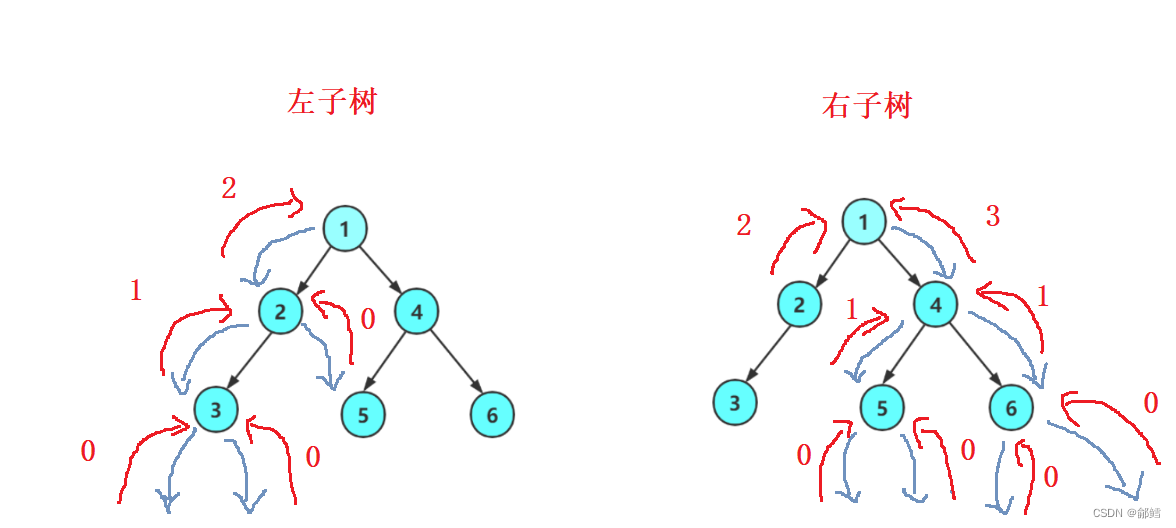
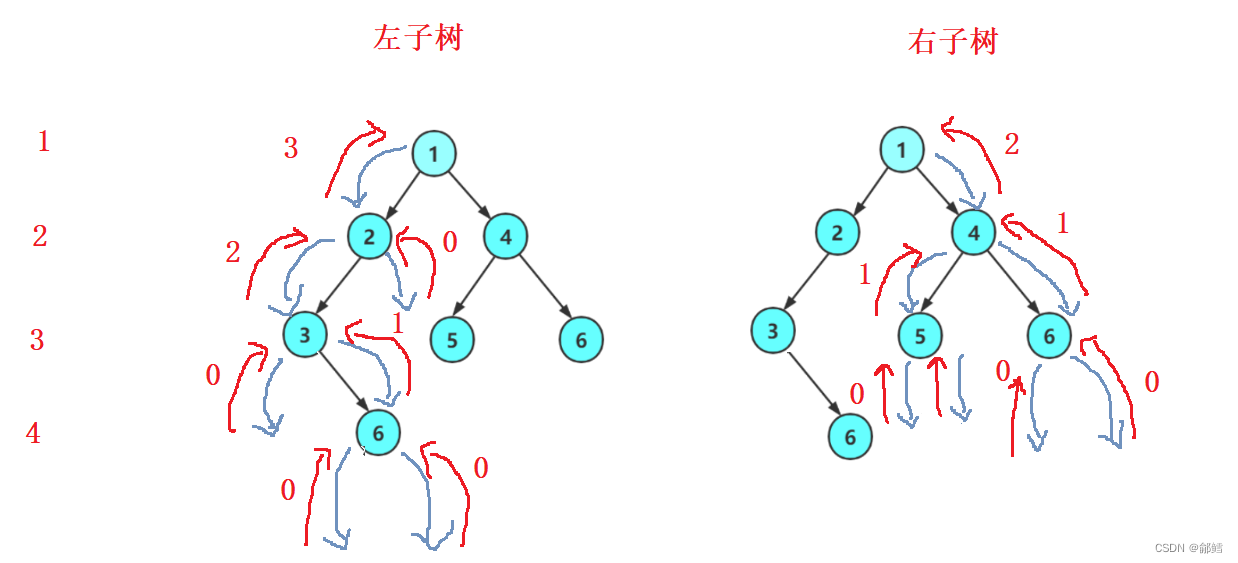
根的第K层节点个数 = 左子树的第K-1层个数 + 右子树的第K-1 层个数

typedef int BinartTreeType;
typedef struct BinarytTreeNode
{
	BinartTreeType data;//节点存放的数据
	struct BinarytTreeNode* left; //指向当前节点的左孩子
	struct BinarytTreeNode* right;//指向当前节点的右孩子

}BTNode;

BTNode* BuyNode(BinartTreeType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		printf("malloc fail");
		exit(-1);
	}
	//扩容成功
	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;

}
BTNode* CreateTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	BTNode* node7 = BuyNode(7);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	node3->right = node7;

	return node1;
}
int TreeKlevel(BTNode* root,int k) //第K层节点个数
{
	if (root == NULL)
		return 0;
	if (k == 1)  // 隐含root != NULL ， 此时是第K层
		return 1;
	//左子树 K-1 个数 + 右子树K-1 个数 
	int leftKlevel = TreeKlevel(root->left, k - 1);
	int rightKlevel = TreeKlevel(root->right, k - 1);
	return leftKlevel + rightKlevel;

}
int main()
{
	BTNode* root = CreateTree();
	int k = 3;
	printf("%d ", TreeKlevel(root,k));

	return 0;
}

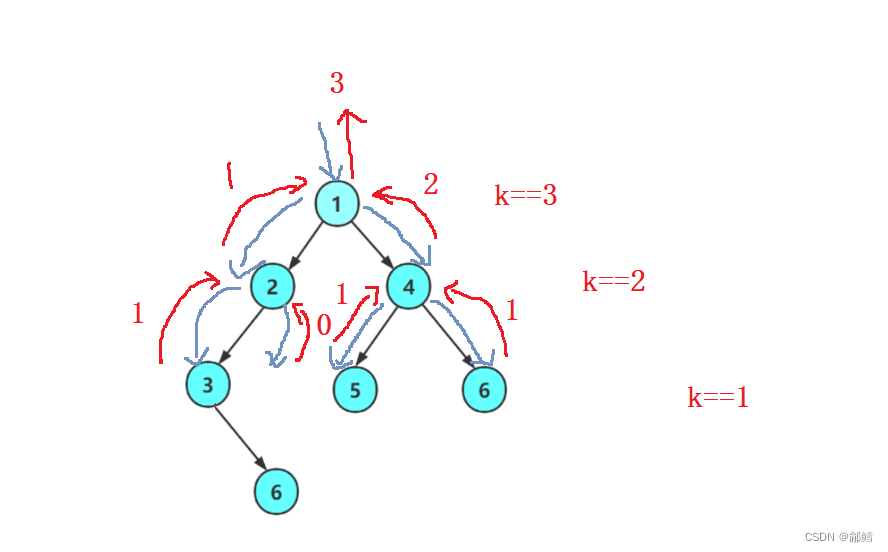
在这里插入图片描述

查找二叉树中的元素

BTNode* BinaryTreeFind(BTNode* root , BinartTreeType x )//查找二叉树中的元素
{
	//左子树 右子树 根
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	//保存
	BTNode* lret = BinaryTreeFind(root->left, x);
	if (lret)
		return lret;
	//保存
	BTNode* rret = BinaryTreeFind(root->right, x);
	if (rret)
		return rret;
	//没有找到
	return NULL;
}

递归展开图：

0c.png)
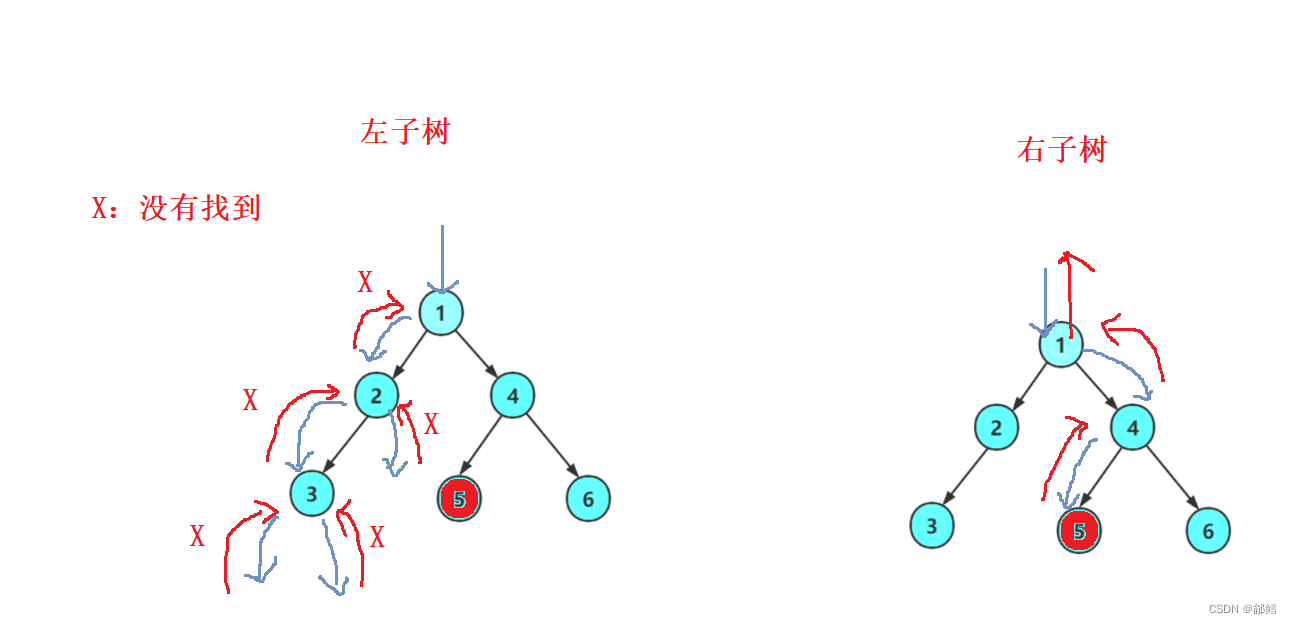
在这里插入图片描述

完整代码
Test.c

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include"Queue.h"
typedef int BinartTreeType;
typedef struct BinarytTreeNode
{
	BinartTreeType data;//节点存放的数据
	struct BinarytTreeNode* left; //指向当前节点的左孩子
	struct BinarytTreeNode* right;//指向当前节点的右孩子

}BTNode;

BTNode* BuyNode(BinartTreeType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		printf("malloc fail");
		exit(-1);
	}
	//扩容成功
	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;

}
BTNode* CreateTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);
	BTNode* node7 = BuyNode(7);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	node3->right = node7;

	return node1;
}
//void PreOreder(BTNode* root) //根 左子树 右子树 
//{
//	if (root == NULL)
//	{
//		printf("NULL ");
//		return;
//	}
//	printf("%d ", root->data);
//	PreOreder(root->left);
//	PreOreder(root->right);
//}
//void InOreder(BTNode* root) //中序遍历 左子树 根 右子树
//{
//	if (root == NULL)
//	{
//		printf("NULL ");
//		return;
//	}
//	InOreder(root->left);
//	printf("%d ", root->data);
//	InOreder(root->right);
//}
//
//void PostOreder(BTNode* root) // 后序遍历 左子树 右子树 根
//{
//	if (root == NULL)
//	{
//		printf("NULL ");
//		return;
//	}
//	PostOreder(root->left);
//	PostOreder(root->right);
//	printf("%d ", root->data);
//}
//int TreeSize(BTNode* root, int* psize)
//{
//	if (root == NULL)
//		return;
//	(*psize)++;
//	TreeSize(root->left, psize);
//	TreeSize(root->right, psize);
//}
//
//int TreeSize(BTNode* root) //分治思想
//{
//	return root == NULL ? 0 :
//		TreeSize(root->left)
//		+ TreeSize(root->right)
//		+ 1; // +1 是加上自己
//
//}

//int TreeHight(BTNode* root) //求整棵树的高度
//{
//	if (root == NULL)
//	{
//		return 0;
//	}
//	return TreeHight(root->left) > TreeHight(root->right) 
//		? TreeHight(root->left) + 1: TreeHight(root->right) + 1;
//}

//int TreeHeight(BTNode* root)
//{
//	if( root == NULL)
//		return 0;
//	 
//	int leftHeight = TreeHeight(root->left);
//	int rightHeight = TreeHeight(root->right);
//
//	return leftHeight > rightHeight 
//		? leftHeight + 1
//		: rightHeight + 1;
//
//}
//int TreeKlevel(BTNode* root,int k) //第K层节点个数
//{
//	if (root == NULL)
//		return 0;
//	if (k == 1)  // 隐含root != NULL ， 此时是第K层
//		return 1;
//	//左子树 K-1 个数 + 右子树K-1 个数 
//	int leftKlevel = TreeKlevel(root->left, k - 1);
//	int rightKlevel = TreeKlevel(root->right, k - 1);
//	return leftKlevel + rightKlevel;
//
//}

BTNode* BinaryTreeFind(BTNode* root , BinartTreeType x )//查找二叉树中的元素
{
	//左子树 右子树 根
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	//保存
	BTNode* lret = BinaryTreeFind(root->left, x);
	if (lret)
		return lret;
	//保存
	BTNode* rret = BinaryTreeFind(root->right, x);
	if (rret)
		return rret;
	//没有找到
	return NULL;
}

void LevelOrder(BTNode* root) //层序遍历 
{
	
	Queue q;
	QueueInit(&q);
	//遍历 
	//不是空树 
	if (root)
		QueuePush(&q ,root);
	while (!QueueEmpty(&q) )
	{
		
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ",front->data);
		 
			if (front->left)//不是空树 入队
		{
			QueuePush(&q, front->left);

		}
		if (front->right) //不是空树 入队
		{
			QueuePush(&q, front->right);

		}

	}

	QueueDestory(&q);
}

int main()
{
	BTNode* root = CreateTree();
	/*  PreOreder(root);*/
	 // InOreder(root);
	 // PostOreder(root);

	//int size1 = 0;
	//TreeSize(root, &size1);
	//printf("%d ", size1);
	//printf("%d ", TreeSize(root));
	//printf("%d ", TreeHeight(root));
	/*int k = 3;
	printf("%d ", TreeKlevel(root,k));*/
	/*printf("%p ", BinaryTreeFind(root, 2));*/
	LevelOrder(root);
	return 0;
}

Queue.h

#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<assert.h>

typedef struct BinarytTreeNode *  QueueNodeTypeData;

typedef struct  QueueNode
{
	struct  QueueNode* next;
	QueueNodeTypeData data;
}QueueNodeType;

typedef struct Queue
{
	QueueNodeType * tail; // 队尾
	QueueNodeType * head; //队头
	int size; 
} Queue;  // 链式结构：表示队列


void QueueInit(Queue* pq);  // 初始化  

void QueueDestory(Queue* pq); //队列的销毁

void QueuePush(Queue* pq , QueueNodeTypeData x );  // 队尾入队列

void QueuePop(Queue* pq); //队头出队列

int QueueSize(Queue* pq);//获取队列中有效元素个数

bool QueueEmpty(Queue* pq); // 判断队列是否为空 

QueueNodeTypeData QueueFront(Queue* pq); //获取队列头部元素

QueueNodeTypeData QueueBack(Queue* pq); //获取队列尾部元素

Queue.c

#include"Queue.h"
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QueueDestory(Queue* pq) //队列的销毁
{
	assert(pq);
	QueueNodeType * cur = pq->head;
	
	//遍历 
	while (cur)
	{
		QueueNodeType* next = cur->next;  //保存下一个节点的地址
		free(cur); //释放当前节点
		cur = next; 
	}
	  pq->tail = pq->head = NULL;
	pq->size = 0;
}
void QueuePush(Queue* pq, QueueNodeTypeData x) // 入队 
{
	assert(pq);
	QueueNodeType* newnode =(QueueNodeType*) malloc( sizeof(QueueNodeType) );
	if (newnode == NULL)
	{
		printf(" malloc fail");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	//扩容成功

	//第一次入队
	if ( pq->head == NULL)
	{
   		assert(pq->tail == NULL);   //pq->head ==NULL , pq->tail != NULL ,就是出问题了
		pq->tail = pq->head = newnode;
	}
	else //非第一次入队
	{
		pq->tail->next = newnode; // 类似尾插
		pq->tail = newnode; // 更新tail 指针
	}
	pq->size++;
}
void QueuePop(Queue* pq) //队头出队列
{
	assert(pq);
	assert(pq->head != NULL); 

	//只有一个节点

	if (pq->head->next == NULL) 
	{
		free(pq->tail);  //出队
		pq->tail = pq->head = NULL;
	}
	// 多个节点
	else
	{
		QueueNodeType* next = pq->head->next; // 保存下一个节点的地址 
		free(pq->head); // 出队
		pq->head = NULL;
		pq->head = next;  //更新pq->head ，往后走 
	}
	pq->size--;
}


int QueueSize(Queue* pq)//获取队列中有效元素个数
{
	assert(pq);
	
	return pq->size;
}

//bool QueueEmpty(Queue* pq) // 判断队列是否为空 
//{
//	assert(pq);
//
//	if (pq->head == 0)
//	{
//		return true;
//	}
//	else
//	{
//		return false;
//	}
//}

bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->size == 0;
}

QueueNodeTypeData QueueFront(Queue* pq) //获取队列头部元素
{
	assert(pq);
	assert(!QueueEmpty(pq)); //防止队列为空
	
	return pq->head->data;

}

QueueNodeTypeData QueueBack(Queue* pq) //获取队列尾部元素
{
	assert(pq);
	assert(!QueueEmpty(pq)); //防止队列为空

	return pq->tail->data;
}

在这里插入图片描述

如果你觉得这篇文章对你有帮助，不妨动动手指给点赞收藏加转发，给鄃鳕一个大大的关注
你们的每一次支持都将转化为我前进的动力！！！


http://www.kler.cn/a/5857.html

相关文章：

  • 计算机毕业设计Python机器学习农作物健康识别系统 人工智能 图像识别 机器学习 大数据毕业设计 算法
  • ThreadLocal 的使用场景
  • 【可实战】Bug的判定标准、分类、优先级、定位方法、提交Bug（包含常见面试题）
  • 第四、五章补充：线代本质合集（B站：小崔说数）
  • QT自定义工具条渐变背景颜色一例
  • mysql中查询json的技巧
  • 【数据库管理】①实例与数据库
  • Springboot: Tomcat很好我选Undertow
  • ShareSDK Android 第三方平台分享参数说明
  • MySQL - 基于SSL安全连接的主从复制
  • 蓝桥杯31天真题冲刺|题解报告|第二十三天
  • Python中编码【encode】解码【decode】讲解
  • k8s qos等级
  • 【Windows版】VScode配置C++开发环境
  • Python实现提前查询考研成绩
  • 大家有没有时候觉得，递归，分治，回溯，傻傻分不清楚？
  • 设计LFU缓存结构（美团面试算法题）
  • 骨传导蓝牙耳机什么牌子，推荐几款比较热销的骨传导耳机
  • 【Elastic (ELK) Stack 实战教程】04、ElasticSearch 集群进阶及优化
  • Java-双向链表的实现
  • 【软件设计师03】数据库系统
  • 电路板焊接技巧实践（没有电烤箱条件下）
  • 人工智能交互革命：探索ChatGPT的无限可能 第13章ChatGPT的应用场景和创新应用
  • 智慧办公抉择之——VBA与Python的选择
  • MySQL尚硅谷学习笔记之DQL语言
  • QT开发笔记（USB Bluetooth）