堆的实现

HeapPush插入

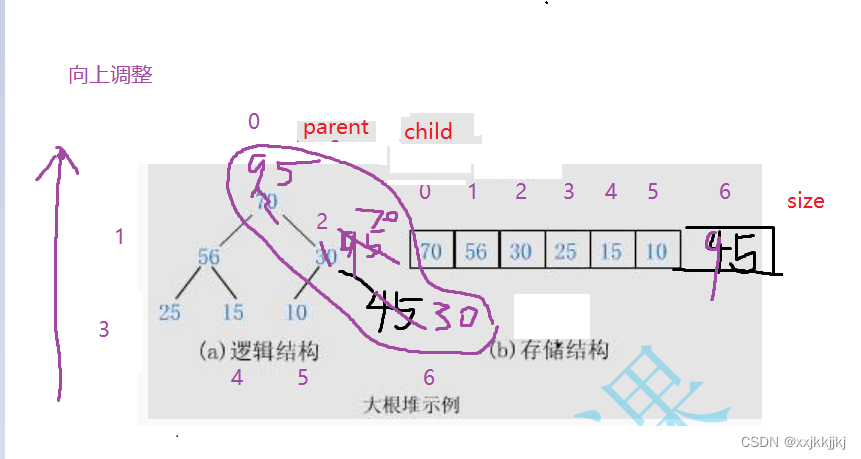
 parent = (child-1)/2

leftchild = parent* 2+1

rightchild = parent* 2+2
根据此规律可以父子节点可以在数组中相互找到
逻辑上是完全二叉树，存储结构也就是底层是个顺序表

 void AdjustUp(HPDataType* a, int child)

// 除了child这个位置，前面数据构成堆     时间复杂度log(N) 高度次  
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)//parent>=0 经典错误水管漏水
	{
		if (a[child] > a[parent])//大堆用大于，方便更改
		{
			Swap(&a[child],&a[parent]);
			child = parent;
			parent = (child - 1) / 2;//这里写child更好理解,计算的是新孩子的父亲
		}
		else
		{
			break;
		}
	}
}

void HeapPush(Heap* php, HPDataType x)
{
	assert(php);

	if (php->size == php->capacity)
	{
		HPDataType* tmp = (HPDataType*)realloc(php->a,sizeof(HPDataType) * php->capacity * 2);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity *= 2;
	}
	php->a[php->size++] = x;

	AdjustUp(php->a,php->size-1);//size-1是孩子下标
}

HeapPop删除

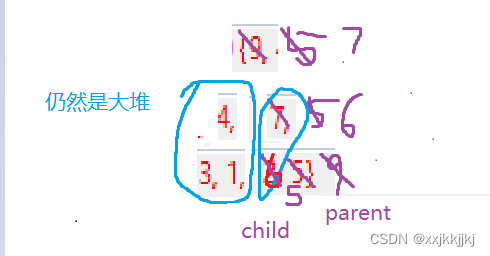
pop掉尾很简单size--就可以但是对于堆来说没什么意义

大堆要Pop最大的值
步骤:

把堆顶下标0换到数组size-1的位置,size--
原来的size-1的数据破坏了大堆，要继续从 根也就是下标为0的位置向下调整，

parent要小于较大的那个child就交换   

大堆就与较大的子结点交换，小堆就与较小的子节点交换（因为要保证大堆或小堆）

直到调整到叶子，或者parent > child就结束

void HeapPop(Heap* php)

//使用前提：左右子树都是大堆/小堆   时间复杂度log(N) 高度次       
void AdjustDown(HPDataType* a, int n, int parent)
{
	//默认左孩子大，更方便
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 选出左右孩子中大的那一个
		if (child + 1 < n && a[child + 1] < a[child])
		{
			++child;//右孩子存在且>左孩子
		}
		if (a[child] < a[parent])//大堆用大于，方便更改
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(Heap* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	//删除数据
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

并且要注意 向上调整 和向下调整的前提

向上调整 ：除了child这个位置，前面数据构成堆

向下调整：左右子树都是大堆/小堆

 代码实现是注意一下

不必定义左右孩子，那样会冗余，判断多
利用leftchild + 1 = rightchild 就能找到右孩子

如果右孩子存在且大于左孩子，那么就只定义一个child，让child ＋1就是右孩子
 

堆排序实现

上面只是堆的实现，并不是堆排序，不会因为排序而创建一个堆的结构，得不偿失。

可以利用向上调整或者向下调整 建一个堆

并且在这里 排升序需要建立 大堆，降序就用小堆

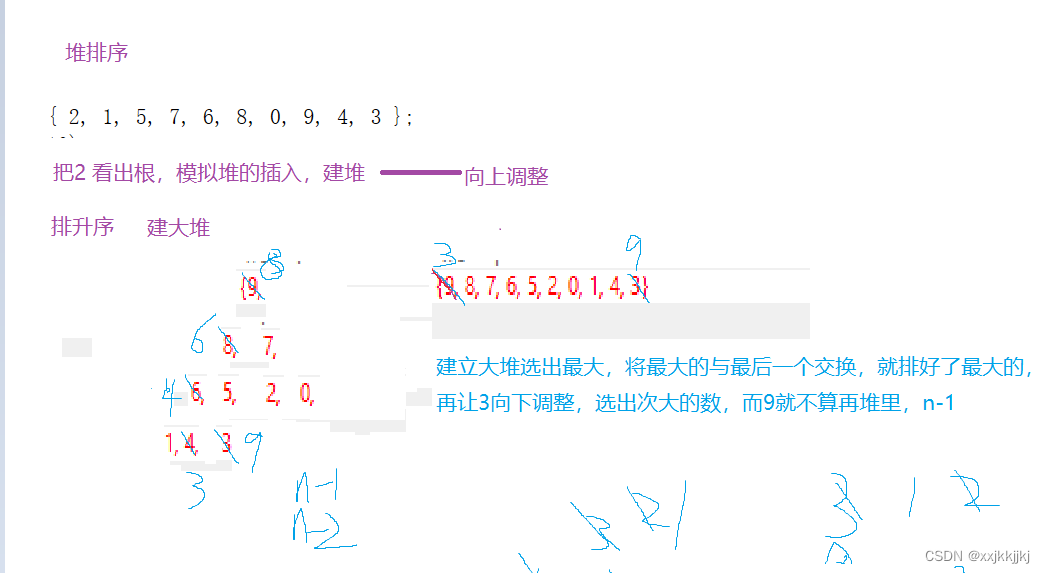
向上调整就是 把第一个数看作根，从1到N-1 模拟堆的插入 建堆

时间复杂度是NlogN

而向下调整建堆 时间复杂度是O（N）

所以用向下调整

向下调整建堆 

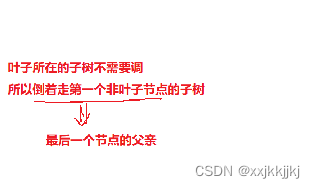
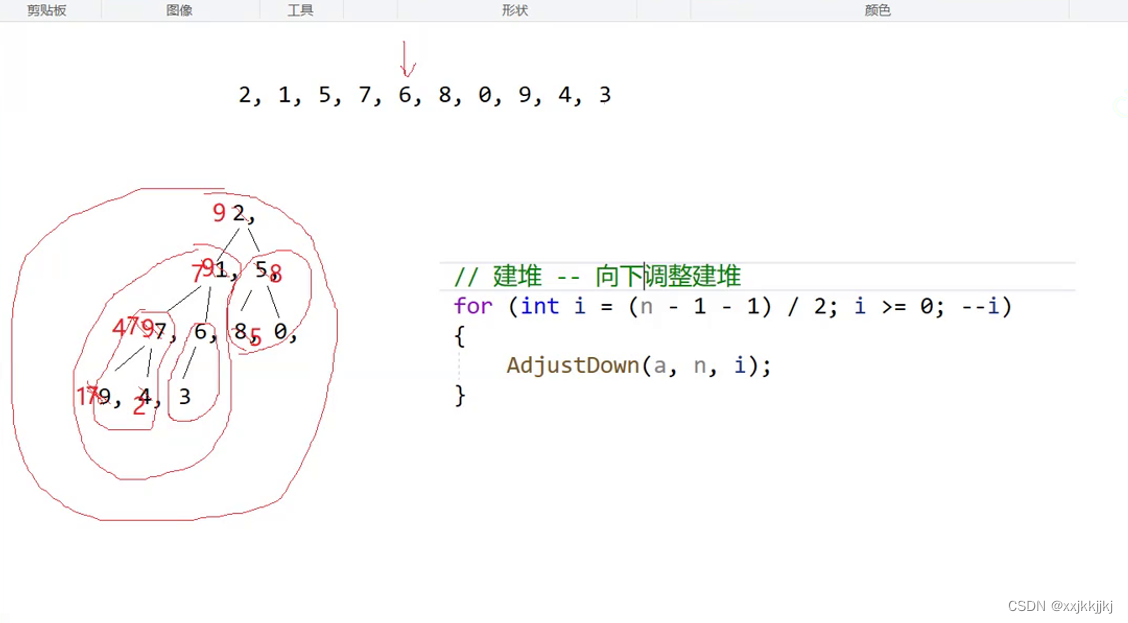
不需要从叶子开始调整，因为叶子可以看作大堆和小堆，

（叶子之后无孩子）向下调整叶子结点无意义

需要从第一个非叶子结点开始调整直到调整到根（2），第一个非叶子结点也就是最后一个结点的parent

建立大堆选出最大，将最大的与最后一个交换，就排好了最大的，再让3向下调整，选出次大的数，而9就不算再堆里，控制n-1  n-2

//排升序-建大堆 排降序-建小堆
void HeapSort(int* a, int n)
{
	//建堆--向上调整建堆 -- O(N*logN)
	/*for (int i = 1; i < n; i++)
	{
		AdjustUp(a, i);
	}*/

	//建堆--向下调整建堆 -- O(N)
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a,n,i);
	}

	int end = n - 1;//end正好是前面数据个数
	while(end>0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
	
}

如果排升序建小堆的坑

TopK