Tensor张量基础与常用方法【Pytorch】
Tensor中文译名为张量,标量是零维张量,向量是一维张量,矩阵是二维张量,矩阵的堆叠是三维张量……
张量的维数可以无穷大,不过由于现实世界是三维的,因此更高维度的图形我们无法想象,但是这并不妨碍我们对高维张量的使用
1. Tensor数据类型
| 数据类型 | dtype【Tensor的属性】 | CPU Tensor类型 | GPU Tensor类型 |
|---|---|---|---|
16位浮点数 | torch.float16或torch.half | torch.HalfTensor | torch.cuda.HalfTensor |
32位浮点数 | torch.float32或torch.float | torch.FloatTensor | torch.cuda.FloatTensor |
64位浮点数 | torch.float64或torch.double | torch.DoubleTensor | torch.cuda.DoubleTensor |
8位无符号整数 | torch.uint8 | torch.ByteTensor | torch.cuda.ByteTensor |
8位有符号整数 | torch.int8 | torch.CharTensor | torch.cuda.CharTensor |
16位有符号整数 | torch.int16或torch.short | torch.ShortTensor | torch.cuda.ShortTensor |
32位有符号整数 | torch.int32或torch.int | torch.IntTensor | torch.cuda.IntTensor |
64位有符号整数 | torch.int64或torch.long | torch.LongTensor | torch.cuda.LongTensor |
2. Tensor创建
-
torch.Tensor(维度):创建指定维度的Tensor,创建后会有随机初始值,数据类型是torch.FloatTensorimport torch # 创建维度(2,2)的Tensor x = torch.Tensor(2, 2) print(x)
torch.CPU Tensor类型(维度):创建指定维度的Tensor,依旧有初始值,不过数据类型由方法名确定# 创建维度(2,2)的Tensor,不过数据类型为IntTensor y = torch.IntTensor(2, 2) print(y.type())
-
torch.Tensor(list):通过传入的list对Tensor内容初始化import torch l = list([[1, 2], [3, 4]]) # 利用l的内容进行初始化,若想换个数据类型则使用此类型对应的函数构造 x = torch.Tensor(l) print(x)
2.1 特殊布局Tensor创建
使用内置方法创建
Tensor时数据类型默认都是FloatTensor,如果需要转换类型,可以使用如下方法👇
import torch
l = list([[1, 1], [2, 2]])
x = torch.Tensor(l)
# 将x转换为torch.IntTensor类型
# 同样的,还有float(),double(),half()等方法可以进行对应转换
x = x.int()
print(x)

-
torch.zeros(维度):创建元素全为0的Tensorimport torch # 创建维度(2,2)的Tensor,不指定类型时默认都是FloatTensor,后续不再说明 x = torch.zeros(2,2) print(x)
-
torch.eye(维度):创建对角线位置全1,其余位置全0的Tensorimport torch # 创建维度(3,3)的Tensor x = torch.eye(3, 3) print(x)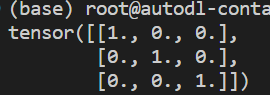
-
torch.ones(维度):创建元素全为1的Tensorimport torch x = torch.ones(3, 3) print(x)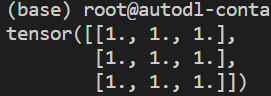
-
torch.rand(维度):创建将元素初始化为区间[0,1)的随机数Tensortorch.randn(维度):创建符合正态分布的随机数Tensorimport torch x = torch.rand(3, 3) print(x)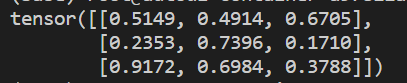
-
torch.arange(start,end,step):创建一个在区间[start,end)按指定步长step递增的一维Tensorimport torch # 从1开始递增,步长为0.5,最后一个元素小于4 x = torch.arange(1, 4, 0.5) print(x)
-
torch.linspace(start,end,parts):创建一个在区间[start,end]被均匀划分为parts份的一维Tensorimport torch # 第一个元素是0,最后一个元素是10 # 总共要划分为5个元素,实际上间隔有4个,因此步长=(end-start)/4=2.5 x = torch.linspace(0, 10, 5) print(x)
-
torch.from_numpy(ndarray):将Numpy的ndarray对象转换为Tensorimport torch import numpy as np arr = np.array([[1, 2], [3, 4]]) # 转换后的 Tensor 数据类型与 ndarry 一致 x = torch.from_numpy(arr) print(x)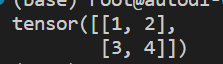
3. Tensor数学操作
下述方法操作后都需要原对象接受才能发挥作用,方法通常有两种使用方式,一者是
Tensor对象.xxx,一者是torch.xxx,使用过程试一下就知道怎么回事了
| 方法 | 说明 |
|---|---|
torch.add(a,n) | 张量a中每个元素加n,或与另一个张量n【维度相同】逐元素相加 |
torch.mul(a,n) | 张量a中每个元素乘n,或与另一个张量n【维度相同】逐元素相乘 |
torch.div(a,n) | 张量a中每个元素除n,或与另一个张量n【维度相同】逐元素相除 |
torch.fmod(a,n),torch.remainder(a,n) | 张量a中每个元素对n求余 |
torch.abs(a) | 张量a中的每个元素取绝对值 |
torch.ceil(a) | 张量a中的每个元素向上取整 |
torch.floor(a) | 张量a中的每个元素向下取整 |
torch.round(a) | 张量a中的每个元素取最近的整数【1.1取1,2.6取3】 |
torch.frac(a) | 张量a中每个元素的分数部分 |
torch.neg(a) | 张量a中每个元素取负 |
torch.reciprocal(a) | 张量a中每个元素取倒数 |
torch.log(a) | 张量a中每个元素的自然对数【以e为底】 |
torch.pow(a,n) | 张量a中的每个元素取n次方 |
torch.exp(a) | 张量a中的每个元素变为指数,底数为e得到新值 |
torch.sigmoid(a) | 张量a中的每个元素代入sigmoid函数 |
torch.sign(a) | 张量a中若为正数或0,则1代替;否则-1代替 |
torch.sqrt(a) | 张量a中的每个元素取算数平方根,负数则放置nan |
torch.dist(in,oth,p) | 张量in减去oth再求p范数【所有元素p次方之和再开p次方】 |
torch.mean(a) | 张量a中所有元素的均值 |
torch.norm(a) | 张量a的二范数【元素平方之和再开方】 |
torch.prod(a) | 张量a中所有元素之积 |
torch.sum(a) | 张量a中所有元素之和 |
torch.max(a) | 张量a中所有元素最大值 |
torch.min(a) | 张量a中所有元素最小值 |
torch.clamp(a,max,min) | 张量a中的元素大于max就取max,小于min就取min,其余不变 |
import torch
import numpy as np
l = list([[1, 2], [3, 4]])
x = torch.IntTensor(l)
# x中大于3的部分取3,小于2的部分取2
c = x.clamp(max=3, min=2)
print(c)

4. Tensor线性代数
需要操作张量的方法一般来说都会有两种形式,一种是
torch.xxx,一种是tensor对象.xxx,看个人习惯使用就好,后边不再说明
-
torch.dot(a,b):向量a与向量b的点积【也叫内积】,结果是一个数
a ⃗ ⋅ b ⃗ = a 1 b 1 + a 2 b 2 + . . . + a n b n = ∑ i = 1 n a i b i \vec{a}\cdot\vec{b}=a_1b_1+a_2b_2+...+a_nb_n=\sum_{i=1}^{n}a_ib_i a⋅b=a1b1+a2b2+...+anbn=i=1∑naibiimport torch a = torch.IntTensor([1, 2, 3]) b = torch.IntTensor([3, 2, 1]) # a向量与b向量点积 c = torch.dot(a, b) print(c)
-
torch.mv(a,b):实现矩阵a与向量b的乘法【不需要手动转置操作】
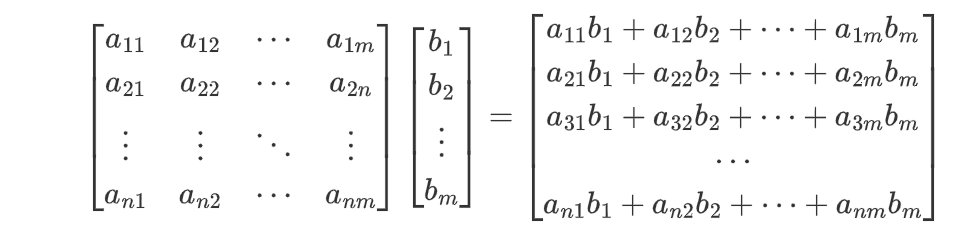
import torch a = torch.IntTensor([[1, 2, 3], [2, 3, 4], [3, 4, 5]]) b = torch.IntTensor([1, 2, 3]) # a矩阵与b向量相乘 c = torch.mv(a, b) print(c)
-
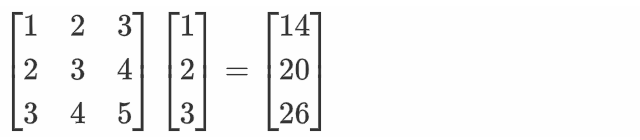
torch.mm(a,b):实现矩阵a与矩阵b相乘【矩阵乘法与向量类似,可以看作是多列向量】import torch a = torch.IntTensor([[1, 2, 3], [2, 3, 4], [3, 4, 5]]) b = torch.IntTensor([[2, 3, 4], [3, 4, 5], [4, 5, 6]]) # 矩阵a的第i行与矩阵b的第j列元素点积结果作为c矩阵第i行第j列的元素 c = torch.mm(a, b) print(c)
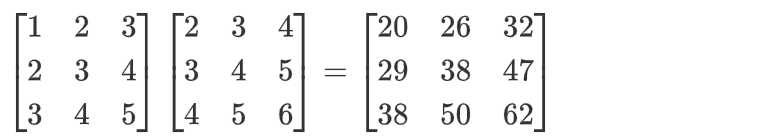
| 方法 | 说明 |
|---|---|
torch.addmm(c,a,b) | 矩阵a与矩阵b相乘加上矩阵c |
torch.addmv(b, a, c) | 矩阵a与向量b相乘加上向量c【向量是一维张量】 |
torch.addr(c,a,b) | 向量a与向量b求外积【列向量乘行向量】加上矩阵c |
torch.bmm(b1,b2) | 两个batch内的矩阵进行批矩阵乘法【目前不知道啥意思】 |
torch.ger(a,b) | 求向量a与向量b的外积【即列向量与行向量相乘】 |
torch.inverse(a) | 求方阵a的逆矩阵 |
torch.addbmm(t,b1,b2) | 将两个batch内的矩阵b1,b2进行批矩阵乘法操作并累加,其结果与矩阵t相加 |
torch.baddbmm(t,b1,b2) | 将两个batch内的矩阵b1,b2进行批矩阵乘法操作,结果与另一batch内的矩阵t相加 |
torch.eig(a,eigenvectors=True) | 得到方阵a特征值以及对应的特征向量 |
特征分解中,矩阵分解形式为: A = Q ⋀ Q − 1 其中 Q 与 Q − 1 互为逆矩阵,并且 Q 的列就是 A 的特征值所对应的特征向量 而 ⋀ 为矩阵 A 的特征值组成的对角矩阵 特征分解中,矩阵分解形式为:\\ A=Q \bigwedge Q^{-1} \\ 其中Q与Q^{-1}互为逆矩阵,并且Q的列就是A的特征值所对应的特征向量\\ 而\bigwedge为矩阵A的特征值组成的对角矩阵 特征分解中,矩阵分解形式为:A=Q⋀Q−1其中Q与Q−1互为逆矩阵,并且Q的列就是A的特征值所对应的特征向量而⋀为矩阵A的特征值组成的对角矩阵
import torch
a = torch.Tensor([[-1, 1, 1], [1, -1, 1], [1, 1, -1]])
# eigenvectors参数为True才能得到特征向量
# 求a矩阵的特征值与特征向量
b = torch.eig(a, eigenvectors=True)
print(b)

特征值
x
1
=
−
2
,对应的特征向量为
e
i
g
e
n
v
e
c
t
o
r
s
中第一列元素,即
[
−
0.8165
0.4082
0.4082
]
同理,特征值
x
2
=
1
与
x
3
=
−
2
对应的对应的特征向量为
e
i
g
e
n
v
e
c
t
o
r
s
中第二、三列元素
特征值x_1=-2,对应的特征向量为eigenvectors中第一列元素,即 \begin{bmatrix} -0.8165\\ 0.4082\\ 0.4082 \end{bmatrix}\\ 同理,特征值x_2=1与x_3=-2对应的对应的特征向量为eigenvectors中第二、三列元素
特征值x1=−2,对应的特征向量为eigenvectors中第一列元素,即
−0.81650.40820.4082
同理,特征值x2=1与x3=−2对应的对应的特征向量为eigenvectors中第二、三列元素
想要验证说法是否正确,只需要拼凑出
Q
⋀
Q
−
1
Q⋀Q^{-1}
Q⋀Q−1,若结果能够得到A,则说明我们这个过程是正确的
import torch
# 原矩阵A
a = torch.Tensor([[-1, 1, 1], [1, -1, 1], [1, 1, -1]])
# 对矩阵A求特征值与特征向量
b = torch.eig(a, eigenvectors=True)
# 得到特征向量组成的矩阵Q
Q = b.eigenvectors
# 得到Q矩阵的逆矩阵
Q_inverse = torch.inverse(Q)
# 手动构建⋀矩阵。对角线是特征值,顺序为eigenvalues中特征值的顺序
e = torch.Tensor([[-2, 0, 0], [0, 1, 0], [0, 0, -2]])
# 计算Q矩阵乘⋀矩阵
f = torch.mm(Q, e)
# Q⋀矩阵再乘Q的逆矩阵
g = torch.mm(f, Q_inverse)
# 输出最终结果,若其与矩阵A一致,则说明我们上述判断正确
print(g)

5. Tensor连接与切片
-
torch.cat((a,b,...),维度):将张量a,b,...按照指定维度进行拼接【二维张量中,0代表行拼接,1是列拼接,换个说法就是第0维或者第1维】可以这样理解,
维度=0,即拼接后会让a[i]中的i变多【原来只有2行,拼接完变4行】;维度=1,即拼接后会让a[i][j]中的j变多【原来只有2列,拼接完变4列】。这种理解方式在高维张量中依然通用import torch a = torch.IntTensor([[1, 1], [1, 1]]) b = torch.IntTensor([[2, 2], [2, 2]]) # a与b张量按行拼接 c = torch.cat((a, b), 0) print(c)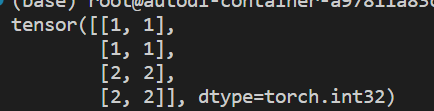
-
torch.chunk(a,parts,维度):将张量a按照指定维度均分为parts块【如果不够分则会切分大小为1的块】,可以通过下标访问不同的块# 将上述👆c行分割为2块 d = torch.chunk(c, 2, 0) # 取第1块查看【其实就是张量a】 print(d[0])
-
torch.t(a):让矩阵a转置import torch a = torch.IntTensor([[1, 2], [3, 1]]) b = torch.t(a) print(b)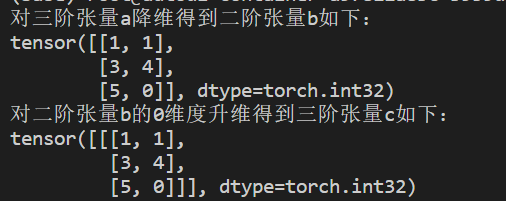
-
torch.split(a,parts,dim):将张量a按照指定维度dim划分为parts块【此时与chunk相同】,parts也可以是tuple,此时每块大小由其内数字决定,没有分配到的会整体组成一大块import torch a = torch.IntTensor([[1, 1], [1, 1]]) b = torch.IntTensor([[2, 2], [2, 2]]) # a与b张量按行拼接 c = torch.cat((a, b), 0) # 将c张量按行划分,第一块大小为3,剩下的所有行构成一块 d = torch.split(c, (3), 0) print(d)
-
torch.index_select(a,dim,index):张量a为dim维度方向按照index【类型是一阶Tensor】取对应元素import torch a = torch.IntTensor([[1, 2], [3, 4], [5, 6]]) b = torch.IntTensor([[2, 2], [2, 2]]) # 下标分别为0,2 index = torch.IntTensor([0, 2]) # 对张量a的第0维取index对应的元素,即a[0],a[2] c = torch.index_select(a, 0, index) print(c)
-
torch.unbind(a,dim):张量a按照指定维度取切片,返回值是切片的Tensor集合【通俗来说,向量的切片是标量,矩阵切片是向量,三阶张量切片是矩阵(视觉上为“一根柱子”)】
假设有三阶张量 a m × n × v 则维度 = 0 的切片表达式为: ∑ j = 0 n ∑ k = 0 v a [ i ] [ j ] [ k ] 则维度 = 1 的切片表达式为: ∑ i = 0 m ∑ k = 0 v a [ i ] [ j ] [ k ] 则维度 = 2 的切片表达式为: ∑ i = 0 m ∑ j = 0 n a [ i ] [ j ] [ k ] 假设有三阶张量a_{m\times n\times v}\\ 则维度=0的切片表达式为:\sum_{j=0}^{n}\sum_{k=0}^{v}a[i][j][k]\\ 则维度=1的切片表达式为:\sum_{i=0}^{m}\sum_{k=0}^{v}a[i][j][k]\\ 则维度=2的切片表达式为:\sum_{i=0}^{m}\sum_{j=0}^{n}a[i][j][k] 假设有三阶张量am×n×v则维度=0的切片表达式为:j=0∑nk=0∑va[i][j][k]则维度=1的切片表达式为:i=0∑mk=0∑va[i][j][k]则维度=2的切片表达式为:i=0∑mj=0∑na[i][j][k]import torch a = torch.IntTensor([[1, 2], [3, 4], [5, 6]]) # 张量a按照维度=0进行切片 c = torch.unbind(a, 0) print(c)
-
torch.nonzero(a):返回张量a内值不为0的元素索引import torch a = torch.IntTensor([[1, 2], [3, 4], [5, 0]]) c = torch.nonzero(a) print(c)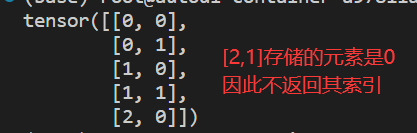
-
torch.squeeze(a):对张量降维,如果当前维度是1,就将此维度处理掉torch.unsqueeze(a,dim):对张量升维,指定在dim维度升维import torch a = torch.IntTensor([[[1, 1], [3, 4], [5, 0]]]) b = torch.squeeze(a) print('对三阶张量a降维得到二阶张量b如下:') print(b) c = torch.unsqueeze(b, 0) print('对二阶张量b的0维度升维得到三阶张量c如下:') print(c)
-
torch.transpose(a,dim1,dim2):对a张量dim1维度与dim2维度进行转置
如张量 a m × n × v , d i m 1 = 1 , d i m 2 = 2 则经过 t r a n s p o s e 操作后,张量 a 的结构变为 a m × v × m 如张量a_{m\times n\times v},dim1=1,dim2=2\\ 则经过transpose操作后,张量a的结构变为a_{m\times v\times m} 如张量am×n×v,dim1=1,dim2=2则经过transpose操作后,张量a的结构变为am×v×mimport torch a = torch.IntTensor([[[1, 1], [3, 4], [5, 0]]]) print('张量a的结构为:', a.shape) # 对张量a的0维度与1维度转置 b = torch.transpose(a, 0, 1) print('经转置后张量a的结构为:', b.shape)
6. Tensor变形
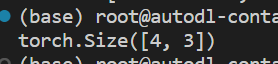
a.view(形状):将张量a改变为指定形状,当使用-1作为某一维长度时,则这一维会被自动计算
import torch
# 张量a初始形状为[2,2,3]
a = torch.IntTensor(2, 2, 3)
# 将张量a的形状改变为[4,3]
b = a.view(4, 3)
print(b.shape)
7. Tensor自动微分
Pytorch的Autograd技术可以帮助我们自动求微分值
7.1 微分实例


7.2 基本原理
复杂的计算可以被抽象成一张图,一张复杂的计算图可以分成4个部分:
- 叶子节点【图的末端,没有信息流经过,但信息流由此出发】
- 中间节点【有信息流经过,信息流经过中间节点来到末端输出叶子节点】
- 输出节点
- 信息流【可以理解为有用信息集合,如上述求关于 x 1 x_1 x1 的微分,此时 x 1 x_1 x1 就说有用的信息】
微分示例中的
x
→
\overrightarrow{x}
x 是叶子节点、
z
→
\overrightarrow{z}
z 是中间节点、
y
→
\overrightarrow{y}
y 是输出节点,三者都是Tensor
Tensor在自动微分方面有三个重要属性👇:
requires_grad:布尔值,默认为False,为True时表示此张量需要自动微分grad:存储张量微分值grad_fn:存储张量微分函数
当叶子节点的requires_grad为True,信息流经过该节点时,所有中间节点的requires_grad属性都会变为True,只要在输出节点调用反向传播函数backward(),Pytorch就会自动求出叶子节点的微分值并更新存储在叶子节点的grad属性中。
需要注意的是:只有叶子节点的grad属性能被更新
7.3 代码示例
import torch
# x是一维张量且值全为 1
x = torch.ones(2)
print('反向传播前,x的grad属性值:', x.grad)
# 我们后边需要计算 y 关于 x 的微分,因此 x 的 requires_grad 属性设置为 True
x.requires_grad = True
# 张量 x 的每个元素都乘 4 得到张量 z
z = x*4
# y 的值等于 z 的二阶范数
# 所谓二阶范数就是 张量内所有元素平方和再开方,与上述微分例子中一致
y = z.norm()
# y 启动反向传播,执行完毕后就能得到 y 关于张量 x 的微分【存储在 x 的 grad 中】
y.backward()
print('反向传播后,x的grad属性值:', x.grad)

