代码随想录Day44
今天继续学习通过动态规划解决问题
96.不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
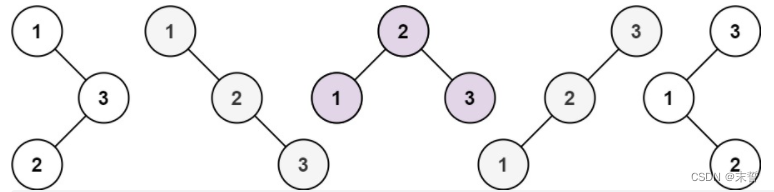
输入:n = 3
输出:5
思路:
1.首先想dp数组的含义,用i表示i个结点,dp[i]则是由i个结点组成的互不相同的二叉搜索树个数。
2.关于初始化的问题,dp[0]实际上对应的就是0个结点的空二叉树,而空二叉树实际上也是可以算作一种二叉搜索树的,因此将dp[0]初始化为1。(如果将dp[0]初始化为0,dp[1]通过计算也会得到0,在这之后的所有递推也都只会是0)。
2.确定了dp数组的含义后,可以想象得到肯定i需要从1遍历到n,那么我们就用题目示例中给出的2和3再加上1来举例子。可以看出无论i等于多少,其所对应的结果都是根结点为1,根结点为2,根节点为3......根节点为i的所有二叉搜索树个数全部加起来。因此在确定i后我们还需要进行一层遍历,遍历从1到i作为根节点的所有二叉搜索树并将其加起来就是dp[i]。
3.当确定了根节点为j后,我们就可以通过二叉搜索树的特性确定其左右子树的结点个数,左子树结点一定为j - 1,右子树结点个数一定为i - j(如果实在想不出,举几个例子即可发现规律),且其左右子树也同样是二叉搜索树,对应着dp[j - 1]和dp[i - j]。
因此我们可以得出递推公式:dp[i] += dp[j - 1] * dp[i - j]。
4.最后关于递归顺序,由递推公式可以看出dp[i]需要由之前已经计算出的dp[j - 1]和dp[i - j]得到,且j - 1和i - j一定比i小,所以遍历顺序是从前往后。
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;//空二叉树也是一种二叉搜索树
//通过i遍历从1到n的互不相同的二叉搜索树
//j来遍历对应i时,j作为头结点的二叉搜索树个数
//此时左子树中共有j - 1个头结点,右子树中共有i - j个头结点,而左右子树也一样是二叉搜索树
for(int i = 1; i <= n; i++){
for(int j = 1; j <= i; j++){
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};启发:
1.本题尽管代码简短,但其中蕴含的思路细节却并不算简单,尤其是如何找到递推公式是一大难点。其实从题目中给的那一个示例图不难看出,n个结点实际上对应的就是将1-n作为根节点的所有二叉搜索树的情况。同时也别忘了二叉搜索树中根节点的左右子树也同样是二叉搜索树,因此其左右子树中实际上也满足是拥有x个结点的二叉搜索树,可以通过递推公式在之前求得。
