如何用Python求解微分方程组

odeint简介

scipy文档中将odeint函数和ode, comples_ode这两个类称为旧API，是scipy早期使用的微分方程求解器，但由于是Fortran实现的，尽管使用起来并不方便，但速度没得说，所以有的时候还挺推荐使用的。

其中，odeint的参数如下

scipy.integrate.odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0, tfirst=False)

其中func为待求解函数；y0为初值；t为自变量列表，其他参数都有默认选项，可以不填，而且这些参数非常多，其中常用的有

• args func中除了t之外的其他变量
• Dfun func的梯度函数，当此参数不为None时，若将col_deriv设为True，则可提升效率。
• full_output 如果为True，则额外返回一个参数字典
• ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5,
• printmessg 为True时打印信息。
• tfirst 当为False时，func的格式为func(y,t...)，否则格式为func(t, y...)

示例

对于常微分方程

$$\begin{gathered} {\theta }^{\prime \prime }(t)+b{\theta }^{\prime }(t)+c\sin \theta (t)=0 \\ b=0.25;c=5 \\ \theta (0)=\pi -0.1;{\theta }^{\prime }(0)=0 \end{gathered}$$

将其中的二阶导数项用一个新变量替代，$\omega (t)={\theta }^{\prime }(t)$，则常微分方程可拆分成微分方程组

$$\begin{array}{rl}{\theta }^{\prime }(t)& =\omega (t)\\ {\omega }^{\prime }(t)& =-b\omega (t)-c\sin \theta (t)\end{array}$$

令$y=[\theta ,\omega ]$，则$y^{\prime }=[{\theta }^{\prime },{\omega }^{\prime }]$，据此可设计函数func

import numpy as np
def pend(y, t, b, c):
    th, om = y
    dydt = [om, -b*om - c*np.sin(th)]
    return dydt

然后调用并求解

from scipy.integrate import odeint
y0 = [np.pi-0.1, 0]
t = np.linspace(0, 10, 101)
sol = odeint(pend, y0, t, args=(0.25, 5))

然后绘制一下结果

import matplotlib.pyplot as plt
plt.plot(t, sol[:,0], label="theta")
plt.plot(t, sol[:,1], label="omega")
plt.legend()
plt.show()

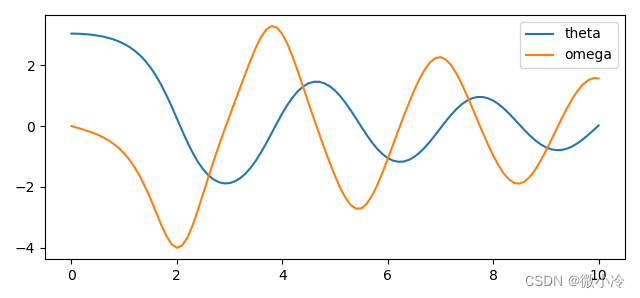
这个形状还是比较离奇的。