全连接神经网络
目录
1.全连接神经网络简介
2.MLP分类模型
2.1 数据准备与探索
2.2 搭建网络并可视化
2.3 使用未预处理的数据训练模型
2.4 使用预处理后的数据进行模型训练
3. MLP回归模型
3.1 数据准备
3.2 搭建回归预测网络
1.全连接神经网络简介
全连接神经网络(Multi-Layer Perception,MLP)或者叫多层感知机,是一种连接方式较为简单的人工神经网络结构,属于前馈神经网络的一种,主要由输入层、隐藏层和输出层构成,并且在每个隐藏层中可以有多个神经元。MLP网络是可以应用于几乎所有任务的多功能学习方法,包括分类、回归,甚至是无监督学习。
神经网络的学习能力主要来源于网络结构,而且根据层的数量不同、每层神经元数量的多少,以及信息在层之间的传播方式,可以组合成多种神经网络模型。全连接神经网络主要由输入层、隐藏层和输出层构成。输入层仅接收外界的输人,不进行任何函数处理,所以输入层的神经元个数往往和输入的特征数量相同,隐藏层和输出层神经元对信号进行加工处理,最终结果由输出层神经元输出。根据隐藏层的数量可以分为单隐藏层MLP和多隐藏层MLP,它们的网络拓扑结构如下图所示:
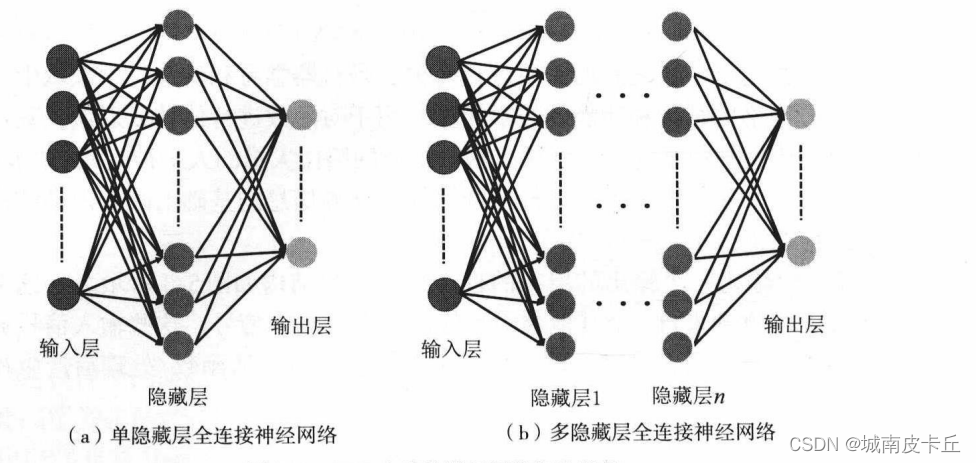
2.MLP分类模型
2.1 数据准备与探索
下面使用PyTorch中的相关模块搭建多隐藏层的全连接神经网络,并使用不同的真实数据集,用于探索MLP在分类和回归任务中的应用。
首先我们来使用MLP探索其在分类任务中的应用。数据集我们使用垃圾邮件数据集Spambase,
数据集下载地址为:Index of /ml/machine-learning-databases/spambase![]() https://archive.ics.uci.edu/ml/machine-learning-databases/spambase/
https://archive.ics.uci.edu/ml/machine-learning-databases/spambase/
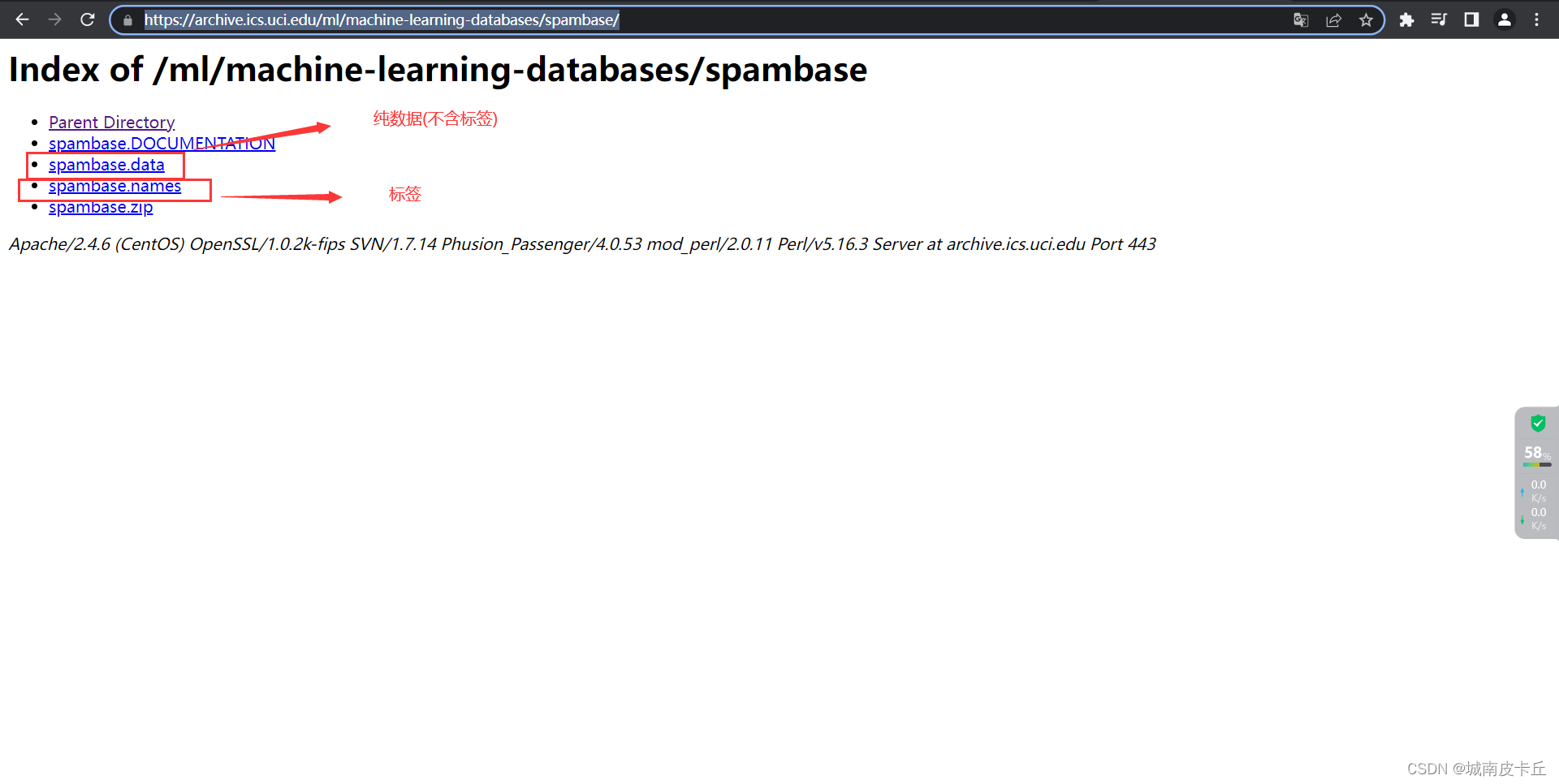
值得注意的是,从该网址下载的数据集需要经过一定的手工处理才能被我们后续使用。具体来说
- spambase.data
 https://archive.ics.uci.edu/ml/machine-learning-databases/spambase/spambase.data
https://archive.ics.uci.edu/ml/machine-learning-databases/spambase/spambase.data
该文件是二进制文件,下载后我们直接将文件后缀名更改为.csv,并且由于该文件是纯数据,不含列名(即没有数据标签),我们需要额外下载
- spambase.names
 https://archive.ics.uci.edu/ml/machine-learning-databases/spambase/spambase.names
https://archive.ics.uci.edu/ml/machine-learning-databases/spambase/spambase.names
该文件是数据标签,不含数据。下载后需要将该文件中的56个标签添加为spambase.csv的列名才能为后续所用。
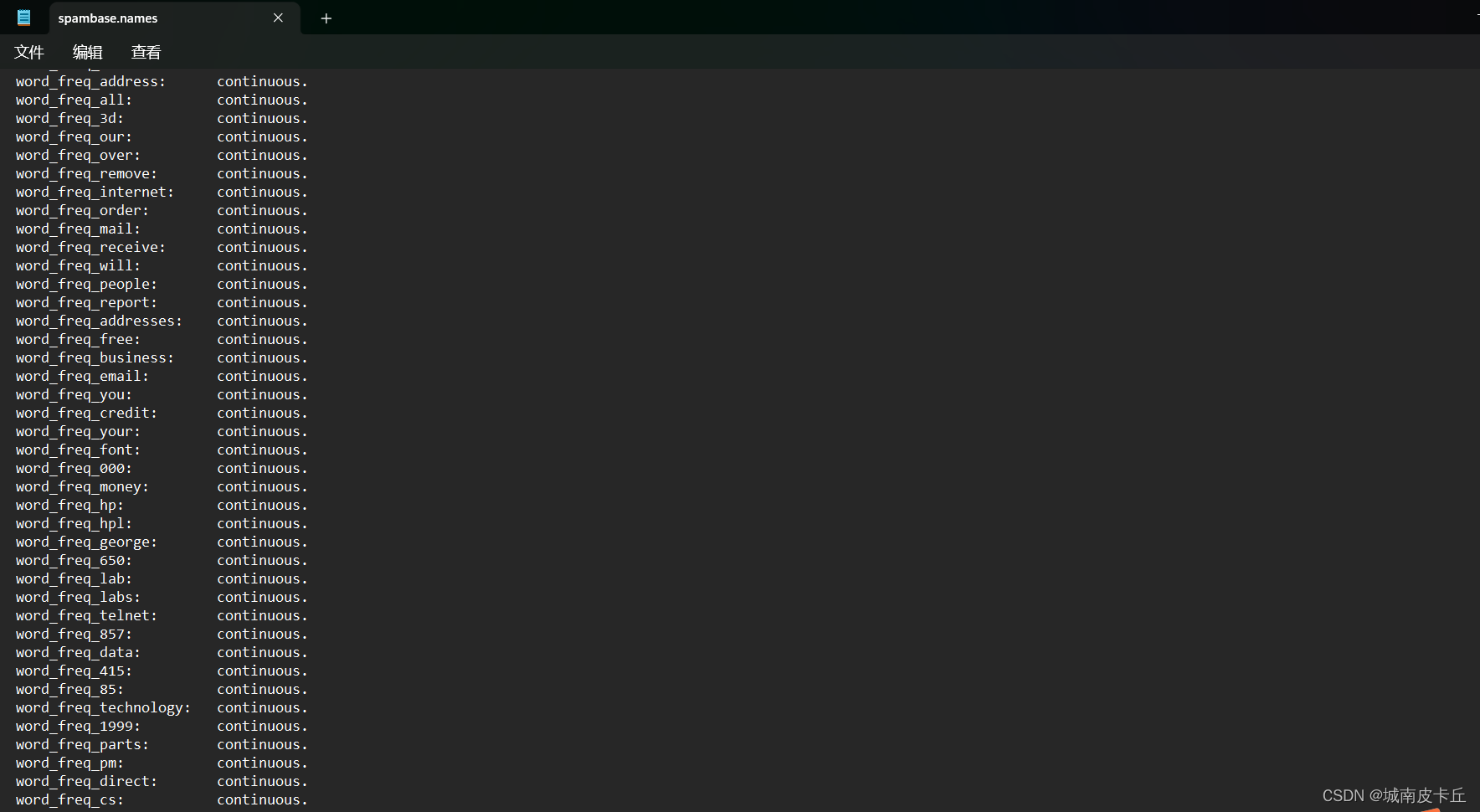

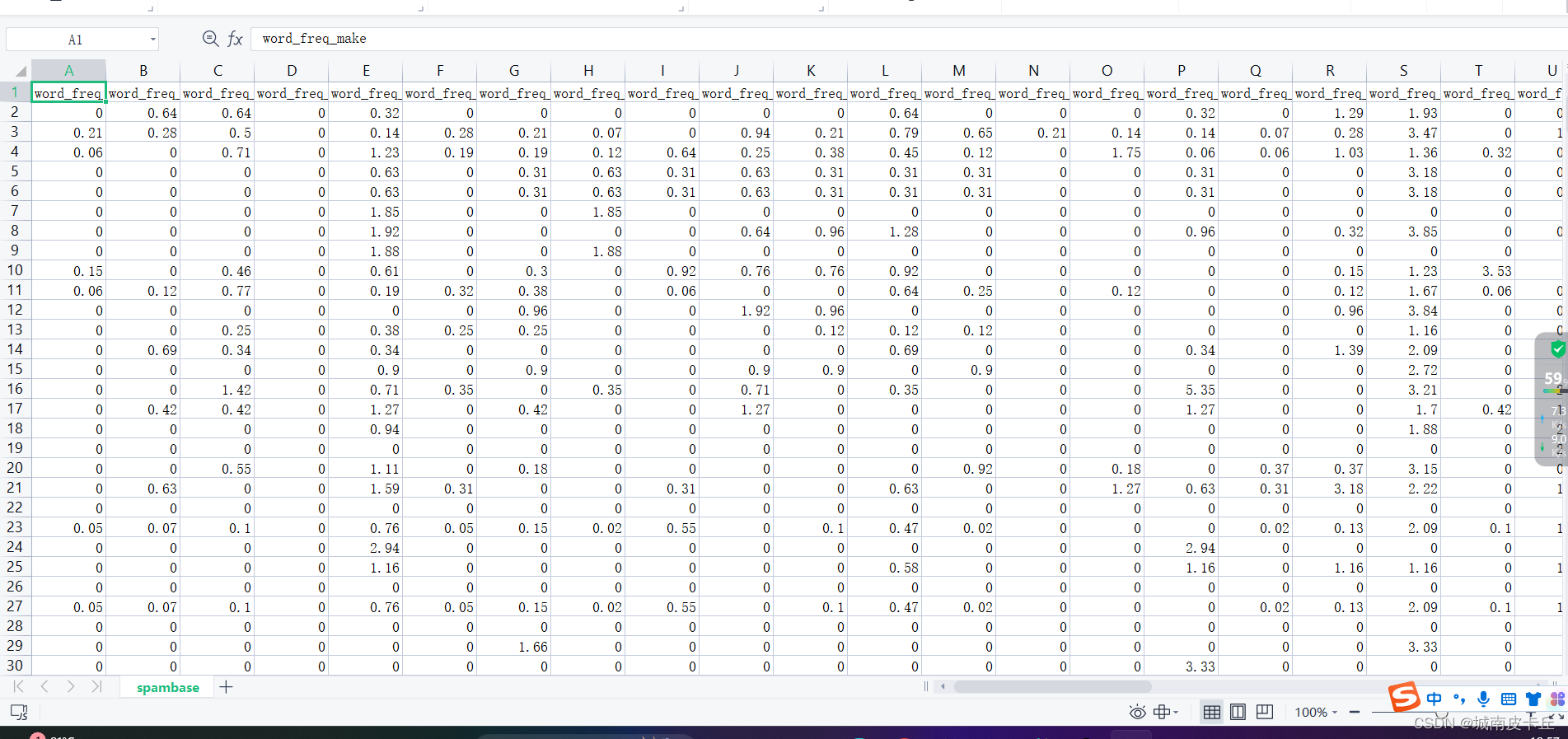
在该数据集中,包含57个邮件内容的统计特征,其中有48个特征是关键词出现的频率×100的取值,范围为[0,100 ],变量名使用word_freq_WORD命名,WORD表示该特征统计的词语;6个特征为关键字符出现的频率x100取值,范围为[0,100 ],变量名使用char_freq_CHAR命名;1个变量为capital_run_length_average,表示大写字母不间断的平均长度;1个变量为capital_run_length_longest,表示大写字母不间断的最大长度;1个变量capital_run_length_total表示邮件中大写字母的数量。数据集中最后一个变量是待预测目标变量(0、1),表示电子邮件被认为是垃圾邮件(1)或不是(0)。
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from torch.optim import SGD,Adam
import torch.utils.data as Data
import matplotlib.pyplot as plt
import seaborn as sns
import hiddenlayer as hl
from torchviz import make_dot
from sklearn.preprocessing import StandardScaler,MinMaxScaler#用于数据标准化预处理
from sklearn.model_selection import train_test_split#用于数据集的切分
from sklearn.metrics import accuracy_score,confusion_matrix,classification_report#用于评价模型预测效果
from sklearn.manifold import TSNE#用于数据的降维及可视化
spam=pd.read_csv("../Dataset/spambase.csv")
print(spam.head())
print(pd.value_counts(spam.label))
"""
发现数据集中垃圾邮件有1813个样本,非垃圾邮件有2788个样本。
为了验证训练好的MLP网络的性能,需要将数据集spam切分为训练集和测试集,
其中使用75%的数据作为训练集,剩余25%的数据作为测试集,以测试训练好的模型的泛化能力。
数据集切分可以使用train_test_split()函数:
"""
#将数据集随机切分成训练集和测试集
X=spam.iloc[:,0:57].values
y=spam.label.values
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=123)
"""
切分好数据后,需要对数据进行标准化处理。此处采用MinMaxScaler()将数据进行最大值-最小值标准化,
将数据集中的每个特征取值范围转化到0 ~ 1之间,程序如下:
"""
#对前57列特征数据进行标准化处理
scales=MinMaxScaler(feature_range=(0,1))
X_train_s=scales.fit_transform(X_train)
X_test_s=scales.transform(X_test)
"""
在得到标准化数据后,将训练数据集的每个特征变量使用箱线图进行显示,
对比不同类别的邮件(垃圾邮件和非垃圾邮件)在每个特征变量上的数据分布情况。
"""
colname=spam.columns.values[:-1]
plt.figure(figsize=(20,8))
for i in range(len(colname)):
plt.subplot(7,9,i+1)
sns.boxplot(x=y_train,y=X_train_s[:,i])
plt.title(colname[i])
plt.subplots_adjust(hspace=0.4)
plt.show()
使用sns.boxplot()函数将数据集X_train_s中的57个特征变量进行了可视化,得到的图像如下图所示:
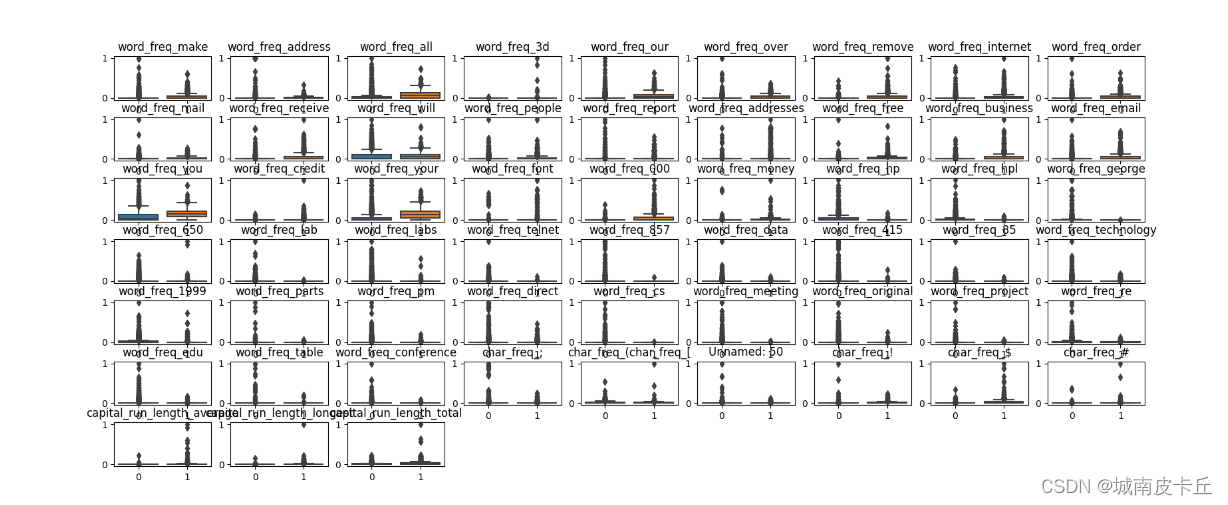
2.2 搭建网络并可视化
在数据准备、探索和可视化分析之后,下面搭建需要使用的全连接神经网络分类器。
class MLPclassify(nn.Module):
def __init__(self):
super(MLPclassify,self).__init__()
#定义第一个隐藏层
self.hidden1=nn.Sequential(
nn.Linear(
in_features=57,#第一个隐藏层的输入,数据的特征数
out_features=30,#第一个隐藏层的输出,神经元的数量
bias=True
),
nn.ReLU()
)
#定义第二个隐藏层
self.hidden2=nn.Sequential(
nn.Linear(30,10),
nn.ReLU()
)
#分类层
self.classify=nn.Sequential(
nn.Linear(10,2),
nn.Sigmoid()
)
#定义网络的前向传播
def forward(self,x):
fc1=self.hidden1(x)
fc2=self.hidden2(fc1)
output=self.classify(fc2)
#输出为两个隐藏层和两个输入层
return fc1,fc2,output
"""
上面的程序中定义了一个MLPclassify函数类,其网络结构中含有hidden1和hidden2两个隐藏层,
分别包含30和10个神经元以及1个分类层classify,并且分类层使用Sigmoid函数作为激活函数。
由于数据有57个特征,所以第一个隐藏层的输入特征为57,而且该数据为二分类问题,所以分类层有2个神经元。
在定义完网络结构后,需要定义网络的正向传播过程,
分别输出了网络的两个隐藏层fc1、fc2以及分类层的输出output。
"""
mlp=MLPclassify()
x=torch.randn(1,57).requires_grad_(True)
y=mlp(x)
myMlp=make_dot(y,params=dict(list(mlp.named_parameters())+[('x',x)]))
myMlp.format='png'#指定可视化图像的格式
myMlp.directory="model_graph/"#指定图像保存的文件夹
myMlp.view()
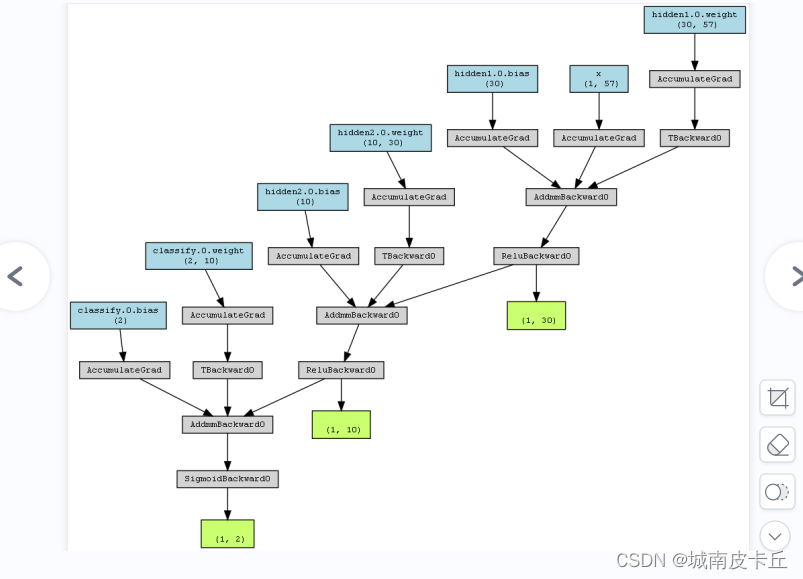
2.3 使用未预处理的数据训练模型
在网络搭建完毕后,首先使用未标准化的训练数据训练模型,然后利用未标准化的测试数据验证模型的泛化能力,分析网络在未标准化的数据集中是否也能很好地拟合数据。首先将未标准化的数据转化为张量,并且将张量处理为数据加载器:
#将数据转化为张量
X_train_nots=torch.from_numpy(X_train.astype(np.float32))
y_train_t=torch.from_numpy(y_train.astype(np.int64))
X_test_nots=torch.from_numpy(X_test.astype(np.float32))
y_test_t=torch.from_numpy(y_test.astype(np.int64))
#将训练集转化为张量之后,使用TensorDataset将X与Y整理到一起
train_data_nots=Data.TensorDataset(X_train_nots,y_train_t)
#定义一个数据加载器对训练数据集进行批量处理
train_nots_loader=Data.DataLoader(
dataset=train_data_nots,#使用的数据集
batch_size=64,#批处理样本大小
shuffle=True,#每次迭代前打乱数据
num_workers=0
)
#定义优化器
optimizer=torch.optim.Adam(mlp.parameters(),lr=0.01)
loss_func=nn.CrossEntropyLoss()#二分类损失函数
#记录训练过程的指标
history1=hl.History()
#使用Canvas进行可视化
canvas1=hl.Canvas()
print_step=25
#对模型进行迭代训练,对所有数据训练epoch轮
for epoch in range(30):
# 对训练数据的加载器进行迭代训练
for step,(b_x,b_y) in enumerate(train_nots_loader):
#计算每个batch的损失
_,_,output=mlp(b_x)#MLP在训练batch上的输出
train_loss=loss_func(output,b_y)#二分类交叉熵损失函数
optimizer.zero_grad()#每个迭代步的梯度初始化为0
train_loss.backward()#损失后向传播,计算梯度
optimizer.step()#使用梯度进行优化
nither=epoch*len(train_nots_loader)+step+1
#计算每经过print_step次迭代后的输出
if nither % print_step ==0:
_,_,output=mlp(X_test_nots)
_,pre_lab=torch.max(output,1)
test_accuray=accuracy_score(y_test_t,pre_lab)
#为history添加epoch,损失和精度
history1.log(nither,train_loss=train_loss,test_accuray=test_accuray)
##使用两个图像可视化损失函数和精度
print(train_loss)
print(test_accuray)
with canvas1:
canvas1.draw_plot(history1["train_loss"])
canvas1.draw_plot(history1["test_accuray"])
"""
上面的程序对训练数据集进行了5个epoch的训练,在网络训练过程中,
每经过25次迭代就对测试集进行一次预测,并且将迭代次数、
训练集上损失函数的取值、模型在测试集上的识别精度都
使用history1.log()函数进行保存,再使用canvas1.draw_plot()函数
将损失函数大小、预测精度实时可视化出来。
"""从Hiddenlayer可视化结果可以看出,损失函数一直在波动,并没有收敛到一个平稳的数值区间,在测试集上的精度也具有较大的波动范围,而且最大精度低于72%。说明使用未标准化的数据集训练的模型并没有训练效果,即MLP分类器没有收敛。
导致这样结果的原因可能较多,例如:
(1)数据没有经过标准化预处理,所以网络没有收敛。(2)使用的训练数据样本太少,导致网络没有收敛。(3)搭建的MLP网络使用的神经元太多或者太少,所以网络没有收敛。
2.4 使用预处理后的数据进行模型训练
MLP分类器没有收敛的原因可以有多个,但是最可能的原因是数据没有进行标准化预处理。为了验证猜想的正确性,使用标准化数据集重新对上面的MLP网络进行训练,观察训练集和测试集在网络训练过程中的表现,查看网络是否收敛。
import numpy as np
import pandas as pd
import torch
import torch.nn as nn
from torch.optim import SGD,Adam
import torch.utils.data as Data
import matplotlib.pyplot as plt
import seaborn as sns
# import hiddenlayerDemo as hl
import hiddenlayer as hl
from torchviz import make_dot
from sklearn.preprocessing import StandardScaler,MinMaxScaler#用于数据标准化预处理
from sklearn.model_selection import train_test_split#用于数据集的切分
from sklearn.metrics import accuracy_score,confusion_matrix,classification_report#用于评价模型预测效果
from sklearn.manifold import TSNE#用于数据的降维及可视化
spam=pd.read_csv("../Dataset/spambase.csv")
#将数据集随机切分成训练集和测试集
X=spam.iloc[:,0:57].values
y=spam.label.values
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=123)
# """
# 切分好数据后,需要对数据进行标准化处理。此处采用MinMaxScaler()将数据进行最大值-最小值标准化,
# 将数据集中的每个特征取值范围转化到0 ~ 1之间,程序如下:
# """
#对前57列特征数据进行标准化处理
scales=MinMaxScaler(feature_range=(0,1))
X_train_s=scales.fit_transform(X_train)
X_test_s=scales.transform(X_test)
class MLPclassify(nn.Module):
def __init__(self):
super(MLPclassify,self).__init__()
#定义第一个隐藏层
self.hidden1=nn.Sequential(
nn.Linear(
in_features=57,#第一个隐藏层的输入,数据的特征数
out_features=30,#第一个隐藏层的输出,神经元的数量
bias=True
),
nn.ReLU()
)
#定义第二个隐藏层
self.hidden2=nn.Sequential(
nn.Linear(30,10),
nn.ReLU()
)
#分类层
self.classify=nn.Sequential(
nn.Linear(10,2),
nn.Sigmoid()
)
#定义网络的前向传播
def forward(self,x):
fc1=self.hidden1(x)
fc2=self.hidden2(fc1)
output=self.classify(fc2)
#输出为两个隐藏层和两个输入层
return fc1,fc2,output
mlp=MLPclassify()
#将数据转化为张量
X_train_nots=torch.from_numpy(X_train_s.astype(np.float32))
y_train_t=torch.from_numpy(y_train.astype(np.int64))
X_test_nots=torch.from_numpy(X_test_s.astype(np.float32))
y_test_t=torch.from_numpy(y_test.astype(np.int64))
#将训练集转化为张量之后,使用TensorDataset将X与Y整理到一起
train_data_nots=Data.TensorDataset(X_train_nots,y_train_t)
#定义一个数据加载器对训练数据集进行批量处理
train_nots_loader=Data.DataLoader(
dataset=train_data_nots,#使用的数据集
batch_size=64,#批处理样本大小
shuffle=True,#每次迭代前打乱数据
num_workers=0
)
#定义优化器
optimizer=torch.optim.Adam(mlp.parameters(),lr=0.01)
loss_func=nn.CrossEntropyLoss()#二分类损失函数
#记录训练过程的指标
history1=hl.History()
#使用Canvas进行可视化
canvas1=hl.Canvas()
print_step=25
#对模型进行迭代训练,对所有数据训练epoch轮
for epoch in range(30):
# 对训练数据的加载器进行迭代训练
for step,(b_x,b_y) in enumerate(train_nots_loader):
#计算每个batch的损失
_,_,output=mlp(b_x)#MLP在训练batch上的输出
train_loss=loss_func(output,b_y)#二分类交叉熵损失函数
optimizer.zero_grad()#每个迭代步的梯度初始化为0
train_loss.backward()#损失后向传播,计算梯度
optimizer.step()#使用梯度进行优化
nither=epoch*len(train_nots_loader)+step+1
#计算每经过print_step次迭代后的输出
if nither % print_step ==0:
_,_,output=mlp(X_test_nots)
_,pre_lab=torch.max(output,1)
test_accuray=accuracy_score(y_test_t,pre_lab)
#为history添加epoch,损失和精度
history1.log(nither,train_loss=train_loss,test_accuray=test_accuray)
##使用两个图像可视化损失函数和精度
print(train_loss)
print(test_accuray)
with canvas1:
canvas1.draw_plot(history1["train_loss"])
canvas1.draw_plot(history1["test_accuray"])
从上面Hiddenlayer可视化图像可以看出损失函数最终收敛到一个平稳的数值区间,在测试集上的精度也得到了收敛,预测精度稳定在90%以上。说明模型在使用标准化数据后得到有效的训练。即数据标准化预处理对MLP网络非常重要。
3. MLP回归模型
在sklearn库中,包含一个fetch_california_housing(函数,该函数可以下载california房屋价格数据。该数据集源自1990年美国人口普查,每行样本是每个人口普查区块组的描述数据,区块组通常拥有600~3000的人口。在数据集中一共包含20640个样本,数据有8个自变量,如收入平均数、房屋年龄、平均房间数量等。因变量为房屋在该区块组的价格中位数。使用该数据集建立一个全连接回归模型,用于预测房屋的价格。
3.1 数据准备
import numpy as np
import pandas as pd
import sklearn.datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,mean_absolute_error
from sklearn.datasets import fetch_california_housing
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import SGD
import torch.utils.data as Data
import matplotlib.pyplot as plt
import seaborn as sns
#导入数据
print(sklearn.datasets.get_data_home())
house_data=fetch_california_housing()
#将数据切分成训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(
house_data.data,
house_data.target,
test_size=0.3,
random_state=42)
#数据标准化处理
scale=StandardScaler()
X_train_s=scale.fit_transform(X_train)
X_test_s=scale.transform(X_test)
#将训练集数据处理为数据表,方便探索数据情况
house_data_df=pd.DataFrame(data=X_train_s,columns=house_data.feature_names)
house_data_df["target"]=y_train
"""
在上面的程序中,首先通过fetch_california_housing()函数导入数据,
然后通过train_test_split()函数将数据集的70%作为训练集,30%作为测试集,
并通过StandardScaler()函数类对数据进行标准化,
最后使用pd.DataFrame()函数将标准化的训练数据集处理为数据表
"""
#可视化数据的相关系数热力图
data_cor=np.corrcoef(house_data_df.values,rowvar=0)
data_cor=pd.DataFrame(data=data_cor,columns=house_data_df.columns,index=house_data_df.columns)
plt.figure(figsize=(8,6))
ax=sns.heatmap(data_cor,square=True,annot=True,fmt=".3f",
linewidths=.5,
cmap="YlGnBu",
cbar_kws={"fraction":0.046,"pad":0.03})
plt.show()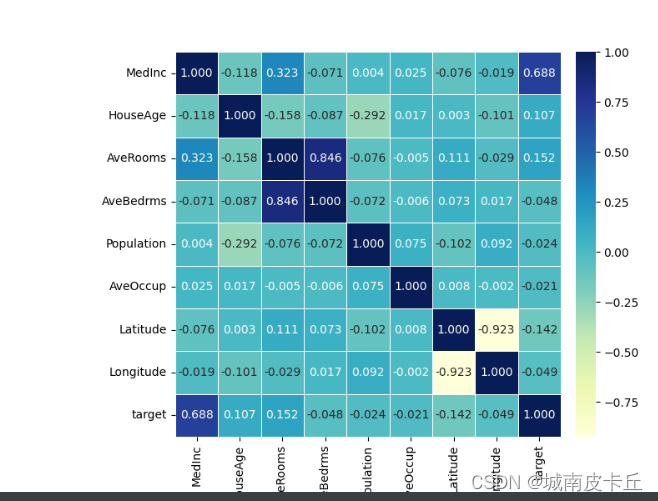
上面的程序通过函数np.corrcoef()计算变量之间的相关系数,然后通过sns.heatmap()可视化相关系数热力图,得到如上图所示的图像。 从图像中可以发现和目标函数相关性最大的是MedInc(收入中位数)变量。而且AveRooms和AveBedrms两个变量之间的正相关性较强。
3.2 搭建回归预测网络
用准备好的数据通过PyTorch构建一个全连接神经网络的类,搭建MLP回归模型。
import numpy as np
import pandas as pd
import sklearn.datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error,mean_absolute_error
from sklearn.datasets import fetch_california_housing
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import SGD
import torch.utils.data as Data
import matplotlib.pyplot as plt
import seaborn as sns
#导入数据
house_data=fetch_california_housing()
#将数据切分成训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(
house_data.data,
house_data.target,
test_size=0.3,
random_state=42)
#数据标准化处理
scale=StandardScaler()
X_train_s=scale.fit_transform(X_train)
X_test_s=scale.transform(X_test)
#将数据集转化为张量
train_xt=torch.from_numpy(X_train_s.astype(np.float32))
train_yt=torch.from_numpy(y_train.astype(np.float32))
test_xt=torch.from_numpy(X_test_s.astype(np.float32))
test_yt=torch.from_numpy(y_test.astype(np.float32))
#将训练数据处理为数据加载器
train_data=Data.TensorDataset(train_xt,train_yt)
test_data=Data.TensorDataset(test_xt,test_yt)
train_loader=Data.DataLoader(dataset=train_data,batch_size=64,shuffle=True,num_workers=0)
"""搭建全连接神经网络回归模型"""
class MLPregression(nn.Module):
def __init__(self):
super(MLPregression,self).__init__()
#定义第一个隐藏层
self.hidden1=nn.Linear(in_features=8,out_features=100,bias=True)
#定义第二个隐藏层
self.hidden2=nn.Linear(100,100)
#定义第三个隐藏层
self.hidden3=nn.Linear(100,50)
#回归预测层
self.predict=nn.Linear(50,1)
def forward(self,x):
x=F.relu(self.hidden1(x))
x=F.relu(self.hidden2(x))
x=F.relu(self.hidden3(x))
output=self.predict(x)
#返回一个一维向量
return output[:,0]
mlp=MLPregression()
"""使用训练集对网络进行训练"""
optimizer=torch.optim.SGD(mlp.parameters(),lr=0.01)
loss_func=nn.MSELoss()#均方根误差损失函数
train_loss_all=[]
#对模型进行迭代训练,对所有的数据训练epoch轮
for epoch in range(30):
train_loss=0
train_num=0
#对训练数据的加载器进行迭代计算
for step,(b_x,b_y) in enumerate(train_loader):
output=mlp(b_x)#mlp在训练batch上的输出
loss=loss_func(output,b_y)#均方根误差损失函数
optimizer.zero_grad()#每个迭代步的梯度初始化为0
loss.backward()#损失的后向传播,计算梯度
optimizer.step()#使用梯度进行优化
train_loss +=loss.item() * b_x.size(0)
train_num +=b_x.size(0)
train_loss_all.append(train_loss / train_num)
"""可视化损失函数变化情况"""
plt.figure(figsize=(10,6))
plt.plot(train_loss_all,"ro-",label="Train loss")
plt.legend()
plt.grid()
plt.xlabel("epoch")
plt.ylabel("Loss")
plt.show()
上述程序得到如下可视化图像:
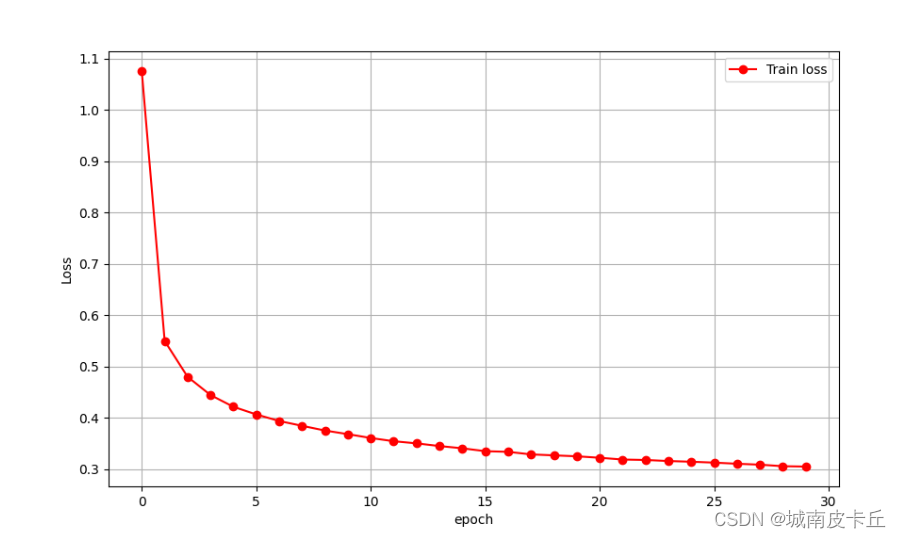
对网络进行预测,并使用平均绝对值误差来表示预测效果,程序如下所示:
"""对测试集进行预测"""
pre_y=mlp(test_xt)
pre_y=pre_y.data.numpy()
mae=mean_absolute_error(y_test,pre_y)
#将测试集上的真实值和预测值进行可视化,查看它们之间的差异
index=np.argsort(y_test)
plt.figure(figsize=(12,5))
plt.plot(np.arange(len(y_test)),y_test[index],"r",label="Original Y")
plt.scatter(np.arange(len(pre_y)),pre_y[index],s=3,c="b",label="Prediction")
plt.legend(loc="upper left")
plt.grid()
plt.xlabel("Index")
plt.ylabel("Y")
plt.show()
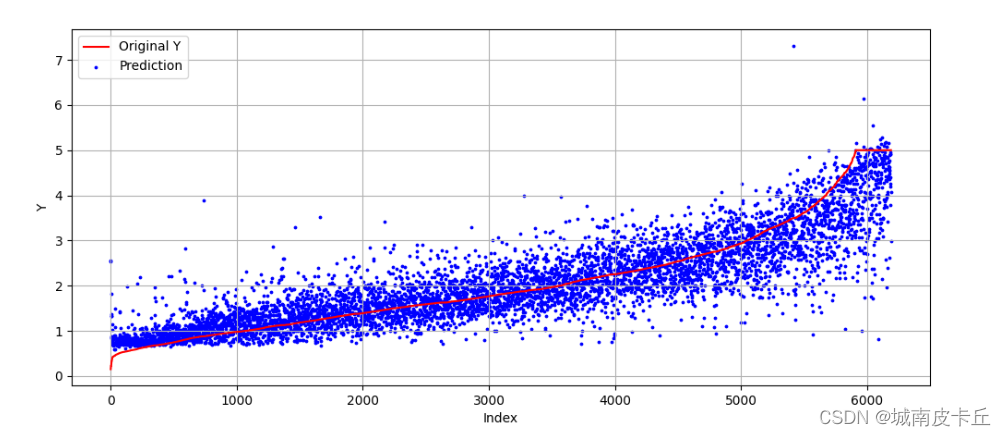 在测试集上,MLP回归模型正确地预测出了原始数据的变化趋势,但部分样本的预测差异较大。
在测试集上,MLP回归模型正确地预测出了原始数据的变化趋势,但部分样本的预测差异较大。
