蓝桥杯第十四届省赛完整题解 C/C++ B组
没有测评,不知道对不对,仅仅过样例而已
试题 A: 日期统计
本题总分:5 分
【问题描述】
小蓝现在有一个长度为 100 的数组,数组中的每个元素的值都在 0 到 9 的 范围之内。数组中的元素从左至右如下所示:
5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2 7 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 3 8 5 1 6 3 4 6 7 0 7 8 2 7 6 8 9 5 6 5 6 1 4 0 1 0 0 9 4 8 0 9 1 2 8 5 0 2 5 3 3
现在他想要从这个数组中寻找一些满足以下条件的子序列:
1. 子序列的长度为 8;
2. 这个子序列可以按照下标顺序组成一个 yyyymmdd 格式的日期,并且 要求这个日期是 2023 年中的某一天的日期,例如 20230902,20231223。 yyyy 表示年份,mm 表示月份,dd 表示天数,当月份或者天数的长度只 有一位时需要一个前导零补充。 请你帮小蓝计算下按上述条件一共能找到多少个不同 的 2023 年的日期。 对于相同的日期你只需要统计一次即可。
【答案提交】 235
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
办法比较笨,但是思路极其简单,别看有八层循环了,前4层接近没有,效率也挺高

#include<bits/stdc++.h>
#define LL long long
using namespace std;
bool date_flag[1232]; //月+日 的范围是 01-01 到 12-31 ,找到哪个日期,就标记为 true;
int main(){
int A[]={5, 6, 8, 6, 9, 1, 6, 1, 2, 4, 9, 1, 9, 8, 2, 3, 6, 4, 7, 7, 5, 9, 5, 0, 3, 8, 7, 5, 8, 1, 5, 8, 6, 1, 8, 3, 0, 3, 7, 9, 2,
7, 0, 5, 8, 8, 5, 7, 0, 9, 9, 1, 9, 4, 4, 6, 8, 6, 3, 3, 8, 5, 1, 6, 3, 4, 6, 7, 0, 7, 8, 2, 7, 6, 8, 9, 5, 6, 5, 6, 1, 4, 0, 1,
0, 0, 9, 4, 8, 0, 9, 1, 2, 8, 5, 0, 2, 5, 3, 3};
for(int a=0; a<=100-8; a++){ //2
if(A[a]!=2)continue;
for(int b=a+1; b<=100-7; b++){ //0
if(A[b]!=0)continue;
for(int c=b+1; c<=100-6; c++){ //2
if(A[c]!=2)continue;
for(int d=c+1; d<=100-5; d++){ //3
if(A[d]!=3)continue;
for(int e=d+1; e<=100-4; e++){ //月份第一个数
if(A[e]>1)continue;
for(int f=e+1; f<=100-3; f++){ //月第二个数
int month=A[e]*10+A[f]; //月份
if(month>12 || month==0)continue;
for(int g=f+1; g<=100-2; g++){//日第一个数
if(A[g]>3)continue;
for(int h=g+1; h<=100-1; h++){//日第二数
int day=A[g]*10+A[h]; // 日
if(day>31 || day==0)continue; //需要注意日期合法性, 比如:2月31日就不合法
int i = month*100+day;
// printf("2023 %04d\n",i); //可以输出看一下
date_flag[i]=true;
} } } } } } } }
int ans=0,uu=0;
for(int i=101; i<1231; i++){
if(i==229 || i==230 || i==231 || i==431 || i==631 || i==931 || i==1131 ) //不合法日期 (2023年不是润年)
continue;
ans+=date_flag[i];
}
cout<<ans;
return 0;
}
试题 B: 01 串的熵
本题总分:5 分
【问题描述】
对于一个长度为 n 的 01 串 S = x1 x2 x3...xn,香农信息熵的定义为 H(S ) = −Σ n 1 p(xi)log2 (p(xi)),其中 p(0), p(1) 表示在这个 01 串中 0 和 1 出现的占比。 比如,对于 S = 100 来说,信息熵 H(S ) = − 1/3 log2 ( 1/3 ) – 2/3 log2( 2/3 ) – 2/3 log2 ( 2/3 ) = 1.3083。对于一个长度为 23333333 的 01 串,如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少,那么这个 01 串中 0 出现了多少次?
【答案提交】 11027421
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
int main(){
//设 有 x 个 ‘0’ 和 y 个 ‘1’ ;则有x+y= 23333333,即 y=23333333-x ,
// 因为题目告诉了 0 出现次数比 1 少,也即是 x<=23333333/2 ,
// ‘0’占比 x/(x+y)
// ‘1’占比 y/(x+y)
//计算机最不怕的就是麻烦,开找
double Hs=11625907.5798;
for(double x=23333333/2; x>=1; x-- ){ //刷题经验给我的感觉就是要求的 x 一定很大,所以我选择反过来循环
double y=23333333-x;
double p0=x/(x+y);
double p1=y/(x+y); // p1=1.0-p0;
double result = x * ( - p0 * ( log(p0)/log(2) ) ) + y * ( - p1 * ( log(p1)/log(2) ) );
if(11625907.5797<result && result<11625907.5799) //精度问题,没办法用等于
printf("x=%.0f result=%f\n",x,result);
}
return 0;
}
试题 C: 冶炼金属
时间限制: 1.0s 内存限制: 256.0MB 本题总分:10 分
【问题描述】
小蓝有一个神奇的炉子用于将普通金属 O 冶炼成为一种特殊金属 X。这个 炉子有一个称作转换率的属性 V,V 是一个正整数,这意味着消耗 V 个普通金 属 O 恰好可以冶炼出一个特殊金属 X,当普通金属 O 的数目不足 V 时,无法 继续冶炼。 现在给出了 N 条冶炼记录,每条记录中包含两个整数 A 和 B,这表示本次 投入了 A 个普通金属 O,最终冶炼出了 B 个特殊金属 X。每条记录都是独立 的,这意味着上一次没消耗完的普通金属 O 不会累加到下一次的冶炼当中。 根据这 N 条冶炼记录,请你推测出转换率 V 的最小值和最大值分别可能是 多少,题目保证评测数据不存在无解的情况。
【输入格式】
第一行一个整数 N,表示冶炼记录的数目。 接下来输入 N 行,每行两个整数 A、B,含义如题目所述。
【输出格式】
输出两个整数,分别表示 V 可能的最小值和最大值,中间用空格分开。
【样例输入】
3
75 3
53 2
59 2
【样例输出】
20 25
【样例说明】
当 V = 20 时,有:⌊ 75/ 20 ⌋ = 3,⌊ 53/ 20 ⌋ = 2,⌊ 59/ 20 ⌋ = 2,可以看到符合所有冶炼 记录。
当 V = 25 时,有:⌊ 75 /25 ⌋ = 3,⌊ 53/ 25 ⌋ = 2,⌊ 59/ 25 ⌋ = 2,可以看到符合所有冶炼记录。
且再也找不到比 20 更小或者比 25 更大的符合条件的 V 值了。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ N ≤ 10^2。
对于 60% 的评测用例,1 ≤ N ≤ 10^3。
对于 100% 的评测用例,1 ≤ N ≤ 10^4,1 ≤ B ≤ A ≤ 10^9。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
int main(){ //10分题,想啥呢,没那么负责,很简单的,每次都判断可去范围就好了
int V_max=0x3f3f3f3f ,V_min=0;
int N;
cin>>N;
while(N--){
int A,B;
cin>>A>>B;
//本次中,冶炼一个特殊金属至少消耗 Vmin 才能满足本次冶炼 B 个的条件
int Vmin=A/(B+1)+1;
//本次中,冶炼一个特殊金属最多消耗 Vmax 才能满足本次冶炼 B 个的条件
int Vmax=A/B;
V_min=max(V_min, Vmin); //所有最小消耗中取最大值才能都满足
V_max=min(V_max, Vmax); //所有最大消耗中取最小值才能都满足
}
cout<<V_min<<" "<<V_max<<endl;
return 0;
}
试题 D: 飞机降落
时间限制: 2.0s 内存限制: 256.0MB 本题总分:10 分
【问题描述】
N 架飞机准备降落到某个只有一条跑道的机场。其中第 i 架飞机在 Ti 时刻 到达机场上空,到达时它的剩余油料还可以继续盘旋 Di 个单位时间,即它最早 可以于 Ti 时刻开始降落,最晚可以于 Ti + Di 时刻开始降落。降落过程需要 Li 个单位时间。 一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落,但是不 能在前一架飞机完成降落前开始降落。 请你判断 N 架飞机是否可以全部安全降落。
【输入格式】
输入包含多组数据。 第一行包含一个整数 T,代表测试数据的组数。 对于每组数据,第一行包含一个整数 N。 以下 N 行,每行包含三个整数:Ti,Di 和 Li。
【输出格式】
对于每组数据,输出 YES 或者 NO,代表是否可以全部安全降落。
【样例输入】
2
3
0 100 10
10 10 10
0 2 20
3
0 10 20
10 10 20
20 10 20
【样例输出】
YES
NO
【样例说明】
对于第一组数据,可以安排第 3 架飞机于 0 时刻开始降落,20 时刻完成降 落。安排第 2 架飞机于 20 时刻开始降落,30 时刻完成降落。安排第 1 架飞机 于 30 时刻开始降落,40 时刻完成降落。
对于第二组数据,无论如何安排,都会有飞机不能及时降落。
【评测用例规模与约定】
对于 30% 的数据,N ≤ 2。
对于 100% 的数据,1 ≤ T ≤ 10,1 ≤ N ≤ 10,0 ≤ Ti , Di , Li ≤ 10^5。
不出意外的话,我估计此题解法仅对50%的测评有效
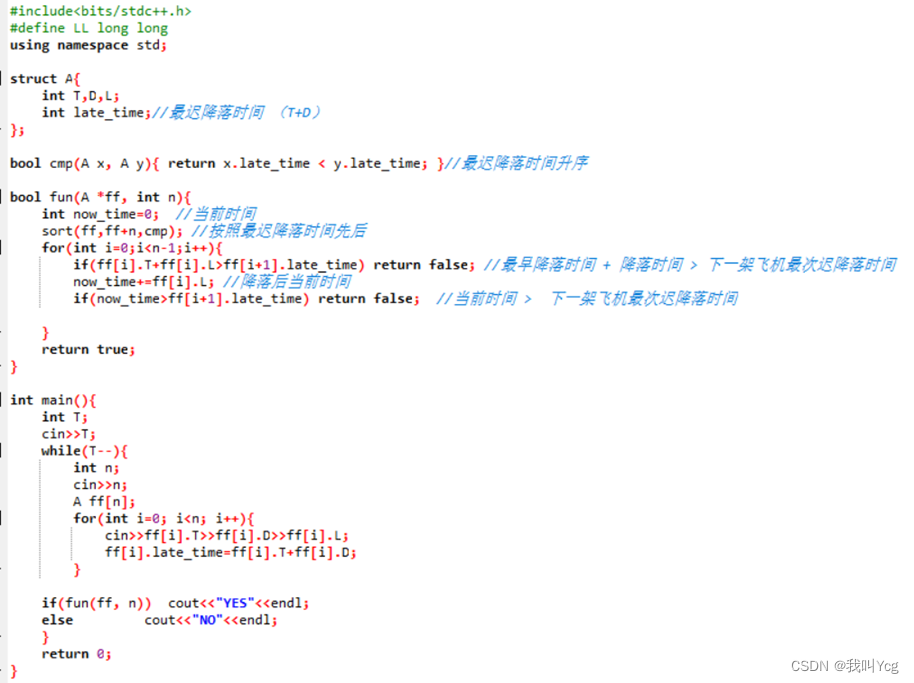
#include<bits/stdc++.h>
#define LL long long
using namespace std;
struct A{
int T,D,L;
int late_time;//最迟降落时间 (T+D)
};
bool cmp(A x, A y){ return x.late_time < y.late_time; }//最迟降落时间升序
bool fun(A *ff, int n){
int now_time=0; //当前时间
sort(ff,ff+n,cmp); //按照最迟降落时间先后
for(int i=0;i<n-1;i++){
if(ff[i].T+ff[i].L>ff[i+1].late_time) return false; //最早降落时间 + 降落时间 > 下一架飞机最次迟降落时间
now_time+=ff[i].L; //降落后当前时间
if(now_time>ff[i+1].late_time) return false; //当前时间 > 下一架飞机最次迟降落时间
}
return true;
}
int main(){
int T;
cin>>T;
while(T--){
int n;
cin>>n;
A ff[n];
for(int i=0; i<n; i++){
cin>>ff[i].T>>ff[i].D>>ff[i].L;
ff[i].late_time=ff[i].T+ff[i].D;
}
if(fun(ff, n)) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
return 0;
}
试题 E: 接龙数列
时间限制: 1.0s 内存限制: 256.0MB 本题总分:15 分
【问题描述】
对于一个长度为 K 的整数数列:A1, A2, . . . , AK,我们称之为接龙数列当且 仅当 Ai 的首位数字恰好等于 Ai−1 的末位数字 (2 ≤ i ≤ K)。 例如 12, 23, 35, 56, 61, 11 是接龙数列;12, 23, 34, 56 不是接龙数列,因为 56 的首位数字不等于 34 的末位数字。所有长度为 1 的整数数列都是接龙数列。 现在给定一个长度为 N 的数列 A1, A2, . . . , AN,请你计算最少从中删除多少 个数,可以使剩下的序列是接龙序列?
【输入格式】
第一行包含一个整数 N。 第二行包含 N 个整数 A1, A2, . . . , AN。
【输出格式】
一个整数代表答案。
【样例输入】
5
11 121 22 12 2023
【样例输出】
1
【样例说明】
删除 22,剩余 11, 121, 12, 2023 是接龙数列。
【评测用例规模与约定】
对于 20% 的数据,1 ≤ N ≤ 20。
对于 50% 的数据,1 ≤ N ≤ 10000。
对于 100% 的数据,1 ≤ N ≤ 10^5,1 ≤ Ai ≤ 10^9。所有 Ai 保证不包含前导 0。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
//(我下意识想到了第一题)题目要求的是 最少 从中删除多少个数,
// 也就是求最长的接龙子序列嘛
// 动态规划典型例题之一:求最长子序列
// 虽然才到第5题,但是今年蓝桥杯明显想搞事情,动态规划就动态规划嘛,搞这么隐秘干嘛。
int tou[100005],wei[100005];//第 i 个数的头、第 i 个数的尾
int dp[100005];// dp[i]:表示前 i 个数中,以第 i 个数作为子序列结尾的最长的接龙子序列长度
// 注意:不以 i 结尾的接龙子序列也可能会更长
int main(){
int n;
cin>>n;
for(int i=0; i<n; i++){
string s;
cin>>s;
tou[i]=s[0]-'0'; //头
wei[i]=s[s.size()-1]-'0'; //尾
}
int max_size=0; //记录过程中最长接龙子序列
for(int i=0; i<n; i++){
dp[i]=1;
for(int j=0; j<i; j++){
if(wei[j]==tou[i]) //第 j (j<i)个数的尾b[j]等于第 i 个数的头a[i]时
dp[i]=max(dp[i],dp[j]+1); //拼接成功,长度 + 1
}
max_size=max(max_size,dp[i]);
}
cout<<n-max_size;
return 0;
}
试题 F: 岛屿个数
时间限制: 2.0s 内存限制: 256.0MB 本题总分:15 分
【问题描述】
小蓝得到了一副大小为 M × N 的格子地图,可以将其视作一个只包含字符 ‘0’(代表海水)和 ‘1’(代表陆地)的二维数组,地图之外可以视作全部是海水, 每个岛屿由在上/下/左/右四个方向上相邻的 ‘1’ 相连接而形成。 在岛屿 A 所占据的格子中,如果可以从中选出 k 个不同的格子,使得 他们的坐标能够组成一个这样的排列:(x0, y0),(x1, y1), . . . ,(xk−1, yk−1),其中 (x(i+1)%k , y(i+1)%k) 是由 (xi , yi) 通过上/下/左/右移动一次得来的 (0 ≤ i ≤ k − 1), 此时这 k 个格子就构成了一个 “环”。如果另一个岛屿 B 所占据的格子全部位于 这个 “环” 内部,此时我们将岛屿 B 视作是岛屿 A 的子岛屿。若 B 是 A 的子 岛屿,C 又是 B 的子岛屿,那 C 也是 A 的子岛屿。 请问这个地图上共有多少个岛屿?在进行统计时不需要统计子岛屿的数目。
【输入格式】
第一行一个整数 T,表示有 T 组测试数据。 接下来输入 T 组数据。对于每组数据,第一行包含两个用空格分隔的整数 M、N 表示地图大小;接下来输入 M 行,每行包含 N 个字符,字符只可能是 ‘0’ 或 ‘1’。
【输出格式】
对于每组数据,输出一行,包含一个整数表示答案。
【样例输入】
2
5 5
01111
11001
10101
10001
11111
5 6
111111
100001
010101
100001
111111
【样例输出】
1
3
【样例说明】
对于第一组数据,包含两个岛屿,下面用不同的数字进行了区分: 01111 11001 10201 10001 11111 岛屿 2 在岛屿 1 的 “环” 内部,所以岛屿 2 是岛屿 1 的子岛屿,答案为 1。 对于第二组数据,包含三个岛屿,下面用不同的数字进行了区分: 111111 100001 020301 100001 111111
注意岛屿 3 并不是岛屿 1 或者岛屿 2 的子岛屿,因为岛屿 1 和岛屿 2 中均没有 “环”。
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ M, N ≤ 10。
对于 100% 的评测用例,1 ≤ T ≤ 10,1 ≤ M, N ≤ 50。
个人而言,这题对我最难,也是代码写的最长的
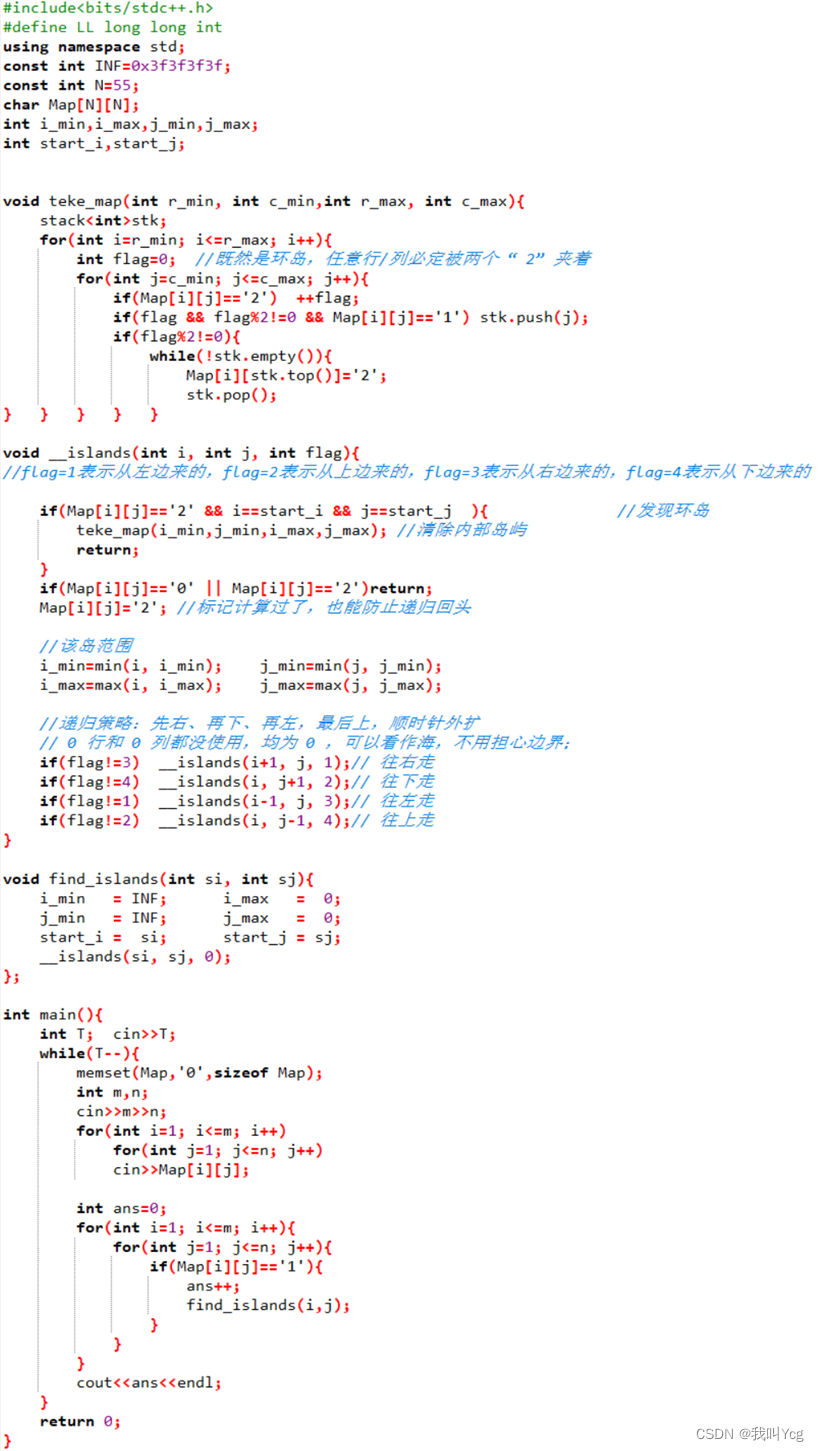
#include<bits/stdc++.h>
#define LL long long int
using namespace std;
const int INF=0x3f3f3f3f;
const int N=55;
char Map[N][N];
int i_min,i_max,j_min,j_max;
int start_i,start_j;
void teke_map(int r_min, int c_min,int r_max, int c_max){
stack<int>stk;
for(int i=r_min; i<=r_max; i++){
int flag=0; //既然是环岛,任意行/列必定被两个 “2”夹着
for(int j=c_min; j<=c_max; j++){
if(Map[i][j]=='2') ++flag;
if(flag && flag%2!=0 && Map[i][j]=='1') stk.push(j);
if(flag%2!=0){
while(!stk.empty()){
Map[i][stk.top()]='2';
stk.pop();
} } } } }
void __islands(int i, int j, int flag){
//flag=1表示从左边来的,flag=2表示从上边来的,flag=3表示从右边来的,flag=4表示从下边来的
if(Map[i][j]=='2' && i==start_i && j==start_j ){ //发现环岛
teke_map(i_min,j_min,i_max,j_max); //清除内部岛屿
return;
}
if(Map[i][j]=='0' || Map[i][j]=='2')return;
Map[i][j]='2'; //标记计算过了,也能防止递归回头
//该岛范围
i_min=min(i, i_min); j_min=min(j, j_min);
i_max=max(i, i_max); j_max=max(j, j_max);
//递归策略:先右、再下、再左,最后上,顺时针外扩
// 0 行和 0 列都没使用,均为 0 ,可以看作海,不用担心边界;
if(flag!=3) __islands(i+1, j, 1);// 往右走
if(flag!=4) __islands(i, j+1, 2);// 往下走
if(flag!=1) __islands(i-1, j, 3);// 往左走
if(flag!=2) __islands(i, j-1, 4);// 往上走
}
void find_islands(int si, int sj){
i_min = INF; i_max = 0;
j_min = INF; j_max = 0;
start_i = si; start_j = sj;
__islands(si, sj, 0);
};
int main(){
int T; cin>>T;
while(T--){
memset(Map,'0',sizeof Map);
int m,n;
cin>>m>>n;
for(int i=1; i<=m; i++)
for(int j=1; j<=n; j++)
cin>>Map[i][j];
int ans=0;
for(int i=1; i<=m; i++){
for(int j=1; j<=n; j++){
if(Map[i][j]=='1'){
ans++;
find_islands(i,j);
}
}
}
cout<<ans<<endl;
}
return 0;
}
试题 G: 子串简写
时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
【问题描述】
程序猿圈子里正在流行一种很新的简写方法:对于一个字符串,只保留首 尾字符,将首尾字符之间的所有字符用这部分的长度代替。例如 internationalization 简写成 i18n,Kubernetes (注意连字符不是字符串的一部分)简 写成 K8s, Lanqiao 简写成 L5o 等。 在本题中,我们规定长度大于等于 K 的字符串都可以采用这种简写方法 (长度小于 K 的字符串不配使用这种简写)。 给定一个字符串 S 和两个字符 c1 和 c2,请你计算 S 有多少个以 c1 开头 c2 结尾的子串可以采用这种简写?
【输入格式】
第一行包含一个整数 K。
第二行包含一个字符串 S 和两个字符 c1 和 c2。
【输出格式】
一个整数代表答案。
【样例输入】
4
abababdb a b
【样例输出】
6
【样例说明】
符合条件的子串如下所示,中括号内是该子串:
[abab]abdb
[ababab]db
[abababdb]
ab[abab]db
ab[ababdb]
abab[abdb]
【评测用例规模与约定】
对于 20% 的数据,2 ≤ K ≤ |S | ≤ 10000。
对于 100% 的数据,2 ≤ K ≤ |S | ≤ 5 × 105。S 只包含小写字母。c1 和 c2 都是小写字母。 |S | 代表字符串 S 的长度。
20分呀,简单得有点过分了,不太相信,估计是有什么坑,比如超时。
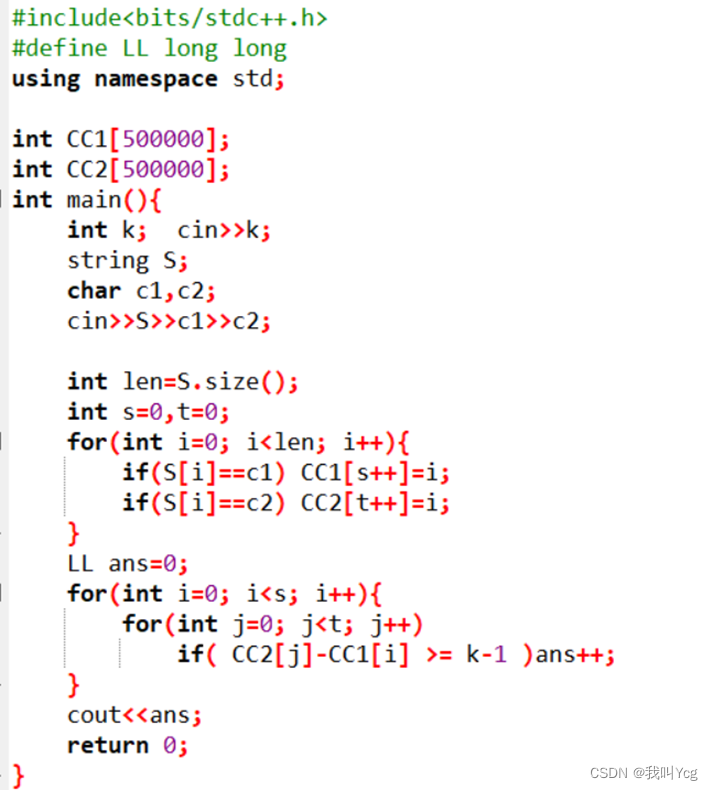
#include<bits/stdc++.h>
#define LL long long
using namespace std;
int CC1[500000];
int CC2[500000];
int main(){
int k; cin>>k;
string S;
char c1,c2;
cin>>S>>c1>>c2;
int len=S.size();
int s=0,t=0;
for(int i=0; i<len; i++){
if(S[i]==c1) CC1[s++]=i;
if(S[i]==c2) CC2[t++]=i;
}
LL ans=0;
for(int i=0; i<s; i++){
for(int j=0; j<t; j++)
if( CC2[j]-CC1[i] >= k-1 )ans++;
}
cout<<ans;
return 0;
}
试题 H: 整数删除
时间限制: 1.0s 内存限制: 256.0MB 本题总分:20 分
【问题描述】
给定一个长度为 N 的整数数列:A1, A2, . . . , AN。你要重复以下操作 K 次:
每次选择数列中最小的整数(如果最小值不止一个,选择最靠前的),将其删除。并把与它相邻的整数加上被删除的数值。 输出 K 次操作后的序列。
【输入格式】
第一行包含两个整数 N 和 K。 第二行包含 N 个整数,A1, A2, A3, . . . , AN。
【输出格式】
输出 N − K 个整数,中间用一个空格隔开,代表 K 次操作后的序列。
【样例输入】
5 3
1 4 2 8 7
【样例输出】
17 7
【样例说明】
数列变化如下,中括号里的数是当次操作中被选择的数:
[1] 4 2 8 7
5 [2] 8 7
[7] 10 7
17 7
【评测用例规模与约定】
对于 20% 的数据,1 ≤ K < N ≤ 10000。
对于 100% 的数据,1 ≤ K < N ≤ 5 × 10^5,0 ≤ Ai ≤ 10^8。

#include<bits/stdc++.h>
#define LL long long
using namespace std;
map<int, int >k_v_map;
bool cmp(const pair<int, int> left,const pair<int,int> right){
return left.second < right.second;
}
int main(){
int N,K;
cin>>N>>K;
for(int i=0; i<N; i++){
cin>>k_v_map[i];
}
map<int, int>::iterator it; //迭代指针
while(K--){
it = min_element(k_v_map.begin(),k_v_map.end(),cmp);//获取最小值键值对的迭代指针
int Ai=it->second; //最小值
if(it!=k_v_map.begin()){//不是第一个时
it--;
it->second+=Ai; //前一个元素加上 Ai
it++;
}
if(it!=k_v_map.end()){//不是第一个时
it++;
it->second+=Ai; //后一个元素加上 Ai
it--;
}
k_v_map.erase(it); //删除最小值键值对
}
for(it = k_v_map.begin(); it != k_v_map.end(); it++)
cout<<it->second<<" ";//输出value值
return 0;
}
试题 I: 景区导游
时间限制: 5.0s 内存限制: 256.0MB 本题总分:25 分
【问题描述】
某景区一共有 N 个景点,编号 1 到 N。景点之间共有 N − 1 条双向的摆渡车线路相连,形成一棵树状结构。在景点之间往返只能通过这些摆渡车进行, 需要花费一定的时间。 小明是这个景区的资深导游,他每天都要按固定顺序带客人游览其中 K 个 景点:A1, A2, . . . , AK。今天由于时间原因,小明决定跳过其中一个景点,只带游客按顺序游览其中 K − 1 个景点。具体来说,如果小明选择跳过 Ai,那么他会 按顺序带游客游览 A1, A2, . . . , Ai−1, Ai+1, . . . , AK, (1 ≤ i ≤ K)。 请你对任意一个 Ai,计算如果跳过这个景点,小明需要花费多少时间在景 点之间的摆渡车上?
【输入格式】
第一行包含 2 个整数 N 和 K。 以下 N − 1 行,每行包含 3 个整数 u, v 和 t,代表景点 u 和 v 之间有摆渡车线路,花费 t 个单位时间。 最后一行包含 K 个整数 A1, A2, . . . , AK 代表原定游览线路。
【输出格式】
输出 K 个整数,其中第 i 个代表跳过 Ai 之后,花费在摆渡车上的时间。
【样例输入】
6 4
1 2 1
1 3 1
3 4 2
3 5 2
4 6 3
2 6 5 1
【样例输出】
10 7 13 14
【样例说明】
原路线是 2 → 6 → 5 → 1。
当跳过 2 时,路线是 6 → 5 → 1,其中 6 → 5 花费时间 3 + 2 + 2 = 7, 5 → 1 花费时间 2 + 1 = 3,总时间花费 10。
当跳过 6 时,路线是 2 → 5 → 1,其中 2 → 5 花费时间 1 + 1 + 2 = 4, 5 → 1 花费时间 2 + 1 = 3,总时间花费 7。
当跳过 5 时,路线是 2 → 6 → 1,其中 2 → 6 花费时间 1 + 1 + 2 + 3 = 7, 6 → 1 花费时间 3 + 2 + 1 = 6,总时间花费 13。
当跳过 1 时,路线时 2 → 6 → 5,其中 2 → 6 花费时间 1 + 1 + 2 + 3 = 7, 6 → 5 花费时间 3 + 2 + 2 = 7,总时间花费 14。
【评测用例规模与约定】
对于 20% 的数据,2 ≤ K ≤ N ≤ 10^2。
对于 40% 的数据,2 ≤ K ≤ N ≤ 10^4。
对于 100% 的数据,2 ≤ K ≤ N ≤ 10^5,1 ≤ u, v, Ai ≤ N,1 ≤ t ≤ 10^5。保证 Ai 两两不同。
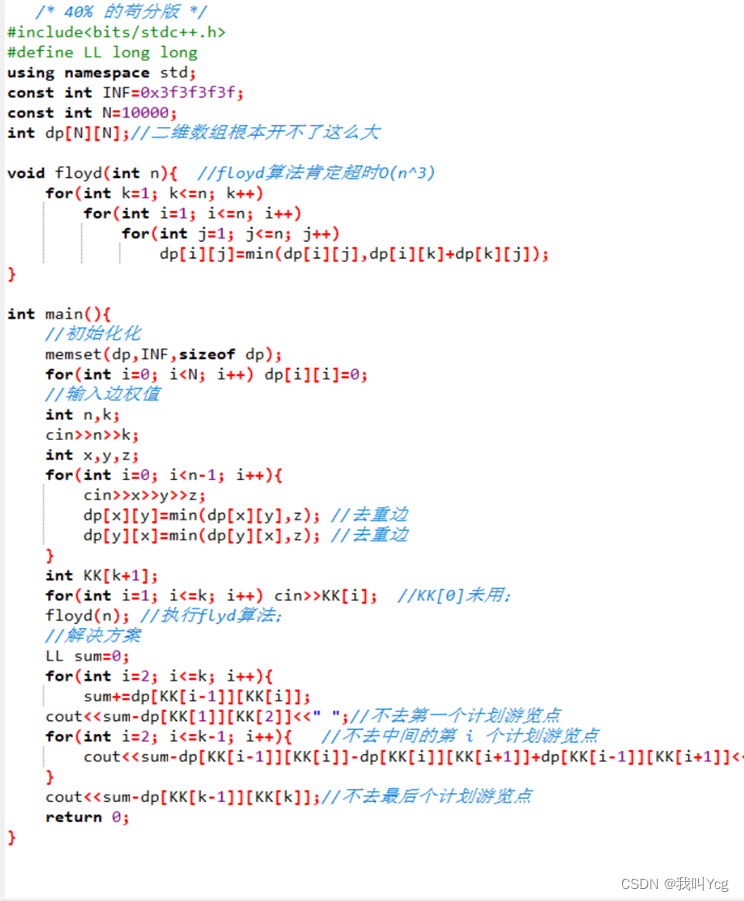
/* 40% 的苟分版 */
#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int INF=0x3f3f3f3f;
const int N=10000;
int dp[N][N];//二维数组根本开不了这么大
void floyd(int n){ //floyd算法肯定超时O(n^3)
for(int k=1; k<=n; k++)
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);
}
int main(){
//初始化化
memset(dp,INF,sizeof dp);
for(int i=0; i<N; i++) dp[i][i]=0;
//输入边权值
int n,k;
cin>>n>>k;
int x,y,z;
for(int i=0; i<n-1; i++){
cin>>x>>y>>z;
dp[x][y]=min(dp[x][y],z); //去重边
dp[y][x]=min(dp[y][x],z); //去重边
}
int KK[k+1];
for(int i=1; i<=k; i++) cin>>KK[i]; //KK[0]未用;
floyd(n); //执行flyd算法;
//解决方案
LL sum=0;
for(int i=2; i<=k; i++){
sum+=dp[KK[i-1]][KK[i]];
cout<<sum-dp[KK[1]][KK[2]]<<" ";//不去第一个计划游览点
for(int i=2; i<=k-1; i++){ //不去中间的第 i 个计划游览点
cout<<sum-dp[KK[i-1]][KK[i]]-dp[KK[i]][KK[i+1]]+dp[KK[i-1]][KK[i+1]]<<" ";
}
cout<<sum-dp[KK[k-1]][KK[k]];//不去最后个计划游览点
return 0;
}
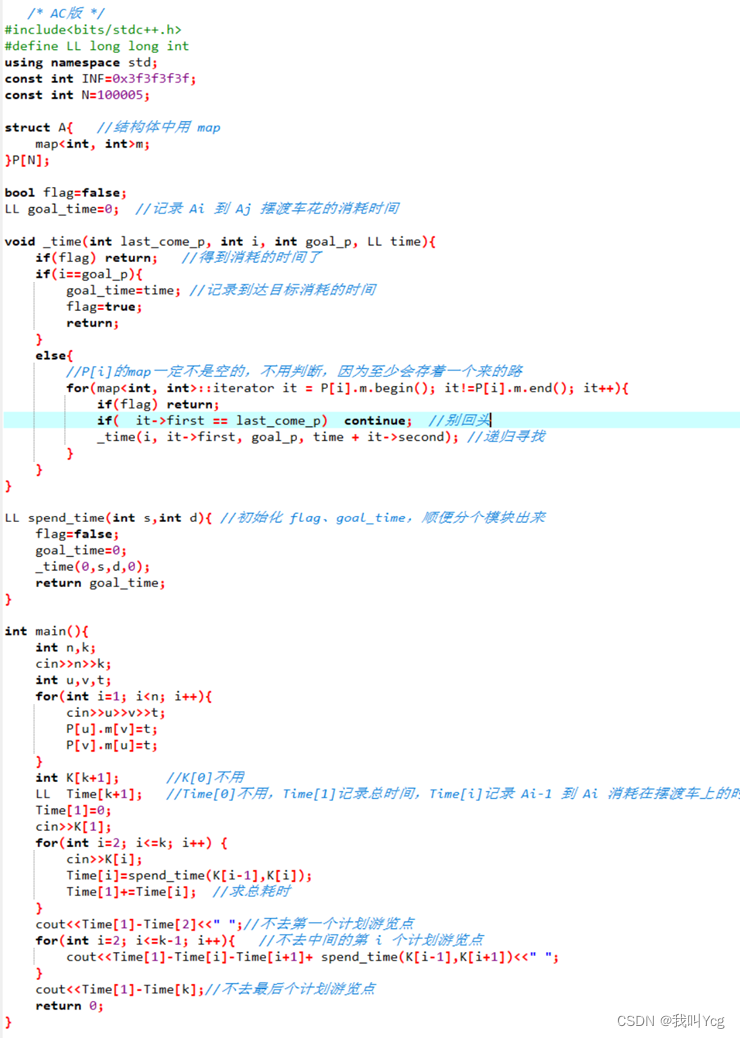
/* AC版 */
#include<bits/stdc++.h>
#define LL long long int
using namespace std;
const int INF=0x3f3f3f3f;
const int N=100005;
struct A{ //结构体中用 map
map<int, int>m;
}P[N];
bool flag=false;
LL goal_time=0; //记录 Ai 到 Aj 摆渡车花的消耗时间
void _time(int last_come_p, int i, int goal_p, LL time){
if(flag) return; //得到消耗的时间了
if(i==goal_p){
goal_time=time; //记录到达目标消耗的时间
flag=true;
return;
}
else{
//P[i]的map一定不是空的,不用判断,因为至少会存着一个来的路
for(map<int, int>::iterator it = P[i].m.begin(); it!=P[i].m.end(); it++){
if(flag) return;
if( it->first == last_come_p) continue; //别回头
_time(i, it->first, goal_p, time + it->second); //递归寻找
}
}
}
LL spend_time(int s,int d){ //初始化 flag、goal_time,顺便分个模块出来
flag=false;
goal_time=0;
_time(0,s,d,0);
return goal_time;
}
int main(){
int n,k;
cin>>n>>k;
int u,v,t;
for(int i=1; i<n; i++){
cin>>u>>v>>t;
P[u].m[v]=t;
P[v].m[u]=t;
}
int K[k+1]; //K[0]不用
LL Time[k+1]; //Time[0]不用,Time[1]记录总时间,Time[i]记录 Ai-1 到 Ai 消耗在摆渡车上的时间
Time[1]=0;
cin>>K[1];
for(int i=2; i<=k; i++) {
cin>>K[i];
Time[i]=spend_time(K[i-1],K[i]);
Time[1]+=Time[i]; //求总耗时
}
cout<<Time[1]-Time[2]<<" ";//不去第一个计划游览点
for(int i=2; i<=k-1; i++){ //不去中间的第 i 个计划游览点
cout<<Time[1]-Time[i]-Time[i+1]+ spend_time(K[i-1],K[i+1])<<" ";
}
cout<<Time[1]-Time[k];//不去最后个计划游览点
return 0;
}
试题 J: 砍树
时间限制: 1.0s 内存限制: 256.0MB 本题总分:25 分
【问题描述】
给定一棵由 n 个结点组成的树以及 m 个不重复的无序数对 (a1, b1), (a2, b2), . . . , (am, bm),其中 ai 互不相同,bi 互不相同,ai , bj(1 ≤ i, j ≤ m)。 小明想知道是否能够选择一条树上的边砍断,使得对于每个 (ai , bi) 满足 ai 和 bi 不连通,如果可以则输出应该断掉的边的编号(编号按输入顺序从 1 开 始),否则输出 -1。
【输入格式】
输入共 n + m 行,第一行为两个正整数 n,m。 后面 n − 1 行,每行两个正整数 xi,yi 表示第 i 条边的两个端点。 后面 m 行,每行两个正整数 ai,bi。
【输出格式】
一行一个整数,表示答案,如有多个答案,输出编号最大的一个。
【样例输入】
6 2
1 2
2 3
4 3
2 5
6 5
3 6
4 5
【样例输出】
4
【样例说明】
断开第 2 条边后形成两个连通块:{3, 4},{1, 2, 5, 6},满足 3 和 6 不连通,4 和 5 不连通。 断开第 4 条边后形成两个连通块:{1, 2, 3, 4},{5, 6},同样满足 3 和 6 不连 通,4 和 5 不连通。 4 编号更大,因此答案为 4。
【评测用例规模与约定】
对于 30% 的数据,保证 1 < n ≤ 1000。
对于 100% 的数据,保证 1 < n ≤ 10^5,1 ≤ m ≤ n/2。
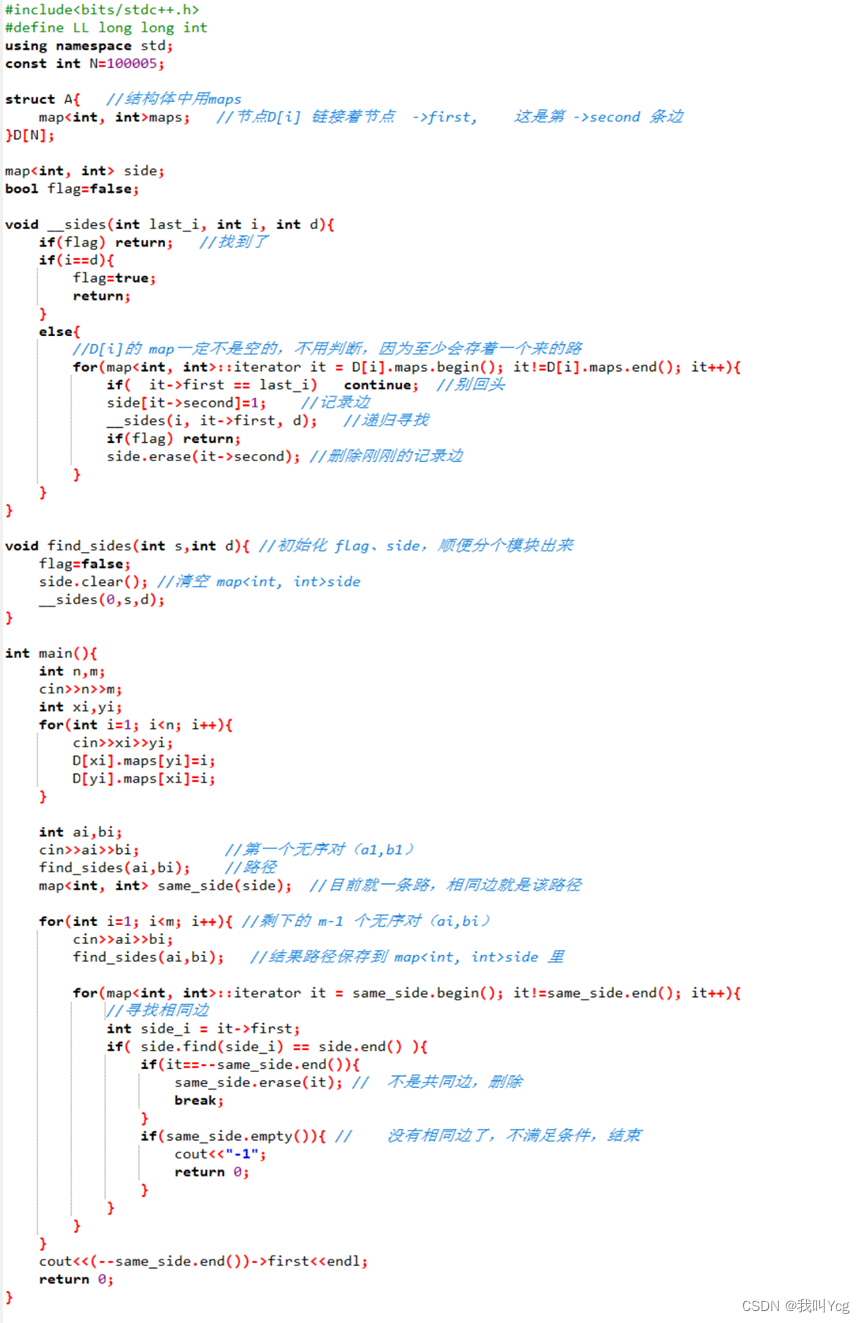
#include<bits/stdc++.h>
#define LL long long int
using namespace std;
const int N=100005;
struct A{ //结构体中用maps
map<int, int>maps; //节点D[i] 链接着节点 ->first, 这是第 ->second 条边
}D[N];
map<int, int> side;
bool flag=false;
void __sides(int last_i, int i, int d){
if(flag) return; //找到了
if(i==d){
flag=true;
return;
}
else{
//D[i]的 map一定不是空的,不用判断,因为至少会存着一个来的路
for(map<int, int>::iterator it = D[i].maps.begin(); it!=D[i].maps.end(); it++){
if( it->first == last_i) continue; //别回头
side[it->second]=1; //记录边
__sides(i, it->first, d); //递归寻找
if(flag) return;
side.erase(it->second); //删除刚刚的记录边
}
}
}
void find_sides(int s,int d){ //初始化 flag、side,顺便分个模块出来
flag=false;
side.clear(); //清空 map<int, int>side
__sides(0,s,d);
}
int main(){
int n,m;
cin>>n>>m;
int xi,yi;
for(int i=1; i<n; i++){
cin>>xi>>yi;
D[xi].maps[yi]=i;
D[yi].maps[xi]=i;
}
int ai,bi;
cin>>ai>>bi; //第一个无序对(a1,b1)
find_sides(ai,bi); //路径
map<int, int> same_side(side); //目前就一条路,相同边就是该路径
for(int i=1; i<m; i++){ //剩下的 m-1 个无序对(ai,bi)
cin>>ai>>bi;
find_sides(ai,bi); //结果路径保存到 map<int, int>side 里
for(map<int, int>::iterator it = same_side.begin(); it!=same_side.end(); it++){
//寻找相同边
int side_i = it->first;
if( side.find(side_i) == side.end() ){
if(it==--same_side.end()){
same_side.erase(it); // 不是共同边,删除
break;
}
if(same_side.empty()){ // 没有相同边了,不满足条件,结束
cout<<"-1";
return 0;
}
}
}
}
cout<<(--same_side.end())->first<<endl;
return 0;
}
