图嵌入 Node2Vec
文章目录
- 图嵌入之 Node2Vec
- 1 两个概念
- 2 两种节点采样方法
- 3 Node2Vec 中的二阶 Random Walk
- 3.1 Random Walks 的定义
- 3.2 搜索偏置 α \alpha α
- 4 二阶 Random Walk 的优势
- 5 算法步骤
图嵌入之 Node2Vec
论文地址 https://arxiv.org/pdf/1607.00653.pdf
对 Random Walk 中随机地选择游走序列进行了改进,别的地方与 Deep Walk 大致相同
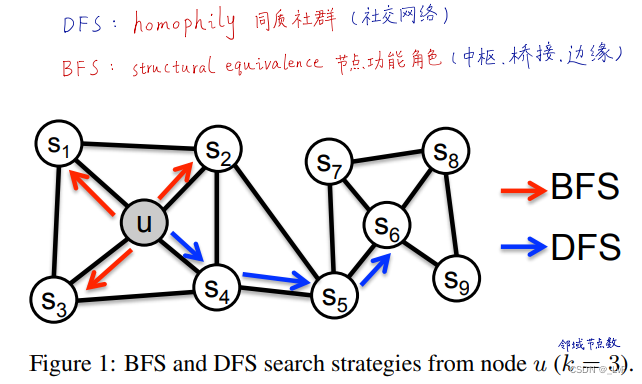
1 两个概念
-
homophily:同质性,越是相邻的节点同质的趋势更大
-
structural equivalence:结构相似性,如 Figure 1 中 u 节点和 S 6 S_6 S6 节点在结构上很相似
2 两种节点采样方法
-
广度优先采样BFS:采样的节点序列更能挖掘结构相似性(微观)
-
深度优先采样DFS:采样的节点序列更能挖掘同质性(宏观)
3 Node2Vec 中的二阶 Random Walk
3.1 Random Walks 的定义
设 c i c_i ci 表示随机游走中的第 i 个节点, c i c_i ci 的选择遵循如下分布:
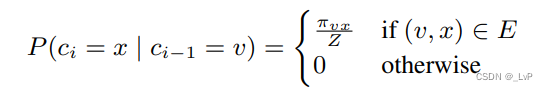
π v x \pi_{vx} πvx 表示节点 v v v 和 x x x 之间未归一化的过渡概率, Z Z Z 是进行归一化的常数
即从当前节点 v 到下一个节点 x 的条件概率等于 π v x Z \frac{\pi_{vx}}{Z} Zπvx, π v x \pi_{vx} πvx 怎么算往下看
3.2 搜索偏置 α \alpha α
定义两个参数 p p p 和 q q q (超参数)来引导随机序列的选择,
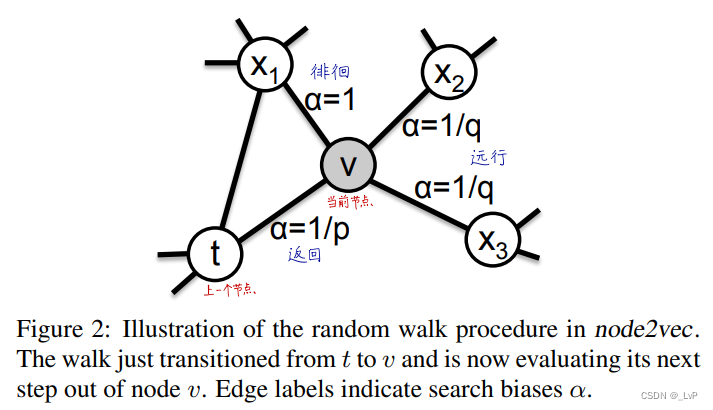
返回参数 p p p(Return parameter):控制从一个节点回退一步的似然,在 Figure 2中,设 t 为走过的上一个节点,v 为当前节点,用 α = 1 / p \alpha=1/p α=1/p 表示从 v 到 t 的权重
区分似然(likelihood)与 概率(probability)
- 对于联合概率函数 P ( y i ^ ∣ x i , θ ) P(\hat{y_i}|x_i,θ) P(yi^∣xi,θ) 而言。
- 概率探究的是自变量与因变量之间的关系,即 θ \theta θ 已知,在不同的特征向量 x i x_i xi 下,得到 y i ^ \hat{y_i} yi^ 的可能性。
- 似然探究的是参数向量与因变量之间的关系,即 x i x_i xi 已知,在不同的参数向量 θ \theta θ 下,得到 y i ^ \hat{y_i} yi^ 的可能性。
进出参数 q q q(In-out parameter):若 q > 1 q > 1 q>1,随机游走算法会偏向于选择,当前节点局部范围(local view)内的节点,类似 BFS ;若 q < 1 q < 1 q<1,随机游走算法倾向于选择更深一步(further away)的节点,类似 DFS
基于边的权重来对下一个节点进行采样,定义边的权重 π v x = α p q ( t , x ) ∗ w v x \pi_{vx} = \alpha_{pq}(t,x)*w_{vx} πvx=αpq(t,x)∗wvx,当前节点到下一个节点的转移概率由 α \alpha α 进行加权,其中 α \alpha α 定义为:
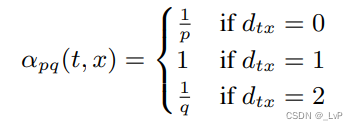
d t x d_{tx} dtx 表示节点 t 到节点 x 的最短路径长度
4 二阶 Random Walk 的优势
快!


5 算法步骤

