当前位置：首页 > article >正文

Adam优化器算法详解及代码实现

article 2025/1/14 18:15:58

文章目录

学习率调整与梯度估计修正
- RMSprop 算法
- 动量法
Adam

学习率调整与梯度估计修正

在介绍Adam算法之前，先谈谈Adam中两个关键的算法：学习率调整（RMSprop 算法）与梯度估计修正。

RMSprop 算法

学习率是神经网络优化时的重要超参数。在标准的梯度下降法中，每个参数在每次迭代时都使用相同的学习率，但是学习率如果过大就不会收敛，如果过小则收敛速度太慢。

RMSprop 算法是 Geoff Hinton 提出的一种自适应学习率的方法【RMSprop】，可以在有些情况下避免 AdaGrad 算法中学习率不断单调下降以至于过早衰减的缺点。

RMSprop 算法首先计算每次迭代梯度 𝒈𝑡 平方的指数衰减移动平均𝐺𝑡 :
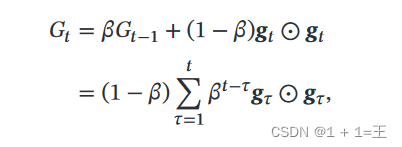
在这里插入图片描述

其中，β为自定义衰减率（例如0.9）。

然后，根据指数衰减移动平均𝐺𝑡 计算参数更新差值Δ𝜃𝑡 ：
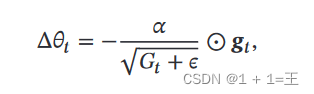
在这里插入图片描述
其中， 𝛼 是初始的学习率，𝜖 是为了保持数值稳定性而设置的非常小的常数。

动量法

在随机（小批量）梯度下降法中，如果每次选取样本数量比较小，损失会呈现振荡的方式下降．也就是说，随机梯度下降方法中每次迭代的梯度估计和整个训练集上的最优梯度并不一致，具有一定的随机性。一种有效地缓解梯度估计随机性的方式是通过使用最近一段时间内的平均梯度来代替当前时刻的随机梯度来作为参数更新的方向，从而提高优化速度。

动量法用之前积累动量来替代真正的梯度，在第 𝑡 次迭代时，计算负梯度的“加权移动平均”作为参数的更新方向：
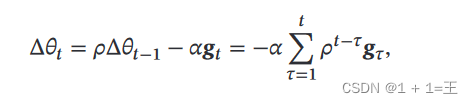
在这里插入图片描述
其中， 𝜌 为动量因子，通常设为 0.9，𝛼 为学习率。

动量法将每个参数的实际更新差值表示为最近一段时间内梯度的加权平均值。在迭代前期，梯度方向都一致，动量法加速参数更新幅度；在迭代后期，剃度方向会不一致，在收敛值附近振荡，动量法会降低参数更新幅度。

类比于物理学，动量法把当前梯度看做当前时刻受理参数的加速度，为了计算当前时刻的速度，应当考虑前一时刻速度和当前加速度共同作用的结果，因此参数的更新直接依赖于前一时刻的更新量和当前时刻的梯度，而不仅仅是当前梯度。另外，𝜌 扮演了阻力的作用。

Adam

Adam是由 OpenAI 的 Diederik Kingma 和多伦多大学的 Jimmy Ba于2015年提出的一种随机优化方法。
在这里插入图片描述

原文链接：ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION：https://arxiv.org/pdf/1412.6980.pdf%5D

Adam算法结合RMSprop 算法和动量法，不但使用动量作为参数更新方向，而且可以自适应调整学习率来改进梯度下降。

计算梯度平方 g𝑡 平方的指数加权平均（RMSprop ）；

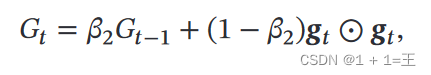
g[:] = beta2 * s + (1 - beta2) * torch.mul(p.grad, p.grad)

计算梯度 g𝑡 的指数加权平均（动量法）；

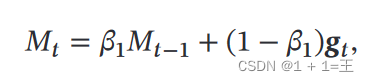
其中， 𝛽1 和 𝛽2 分别为两个移动平均的衰减率，在Adam原文中取值为 𝛽1 = 0.9, 𝛽2 = 0.999。

m[:] = beta1 * v + (1 - beta1) * p.grad

对偏差进行修正

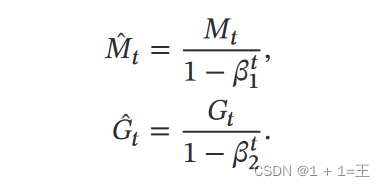
m_bias_corr = m / (1 - beta1 ** hyperparams['t'])
g_bias_corr = g / (1 - beta2 ** hyperparams['t'])

计算参数更新差值

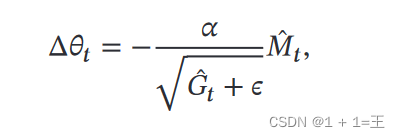
p[:] -= hyperparams['lr'] * m_bias_corr / (torch.sqrt(g_bias_corr) + eps)

在Adam论文原文中，对Adam的算法描述如下：

在这里插入图片描述

下面给出Adam的简单实现：

def adam(params, states, hyperparams):
    beta1, beta2, eps = 0.9, 0.99, 1e-6
    for p, (m, g) in zip(params, states):
        with torch.no_grad():
            m[:] = beta1 * m + (1 - beta1) * p.grad
            g[:] = beta2 * g + (1 - beta2) * torch.mul(p.grad, p.grad)
            m_bias_corr = m / (1 - beta1 ** hyperparams['t'])
            g_bias_corr = g / (1 - beta2 ** hyperparams['t'])
            p[:] -= hyperparams['lr'] * m_bias_corr / (torch.sqrt(g_bias_corr) + eps)
        p.grad.data.zero_()
    hyperparams['t'] += 1