当前位置： 首页 > article >正文

【C语言】迷宫问题

article 2024/11/13 7:55:01

【C语言】迷宫问题

  • 一. 题目描述
  • 二. 思想
    • 2.1 算法---回溯算法
    • 2.2 思路分析+图解
  • 三. 代码实现
    • 3.1 二维数组的实现
    • 3.2 上下左右四个方向的判断
    • 3.4 用栈记录坐标的实现
    • 3.5 完整代码
  • 四. 总结

一. 题目描述

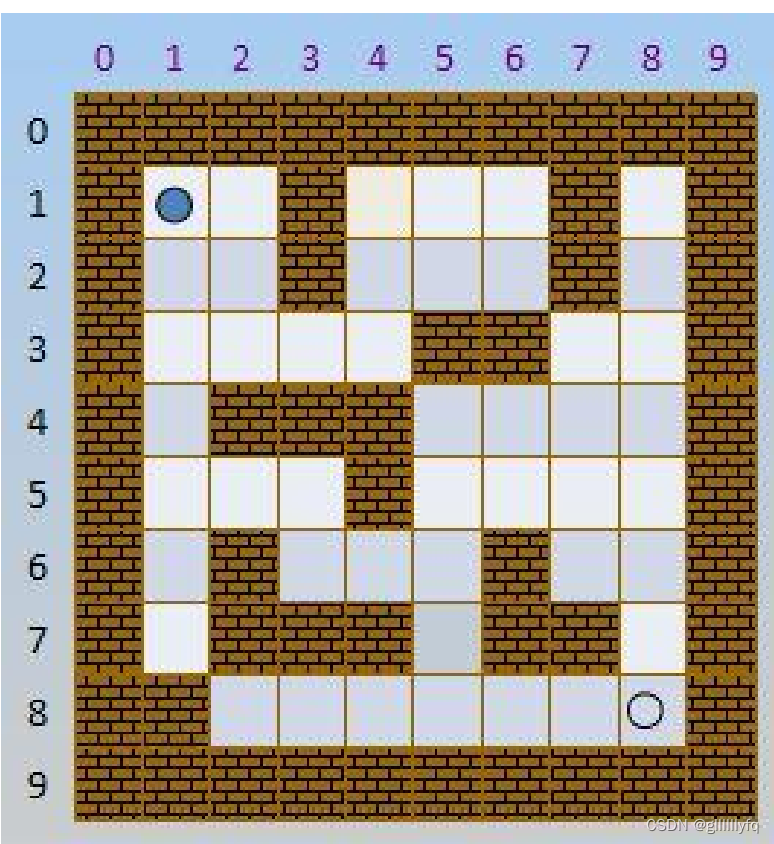
在这里插入图片描述

牛客网链接：https://www.nowcoder.com/questionTerminal/cf24906056f4488c9ddb132f317e03bc

在这里插入图片描述

二. 思想

2.1 算法—回溯算法

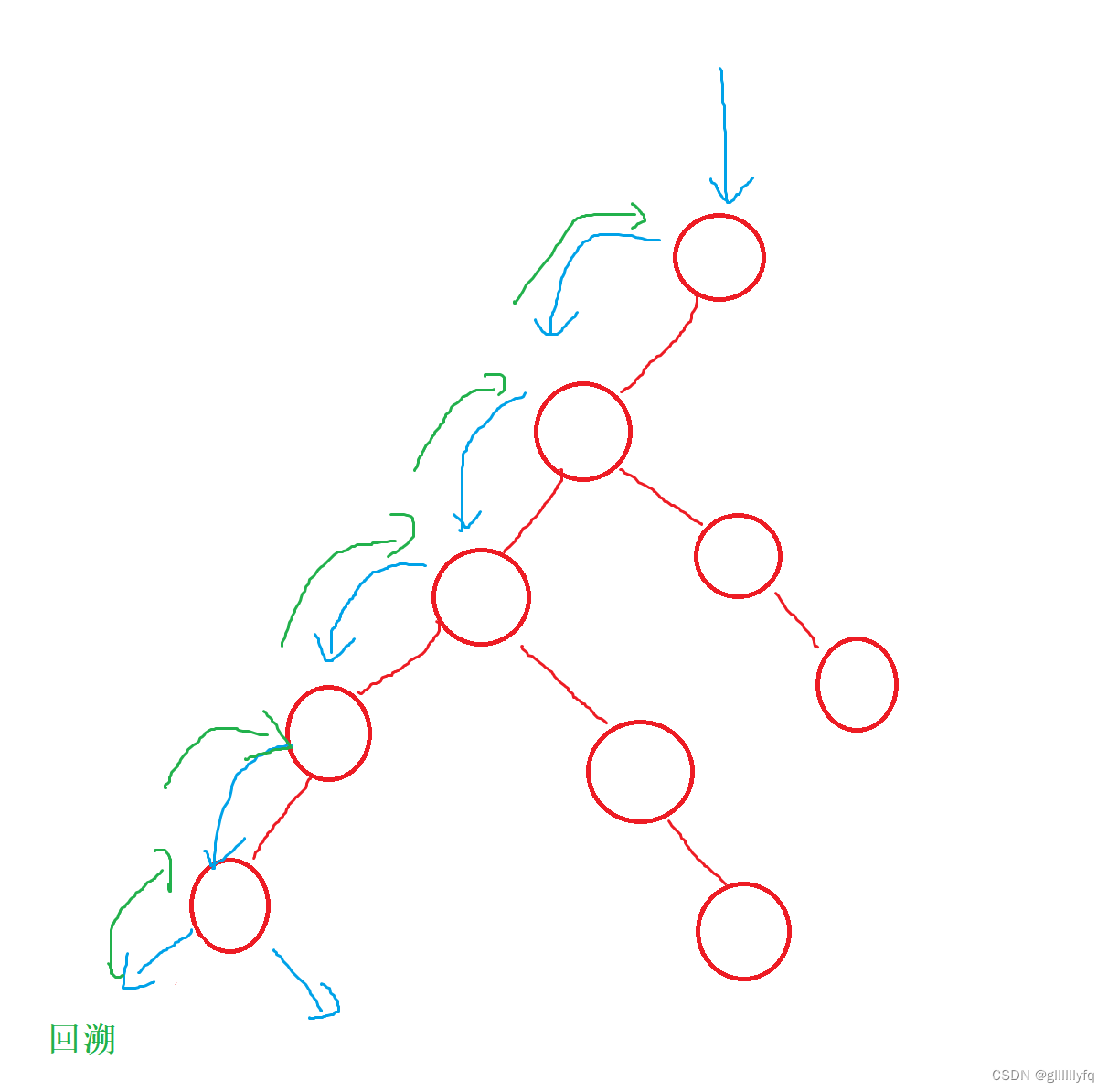
  • 回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

  • 回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

  • 许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。（深度优先遍历，能走则走，不能走则退）
    在这里插入图片描述

2.2 思路分析+图解

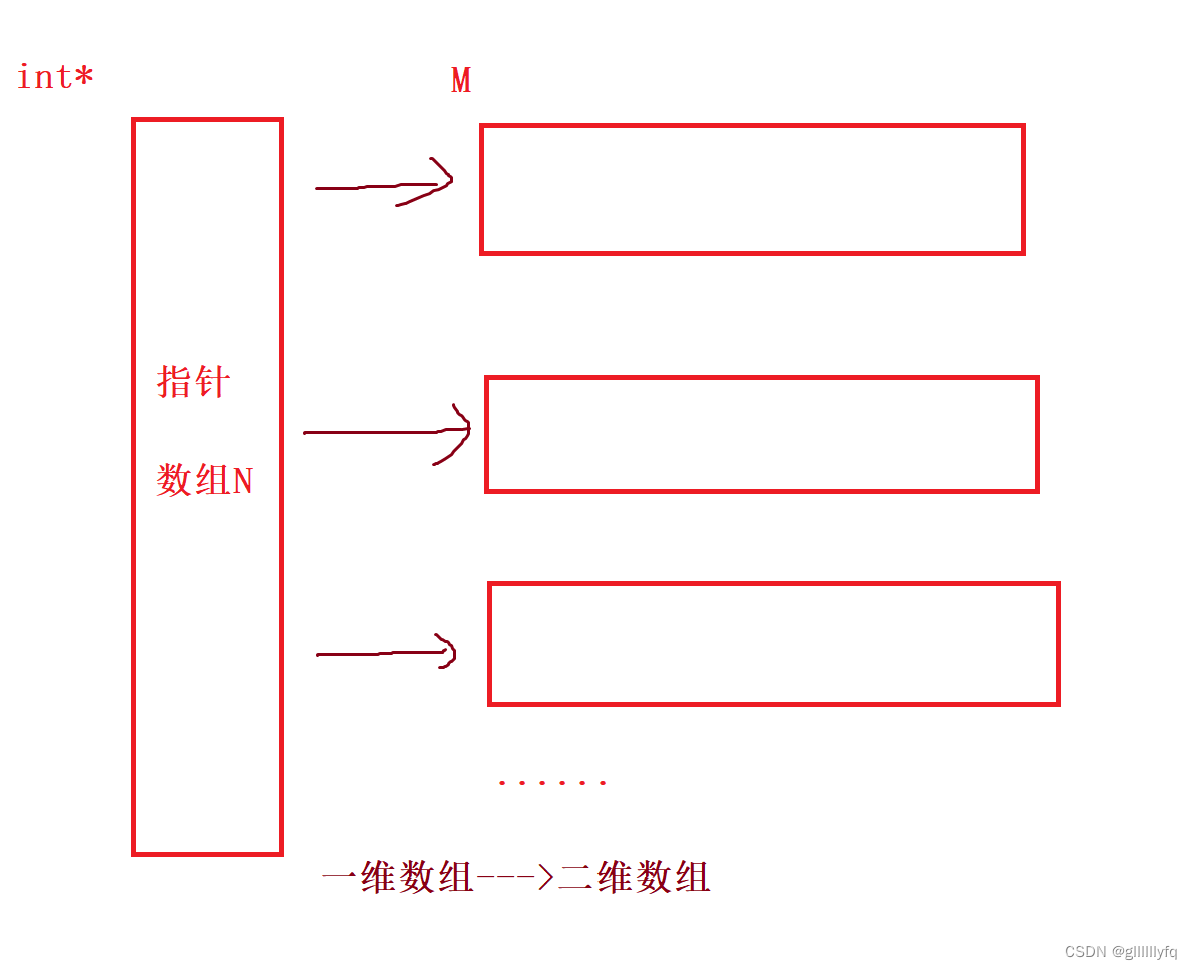
  • 对于不支持变长数组的C版本来说，如果需要实现二维变长数组的话，就需要动态开辟二维数组。

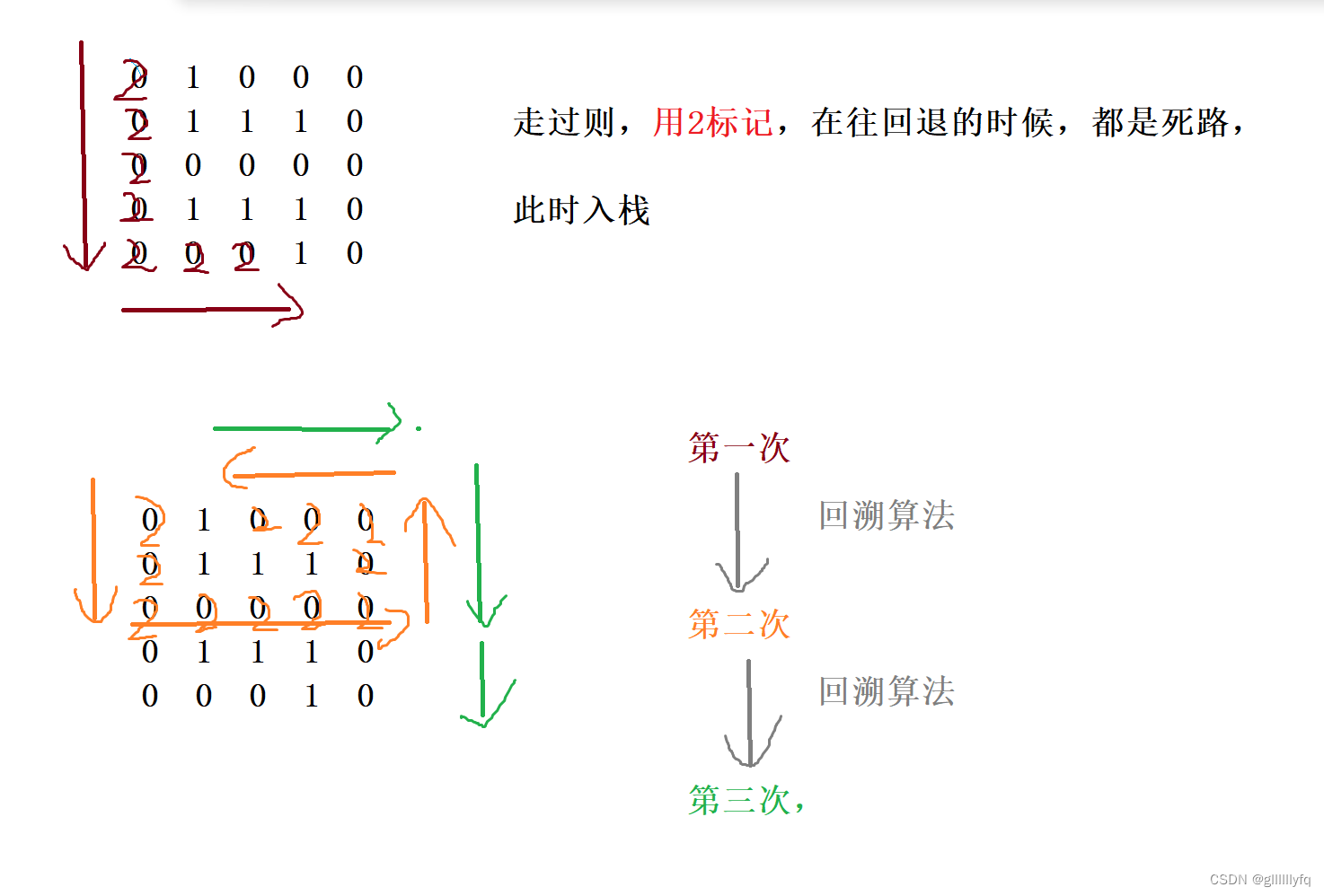
  • 每次需要对上下左右四个方向进行判断（但是四个方向选择的先后顺序不是很重要，每个迷宫不一样），才能到达下一个坐标，并且如果四个方向都不能走而且还没到达终点，那么就要往回走。

  • 为了判断往回是否还有其它能走的方向，我们需要对走过的坐标进行标记（已走过的坐标，用数字 2 标记），这样就不会出现走重复的路线。

  • 在结束的时候，我们需要打印这条路径的每个坐标，那么我们就需要对我们走过的坐标进行储存，对到达不了终点的路上的坐标消除，所以似乎需要栈来帮我们储存这个坐标。

在这里插入图片描述

三. 代码实现

3.1 二维数组的实现

在这里插入图片描述

void PrintMase(int** mase, int N, int M)
{
	for (int i = 0;i < N;i++)//先确定行---一维数组
	{
		for (int j = 0;j < M;j++)
		{
			printf("%d ", mase[i][j]);
		}
		printf("\n");
	}
}

3.2 上下左右四个方向的判断

  • 从（0，0）坐标开始，假设先判断上下，再判断左右，如果能通过就移动坐标，并且进入下次判断，直到到达终点，或者不能移动，并且需要对每次到达的坐标进行标记，假设标记为2。

  • 如果四个方向都不能走，并且没到达终点，那么将一直返回上一个位置，直到有其它方向能走。

  • 如果到达终点，返回true，直到跳出所有递归。

bool GetMasePath(int** maze, int N, int M)
{
	StackPush(&path, cur);//cur表示当前坐标
	if (cur.row == N - 1 && cur.col == M - 1)//当前坐标为右下时，走出迷宫
	{
		return true;
	}

	//走过的标志为2
	PT next;
	maze[cur, row][cur.col] == 2;

	//上
	next = cur;
	next.row -= 1;//行减1
	if (IsPass(mzse, N, M, next))
	{
		if (GetMasePath(maze, N, M, next))
		{
			return true;
		}
	}

	//下
	next = cur;
	next.row += 1;//行加1
	if (IsPass(mzse, N, M, next))
	{
		if (GetMasePath(maze, N, M, next))
		{
			return true;
		}
	}

	//左
	next = cur;
	next.col -= 1;//列减1
	if (IsPass(mzse, N, M, next))
	{
		if (GetMasePath(maze, N, M, next))
		{
			return true;
		}
	}

	//右
	next = cur;
	next.col += 1;//列加1
	if (IsPass(mzse, N, M, next))
	{
		if (GetMasePath(maze, N, M, next))
		{
			return true;
		}
	}
}

3.4 用栈记录坐标的实现

由于C语言没有自己的栈，所以要自己搭建一个栈。

  • 每次判断坐标前，先将当前坐标存入栈中，如果四个方向都不能走的时候，再出栈。

  • 当到达终点，返回完后，对栈中数据进行处理。

  • 因为栈中数据打印后与题目要求的打印相反，所有需要再创建一个栈，将当前栈中的数据导入另一个栈中，从而实现相反的打印。

为什么要建立两个栈？

因为题目要求的打印路径顺序是有先后的，只有一个栈是，路径坐标是倒的，与题目要求相反；所以建立两个栈，使得坐标顺序不变

typedef PT STDataType;

typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;//空间
}ST;

void StackInit(ST* ps);
void StackDestory(ST* ps);

void StackPush(ST* ps, STDataType x);//入栈
void StackPop(ST* ps);//出栈

STDataType StackTop(ST* ps);//返回栈顶元素

int StackSize(ST* ps);//栈大小

bool StackEmpty(ST* ps);//bool 判断是否栈空，栈空为1


//初始化
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);//初次分配
	if (ps->a == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	ps->capacity = 4;
	ps->top = 0;
}



//销毁栈
void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}



//入栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	if (ps->top == ps->capacity)
	{
		STDataType* tmp = (STDataType)realloc(ps->a, ps->capacity);//再分配
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);//为假，退出
		}
		else
		{
			ps->a = tmp;
			ps->capacity *= 2;
		}
	}
	ps->a[ps->top] = x;
	ps->top++;

}



//出栈
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);

	ps->top--;
}



//返回栈顶
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	{
		return ps->a[ps->top - 1];
	}
}



//栈大小
int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

//判断栈空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

Stack path;
/

//打印迷宫
void PrintMase(int** mase, int N, int M)
{
	for (int i = 0;i < N;i++)//先确定行---一维数组
	{
		for (int j = 0;j < M;j++)
		{
			printf("%d ", mase[i][j]);
		}
		printf("\n");
	}
}


//输出栈中坐标路径
void PrintPath(Stack* ps)
{
	//把path数据倒置入rPath
	Stack rPath;
	StackInit(&rPath);
	while (!StackEmpty(&Path)
	{
		StackPush(&rPath, StackTop(&Path));
		StackPop(&path)
	}
	while (!StackEmpty(&rPath)
	{
		PT top = StackTop(&rPath);
		printf("(%d , %d)\n", top.row, top.col);
		StackPop(&rpath)
	}
}

//判读路径是否正确
bool IsPass(int** maze, int N, int M)
{
	if (pos.row >= 0 && pos.row < N && pos.col >= 0 
		&& pos.col < M 
		&& masz[pos.row][pos.col] == 0)
	{
		return true;
	}
	else
	{
		return false;
	}
}

3.5 完整代码

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>

typedef struct Postion
{
	int row;
	int col;
}PT;
//

typedef PT STDataType;

typedef struct Stack
{
	STDataType* a;
	int top;
	int capacity;//空间
}ST;

void StackInit(ST* ps);
void StackDestory(ST* ps);

void StackPush(ST* ps, STDataType x);//入栈
void StackPop(ST* ps);//出栈

STDataType StackTop(ST* ps);//返回栈顶元素

int StackSize(ST* ps);//栈大小

bool StackEmpty(ST* ps);//bool 判断是否栈空，栈空为1

//初始化
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = (STDataType*)malloc(sizeof(STDataType) * 4);//初次分配
	if (ps->a == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	ps->capacity = 4;
	ps->top = 0;
}

//销毁栈
void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->top = ps->capacity = 0;
}

//入栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	if (ps->top == ps->capacity)
	{
		STDataType* tmp = (STDataType)realloc(ps->a, ps->capacity);//再分配
		if (tmp == NULL)
		{
			printf("realloc fail\n");
			exit(-1);//为假，退出
		}
		else
		{
			ps->a = tmp;
			ps->capacity *= 2;
		}
	}
	ps->a[ps->top] = x;
	ps->top++;

}

//出栈
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);

	ps->top--;
}

//返回栈顶
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	{
		return ps->a[ps->top - 1];
	}
}

//栈大小
int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

//判断栈空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

Stack path;
/

//打印迷宫
void PrintMase(int** mase, int N, int M)
{
	for (int i = 0;i < N;i++)//先确定行---一维数组
	{
		for (int j = 0;j < M;j++)
		{
			printf("%d ", mase[i][j]);
		}
		printf("\n");
	}
}

//输出栈中坐标路径
void PrintPath(Stack* ps)
{
	//把path数据倒置入rPath
	Stack rPath;
	StackInit(&rPath);
	while (!StackEmpty(&Path)
	{
		StackPush(&rPath, StackTop(&Path));
		StackPop(&path)
	}
	while (!StackEmpty(&rPath)
	{
		PT top = StackTop(&rPath);
		printf("(%d , %d)\n", top.row, top.col);
		StackPop(&rpath)
	}
}

//判读路径是否正确
bool IsPass(int** maze, int N, int M)
{
	if (pos.row >= 0 && pos.row < N && pos.col >= 0 
		&& pos.col < M 
		&& masz[pos.row][pos.col] == 0)
	{
		return true;
	}
	else
	{
		return false;
	}
}

//上下左右遍历
bool GetMasePath(int** maze, int N, int M)
{
	StackPush(&path, cur);//cur表示当前坐标
	if (cur.row == N - 1 && cur.col == M - 1)//当前坐标为右下时，走出迷宫
	{
		return true;
	}

	//走过的标志为2
	PT next;
	maze[cur, row][cur.col] == 2;

	//上
	next = cur;
	next.row -= 1;//行减1
	if (IsPass(mzse, N, M, next))
	{
		if (GetMasePath(maze, N, M, next))
		{
			return true;
		}
	}

	//下
	next = cur;
	next.row += 1;//行加1
	if (IsPass(mzse, N, M, next))
	{
		if (GetMasePath(maze, N, M, next))
		{
			return true;
		}
	}

	//左
	next = cur;
	next.col -= 1;//列减1
	if (IsPass(mzse, N, M, next))
	{
		if (GetMasePath(maze, N, M, next))
		{
			return true;
		}
	}

	//右
	next = cur;
	next.col += 1;//列加1
	if (IsPass(mzse, N, M, next))
	{
		if (GetMasePath(maze, N, M, next))
		{
			return true;
		}
	}
}

int main()
{
	int N = 0, M = 0;
	while (scanf("%d%d", &N, &M) != EOF)
	{
		// int a[n][m]; // vs2013 不支持
		// 动态开辟二维数组
		int** maze = (int**)malloc(sizeof(int*) * N);
		for (int i = 0; i < N; ++i)
		{
			maze[i] = (int*)malloc(sizeof(int) * M);
		}

		// 二维数组得输入
		for (int i = 0; i < N; ++i)
		{
			for (int j = 0; j < M; ++j)
			{
				scanf("%d", &maze[i][j]);
			}
		}

		StackInit(&path);
		// PrintMaze(maze, N, M);
		PT entry = { 0, 0 };
		if (GetMazePath(maze, N, M, entry))
		{
			//printf("找到通路\n");
			PirntPath(&path);
		}
		else
		{
			printf("没有找到通路\n");
		}

		StackDestory(&path);

		for (int i = 0; i < N; ++i)
		{
			free(maze[i]);
		}
		free(maze);
		maze = NULL;
	}

	return 0;
}

四. 总结

迷宫问题的难点:

  1. 建立两个栈，使得打印的顺序是正确的
  2. 怎么找路径，标记已经走过的坐标
  3. 栈的应用
  4. 递归
  5. 回溯算法

感谢阅读！


http://www.kler.cn/a/10519.html

相关文章：

  • ELK-Logstash配置
  • 攻防世界37-unseping-CTFWeb
  • 03WIFI与蓝牙1——基于全志V3S的Linux开发板教程笔记
  • uniapp(API-Promise 化)
  • js.零钱兑换
  • 图像融合self
  • CLIP：语言-图像表示之间的桥梁
  • Arcgis Engine之打开MXD文档
  • Linux less 命令
  • SpringBoot ElasticSearch 【SpringBoot系列16】
  • 归排、计排深度理解
  • docker运行服务端性能监控系统Prometheus和数据分析系统Grafana
  • 智慧校园大数据云平台（4）
  • 2023.04.16 学习周报
  • Java学习
  • 【数据结构】解析队列各接口功能实现
  • JS实用技巧断点调试详解
  • 一、docker-技术架构
  • C++ Primer阅读笔记--标准库类型string和vector的使用
  • oracle中sql 正则怎么写？
  • ArrayList的深入理解
  • 不会注册ChatGPT?4个国内网站让你尽情体验
  • GameFramework 框架详解之 如何接入热更框架HybridCLR
  • 【音频处理】创建环绕声混响
  • pycharm笔记
  • 内部人员或给企业造成毁灭性损失