Java——矩形覆盖
题目链接
牛客在线oj题——矩形覆盖
题目描述
我们可以用 21 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 21 的小矩形无重叠地覆盖一个 2*n 的大矩形,从同一个方向看总共有多少种不同的方法?
数据范围:0≤n≤38
进阶:空间复杂度 O(1) ,时间复杂度 O(n)
注意:约定 n == 0 时,输出 0
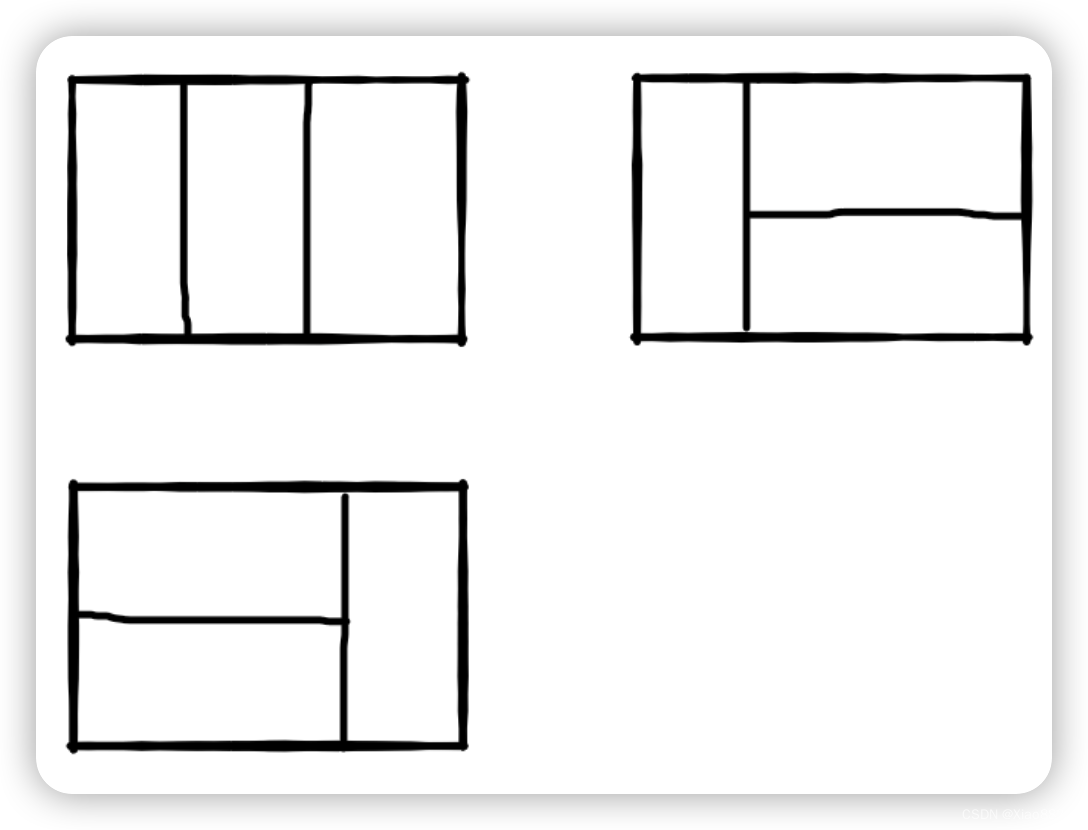
比如n=3时,2*3的矩形块有3种不同的覆盖方法(从同一个方向看):
输入描述:
2*1的小矩形的总个数n
返回值描述:
覆盖一个2*n的大矩形总共有多少种不同的方法(从同一个方向看)
题目示例
示例1
输入:
0
返回值:
0
示例2
输入:
1
返回值:
1
示例3
输入:
4
返回值:
5
解题思路
根据题目描述
当n = 0时,答案是0,当n = 1时,答案是1,当n = 2时,答案是2,当n = 3时,答案是3
我们可以继续列举一下接下来的情况,找一下其中的规律
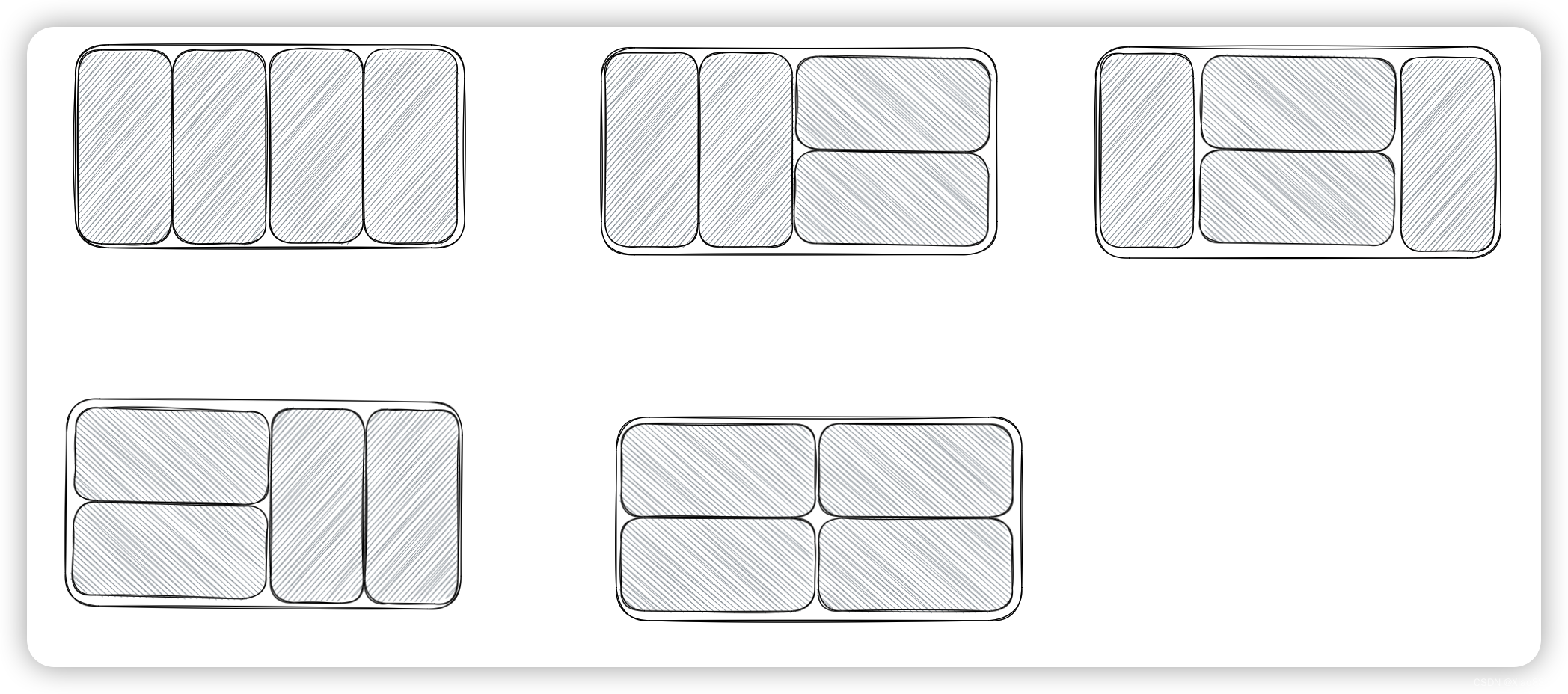
当n = 4时,有五种覆盖方法
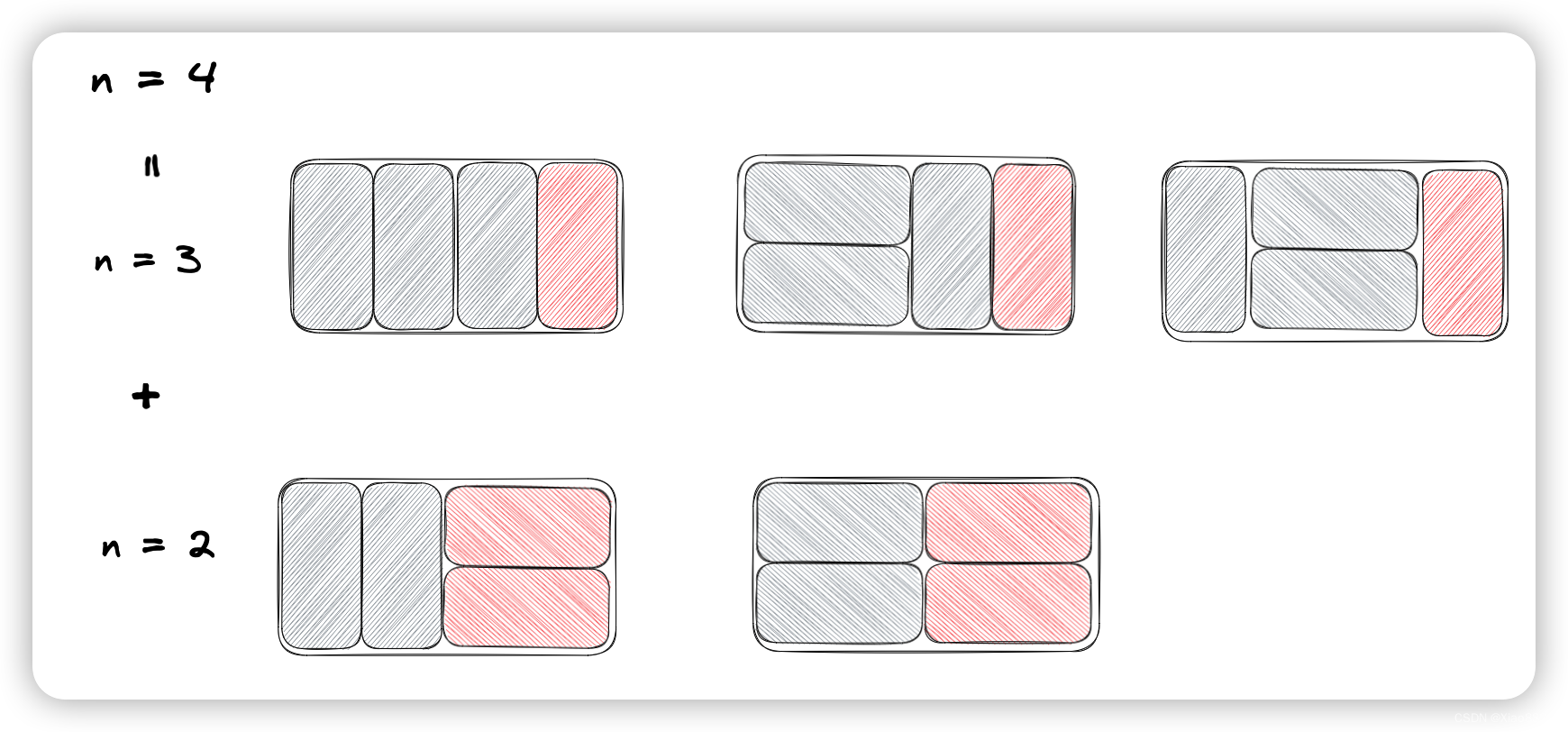
可以看出,其中输入的n与输出的方法数的规律是f(n) = f(n - 1) + f(n - 2) (当n大于等于2)
这是因为,覆盖2 * n的矩阵可以通过2 * (n - 1)的矩阵直接放置一个竖型矩阵块得到,或者是2 * (n - 2)的矩阵直接放置两个横型矩阵块
完整代码
public class Solution {
public int rectCover(int target) {
if(target <= 2){
return target;
}
int[] arr = new int[target + 1];
arr[1] = 1;
arr[2] = 2;
for(int i = 3; i <= target; i++){
arr[i] = arr[i - 2] + arr[i - 1];
}
return arr[target];
}
}
