05 MIT线性代数-转置,置换,向量空间Transposes, permutations, spaces
1. Permutations P:
execute row exchanges
becomes PA = LU for any invertible A
Permutations P = identity matrix with reordered rows
m=n (n-1) ... (3) (2) (1) counts recordings, counts all nxn permuations
对于nxn矩阵存在着n!个置换矩阵
,
2. Transpose:

2.1 Symmetric matrices
对称矩阵
2.2 矩阵乘积的转置
2.3  is always symmetric
is always symmetric
why? take transpose
3. 向量空间 Vector spaces
向量空间对线性运算封闭,即空间内向量进行线性运算得到的向量仍在空间之内
example: = all 2-dim real vectors=x-y plane
first component, second component
= all vectors with 3 components
= all column vectors with m real components
所有向量空间必然包含零向量,因为任何向量数乘0或者加上反向量都会得到零向量,而因为向量空间对线性运算封闭,所以零向量必属于向量空间
反例 not a vector space:
中的第一象限则不是一个向量空间, 加法数乘不封闭
4. 子空间 Subspaces
a vector space inside , subspace of
line in through zero vector
反例:
中不穿过原点的直线就不是向量空间。子空间必须包含零向量,原因就是数乘0的到的零向量必须处于子空间中
subspaces of 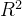 :
:
1. all of
2. any line through L(line)
3. zero vector only z(zero)
subspaces of 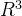 :
:
1. all of
2. any plane through P(plane)
2. any line through L(line)
3. zero vector only z(zero) =

5. 列空间 Column spaces
Columns in : all their combinations from a subspace called column space C(A)

空间内包含两向量的所有线性组合