当前位置：首页 > article >正文

【LeetCode每日一题合集】2023.10.16-2023.10.22（只出现一次的数字Ⅲ）

article 2024/11/15 14:05:25

文章目录

260. 只出现一次的数字 III⭐（异或）🐂
2652. 倍数求和
- 解法1——枚举模拟
- 解法2—— $O (1)$ 容斥原理
- 相似题目——1201. 丑数 III（二分查找+容斥原理）
2530. 执行 K 次操作后的最大分数
- 解法1——贪心+优先队列
- 解法2—— $O (1)$ 空间原地堆化
1726. 同积元组（哈希表+组合数学）
2525. 根据规则将箱子分类（按题意模拟，分类讨论）
2316. 统计无向图中无法互相到达点对数
- 解法1——并查集
- 解法2——dfs求连通块大小
1402. 做菜顺序
- 解法1——动态规划
- 解法2——贪心⭐

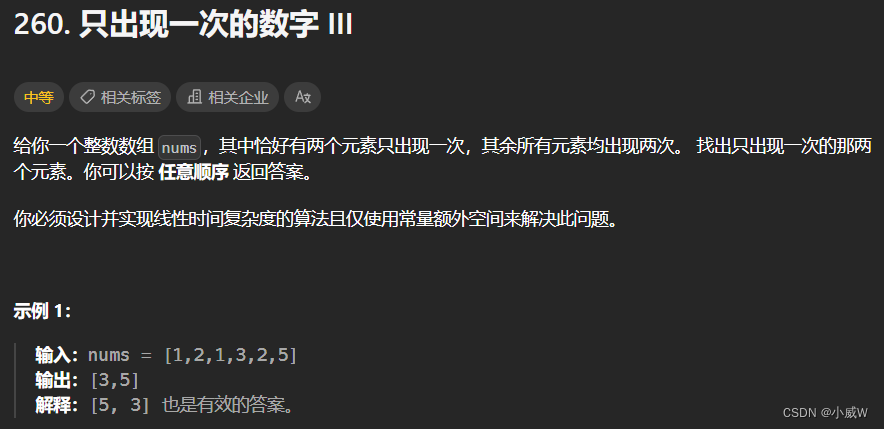
260. 只出现一次的数字 III⭐（异或）🐂

https://leetcode.cn/problems/single-number-iii/description/?envType=daily-question&envId=2023-10-16

在这里插入图片描述

提示：
2 <= nums.length <= 3 * 10^4
-2^31 <= nums[i] <= 2^31 - 1
除两个只出现一次的整数外，nums 中的其他数字都出现两次

类似分治的思想。
先将数组全部异或，得出的结果是两个只出现一次数字的异或结果。
其中一定有1，因为这两个数字不同。
取出其最低位的1作为判断标准对原数组分组（实际上任意位的1都可以），分成的两组分别包括这两个只出现一次的数字。
这样就把问题转换成了两个 136. 只出现一次的数字

class Solution {
    public int[] singleNumber(int[] nums) {
        int xor = 0;
        for (int num: nums) xor ^= num;
        int mask = xor & (-xor);    // 获取最低位的1
        int[] ans = new int[2];
        for (int num: nums) {
            if ((num & mask) == 0) ans[0] ^= num;
            else ans[1] ^= num;
        }
        return ans;
    }
}

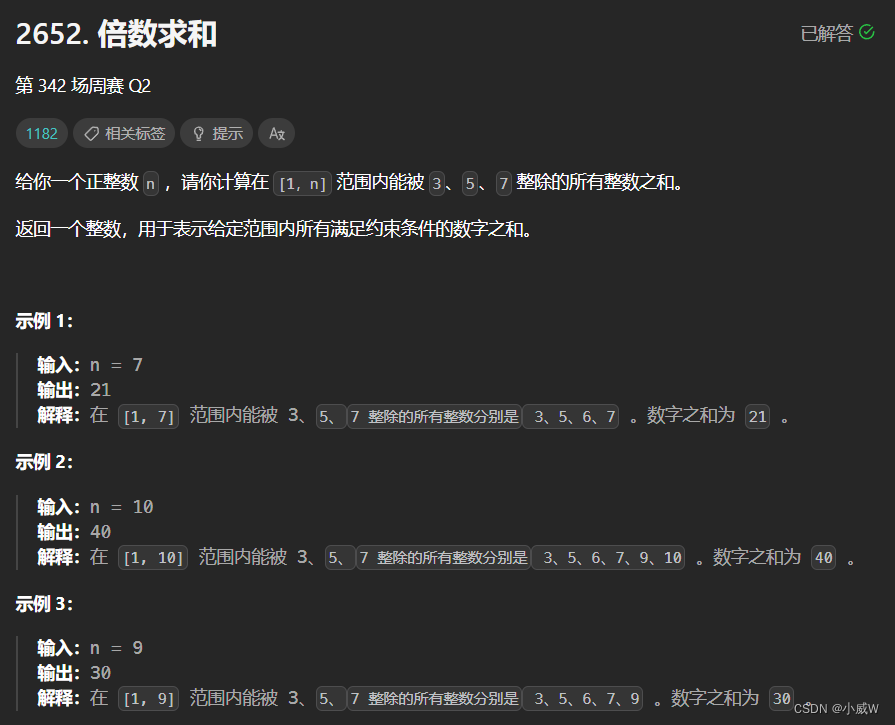
2652. 倍数求和

https://leetcode.cn/problems/sum-multiples/description/?envType=daily-question&envId=2023-10-17

在这里插入图片描述

提示：
1 <= n <= 10^3

解法1——枚举模拟

class Solution {
    public int sumOfMultiples(int n) {
        int ans = 0;
        for (int i = 1; i <= n; ++i) {
            if (i % 3 == 0 || i % 5 == 0 || i % 7 == 0) ans += i;
        }
        return ans;
    }
}

解法2—— $O (1)$ 容斥原理

class Solution {
    int n;
    public int sumOfMultiples(int n) {
        this.n = n;
        return s(3) + s(5) + s(7) - s(15) - s(21) - s(35) + s(105);
    }
    // 计算从x~(n/x)x，共n/x项
    public int s(int x) {
        return n / x * (x + n / x * x) / 2;
    }
}

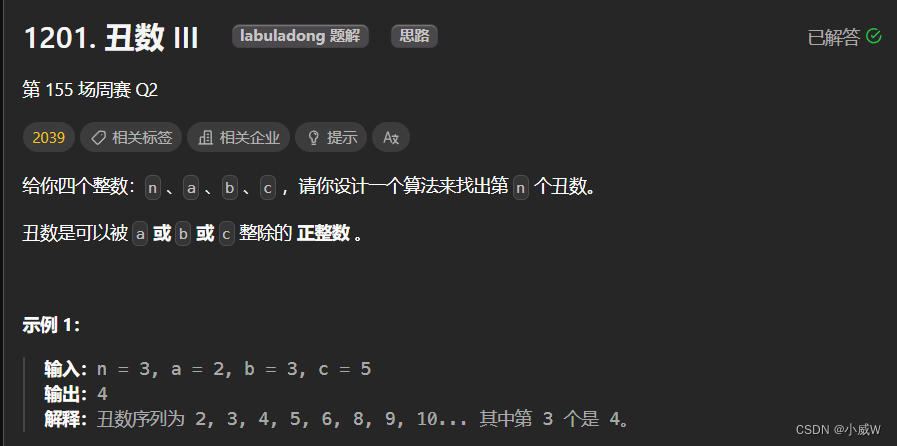
相似题目——1201. 丑数 III（二分查找+容斥原理）

https://leetcode.cn/problems/ugly-number-iii/description/

在这里插入图片描述
提示：
1 <= n, a, b, c <= 10^9
1 <= a * b * c <= 10^18
本题结果在 [1, 2 * 10^9] 的范围内

为什么会想到二分？
因为直接求答案不好求，但是我们可以判断1~x的范围内是否有n个丑数。

class Solution {
    public int nthUglyNumber(int n, int a, int b, int c) {
        long x = lcm(a, b), y = lcm(b, c), z = lcm(a, c), q = lcm(x, y);
        long l = 1, r = (long)2e9;
        while (l < r) {
            long mid = l + r >> 1;
            long aa = mid / a, bb = mid / b, cc = mid / c, xx = mid / x, yy = mid / y, zz = mid / z, qq = mid / q;
            long s = aa + bb + cc - xx - yy - zz + qq;
            if (s < n) l = mid + 1;
            else r = mid;
        }
        return (int)l;
    }

    public long gcd(long a, long b) {
        return b == 0? a: gcd(b, a % b);
    }

    public long lcm(long a, long b) {
        return a / gcd(a, b) * b;
    }
}

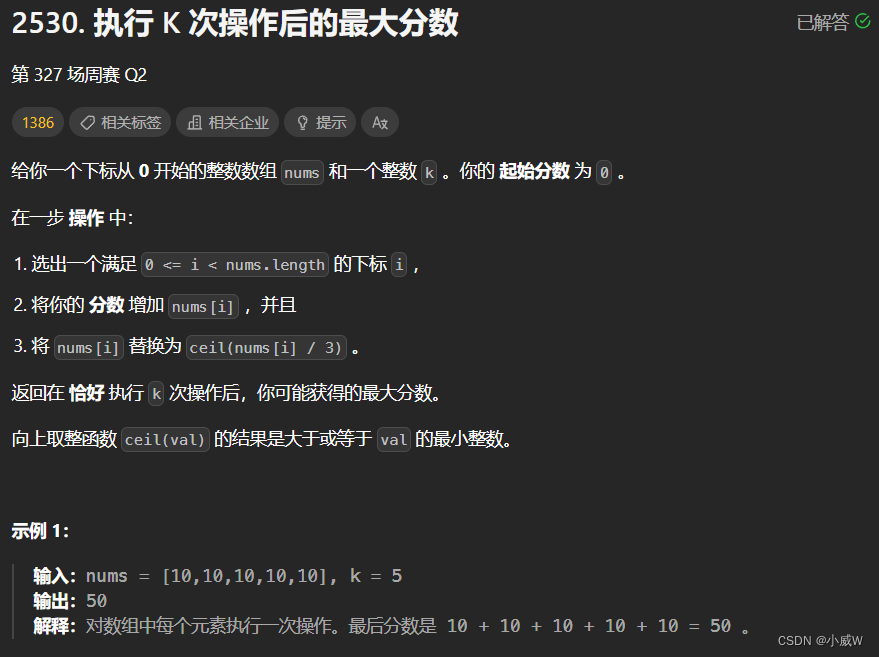
2530. 执行 K 次操作后的最大分数

https://leetcode.cn/problems/maximal-score-after-applying-k-operations/description/?envType=daily-question&envId=2023-10-18
在这里插入图片描述
提示：

1 <= nums.length, k <= 10^5
1 <= nums[i] <= 10^9

解法1——贪心+优先队列

每次增加最大的数字即可。

class Solution {
    public long maxKelements(int[] nums, int k) {
        long ans = 0;
        PriorityQueue<Integer> pq = new PriorityQueue<>((a, b) -> b - a);
        for (int num: nums) pq.offer(num);
        for (int i = 0; i < k; ++i) {
            int c = pq.poll();
            ans += c;
            pq.offer((c + 2) / 3);
        }
        return ans;
    }
}

解法2—— $O (1)$ 空间原地堆化

https://leetcode.cn/problems/maximal-score-after-applying-k-operations/solutions/2487446/o1-kong-jian-zuo-fa-pythonjavacgojsrust-ztx6f/?envType=daily-question&envId=2023-10-18

原地堆化，把 nums 数组当成一个堆。
从 h.length / 2 - 1 开始倒序下沉。

class Solution {
    public long maxKelements(int[] nums, int k) {
        heapify(nums);
        long ans = 0;
        while (k-- > 0) {
            ans += nums[0];
            nums[0] = (nums[0] + 2) / 3;
            sink(nums, 0);      // 下沉
        }
        return ans;
    }

    // 保证h[0]>=max(h[2*i+1],h[2*i+2])
    public void heapify(int[] h) {
        for (int i = h.length / 2 - 1; i >= 0; --i) {
            sink(h, i);
        }
    }

    public void sink(int[] h, int i) {
        int n = h.length;
        while (2 * i + 1 < n) {
            // 挑选左右儿子中更大的和i交换
            int j = 2 * i + 1;          // i的左儿子
            if (j + 1 < n && h[j + 1] > h[j]) j++;
            if (h[j] <= h[i]) break;    // 停止下沉
            swap(h, i, j);
            i = j;
        }
    }

    public void swap(int[] h, int i, int j) {
        int tmp = h[i];
        h[i] = h[j];
        h[j] = tmp;
    }
}

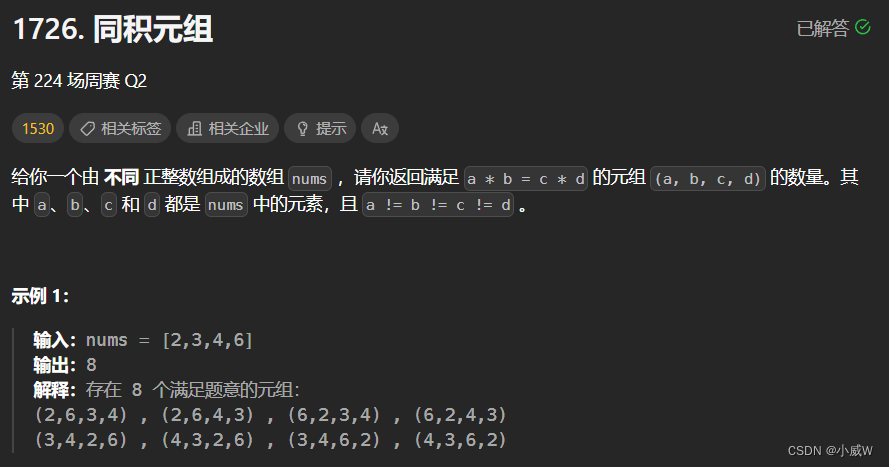
1726. 同积元组（哈希表+组合数学）

https://leetcode.cn/problems/tuple-with-same-product/description/
在这里插入图片描述

提示：

1 <= nums.length <= 1000
1 <= nums[i] <= 10^4
nums 中的所有元素互不相同

计算出数组中所有两两组合的乘积的各个数量。
那么各个成绩的组合数就是 $C_x^2=x*(x-1)$ ，即任选两组。每种组合4个数字可以任意排位置，最后结果*4。

class Solution {
    public int tupleSameProduct(int[] nums) {
        int n = nums.length, ans = 0;
        Map<Integer, Integer> cnt = new HashMap<>();
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                cnt.merge(nums[i] * nums[j], 1, Integer::sum);
            }
        }
        for (int v: cnt.values()) {
            if (v > 1) ans += v * (v - 1);
        }
        return ans * 4;
    }
}

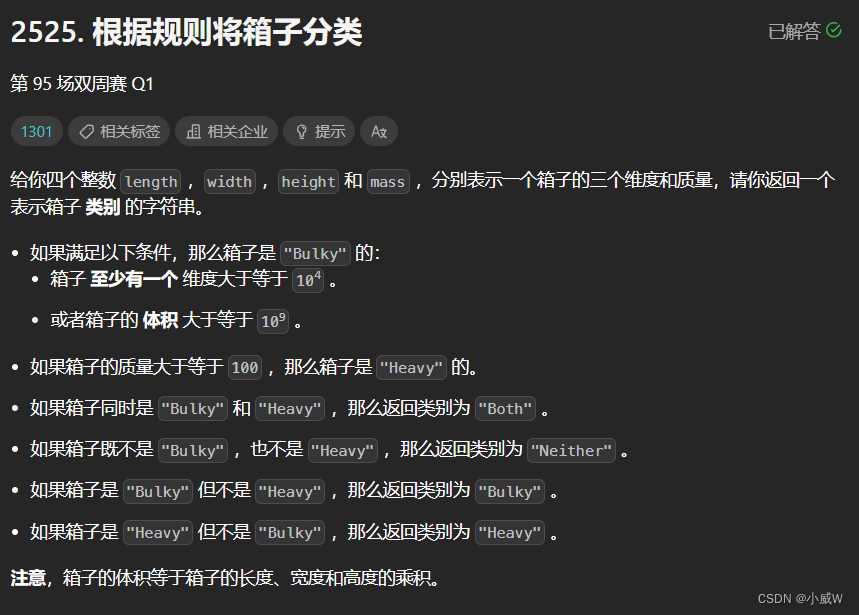
2525. 根据规则将箱子分类（按题意模拟，分类讨论）

https://leetcode.cn/problems/categorize-box-according-to-criteria/description/?envType=daily-question&envId=2023-10-20

在这里插入图片描述
提示：

1 <= length, width, height <= 10^5
1 <= mass <= 10^3

class Solution {
    public String categorizeBox(int length, int width, int height, int mass) {
        boolean bulky = false, heavy = false;
        if (length >= 10000 || width >= 10000 || height >= 10000 || mass >= 10000 || (long)length * width * height >= 1000000000) bulky = true;
        if (mass >= 100) heavy = true; 
        if (bulky && heavy) return "Both";
        if (!bulky && !heavy) return "Neither";
        if (bulky) return "Bulky";
        return "Heavy";
    }
}

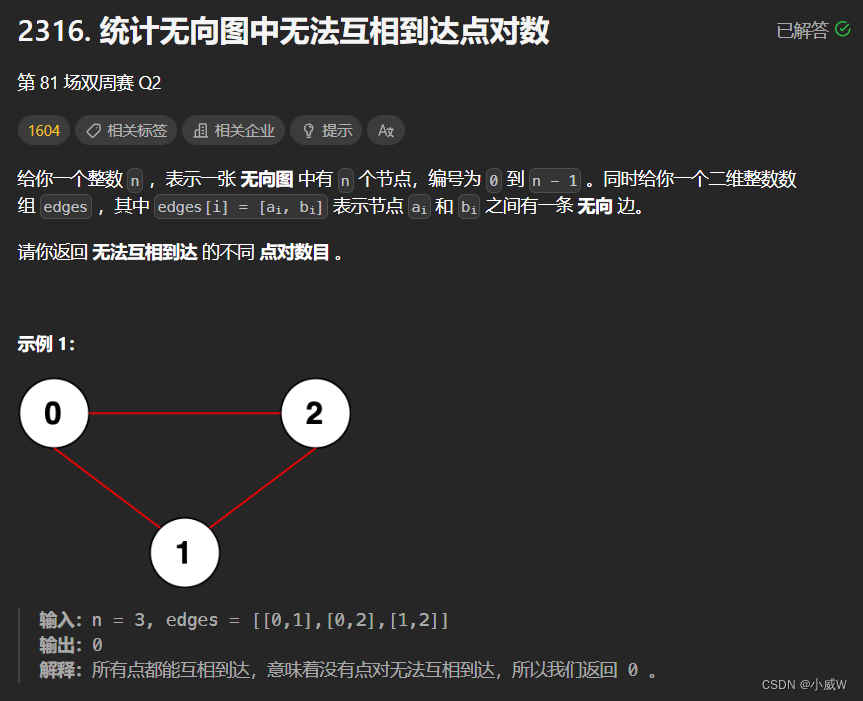
2316. 统计无向图中无法互相到达点对数

https://leetcode.cn/problems/count-unreachable-pairs-of-nodes-in-an-undirected-graph/description/?envType=daily-question&envId=2023-10-21

在这里插入图片描述

提示：

1 <= n <= 10^5
0 <= edges.length <= 2 * 10^5
edges[i].length == 2
0 <= ai, bi < n
ai != bi
不会有重复边。

解法1——并查集

关于并查集可见：【算法基础：数据结构】2.3 并查集

并查集得出各个联通集合中元素的数量，不同集合中的元素都可以两两组合。

class Solution {
    public long countPairs(int n, int[][] edges) {
        long ans = 0;
        // 并查集
        int[] p = new int[n];
        Arrays.setAll(p, e -> e);
        for (int[] e: edges) {
            if (p[e[0]] != p[e[1]]) p[find(p, e[0])] = find(p, e[1]);
        }
        // 记录每个集合中的元素个数
        Map<Integer, Integer> cnt = new HashMap<>();
        for (int i = 0; i < n; ++i) {
            cnt.merge(find(p, i), 1, Integer::sum);
        }
        for (int v: cnt.values()) {
            ans += (long)v * (n - v);       // 和其它所有集合的一一对应
        }
        return ans / 2;                     // 结果除以2去掉重复计算的
    }

    public int find(int[]p, int x) {
        if (p[x] != x) p[x] = find(p, p[x]);
        return p[x];
    }
}

解法2——dfs求连通块大小

class Solution {
    public long countPairs(int n, int[][] edges) {
        long ans = 0, total = 0;
        List<Integer>[] g = new ArrayList[n];
        boolean[] st = new boolean[n];
        Arrays.setAll(g, e -> new ArrayList<Integer>());
        for (int[] e: edges) {
            g[e[0]].add(e[1]);
            g[e[1]].add(e[0]);
        }
        for (int i = 0; i < n; ++i) {
            if (!st[i]) {
                int cnt = dfs(g, st, i);    // dfs计算连通块大小
                ans += total * cnt;
                total += cnt;
            }
        }
        return ans;
    }

    public int dfs(List<Integer>[] g, boolean[] st, int x) {
        int res = 1;
        st[x] = true;
        for (int y: g[x]) {
            if (!st[y]) {
                res += dfs(g, st, y);
            }
        }
        return res;
    }
}

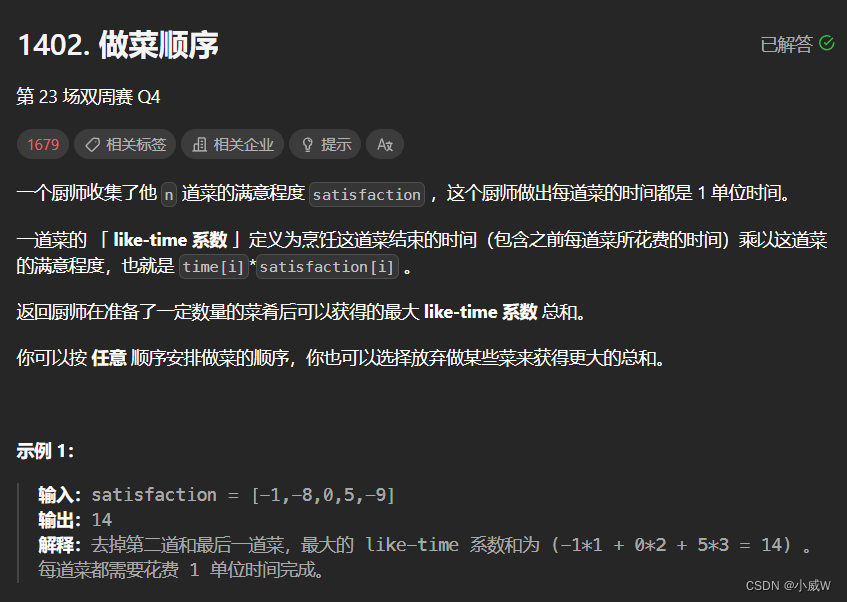
1402. 做菜顺序

https://leetcode.cn/problems/reducing-dishes/description/?envType=daily-question&envId=2023-10-22

在这里插入图片描述
提示：

n == satisfaction.length
1 <= n <= 500
-1000 <= satisfaction[i] <= 1000

解法1——动态规划

dp[i][j] 表示前 i+1 个菜，选择 j 个时的值。
最后结果是前 n 个菜中，选择 0~n 个时的最大值。

class Solution {
    public int maxSatisfaction(int[] satisfaction) {
        int n = satisfaction.length;
        int[][] dp = new int[n + 1][n + 1];
        Arrays.sort(satisfaction);
        dp[0][1] = satisfaction[0];
        for (int i = 1; i < n; ++i) {
            for (int j = 1; j <= i + 1; ++j) {
                dp[i][j] = dp[i - 1][j - 1] + satisfaction[i] * j;
            }
        }
        return Arrays.stream(dp[n - 1]).max().getAsInt();
    }
}

解法2——贪心⭐

见：https://leetcode.cn/problems/reducing-dishes/solutions/198214/zuo-cai-shun-xu-by-leetcode-solution/?envType=daily-question&envId=2023-10-22

class Solution {
    public int maxSatisfaction(int[] satisfaction) {
        Arrays.sort(satisfaction);
        int ans = 0, s = 0;
        for (int i = satisfaction.length - 1; i >= 0; --i) {
            s += satisfaction[i];
            if (s <= 0) return ans;
            ans += s;
        }
        return ans;
    }
}