当前位置：首页 > article >正文

【MATLAB源码-第59期】基于matlab的QPSK,16QAM164QAM等调制方式误码率对比，调制解调函数均是手动实现未调用内置函数。

article 2024/9/25 3:21:34

操作环境：

MATLAB 2022a

1、算法描述

正交幅度调制（QAM，Quadrature Amplitude Modulation）是一种在两个正交载波上进行幅度调制的调制方式。这两个载波通常是相位差为90度（π/2）的正弦波，因此被称作正交载波。这种调制方式因此而得名。

同其它调制方式类似，QAM通过载波某些参数的变化传输信息。在QAM中，数据信号由相互正交的两个载波的幅度变化表示。

模拟信号的相位调制和数字信号的PSK可以被认为是幅度不变、仅有相位变化的特殊的正交幅度调制。由此，模拟信号频率调制和数字信号FSK也可以被认为是相位调制（PSK）的特例，因为它们本质上就是相位调制。这里主要讨论数字信号的QAM，虽然模拟信号QAM也有很多应用，例如NTSC和PAL制式的电视系统就利用正交的载波传输不同的颜色分量。

类似于其他数字调制方式，QAM发射信号集可以用星座图方便地表示。星座图上每一个星座点对应发射信号集中的一个信号。设正交幅度调制的发射信号集大小为 N

，称之为N-QAM。星座点经常采用水平和垂直方向等间距的正方网格配置，当然也有其他的配置方式。数字通信中数据常采用二进制表示，这种情况下星座点的个数一般是2的幂。常见的QAM形式有16-QAM、64-QAM、256-QAM，以及未来5G采用之512－QAM及1024－QAM。星座点数越多，每个符号能传输的信息量就越大。但是，如果在星座图的平均能量保持不变的情况下增加星座点，会使星座点之间的距离变小，进而导致误码率上升。因此高阶星座图的可靠性比低阶要差。

当对数据传输速率的要求高过8-PSK能提供的上限时，一般采用QAM的调制方式。因为QAM的星座点比PSK的星座点更分散，星座点之间的距离因之更大，所以能提供更好的传输性能。但是QAM星座点的幅度不是完全相同的，所以它的解调器需要能同时正确检测相位和幅度，不像PSK解调只需要检测相位，这增加了QAM解调器的复杂性。

2、仿真结果演示

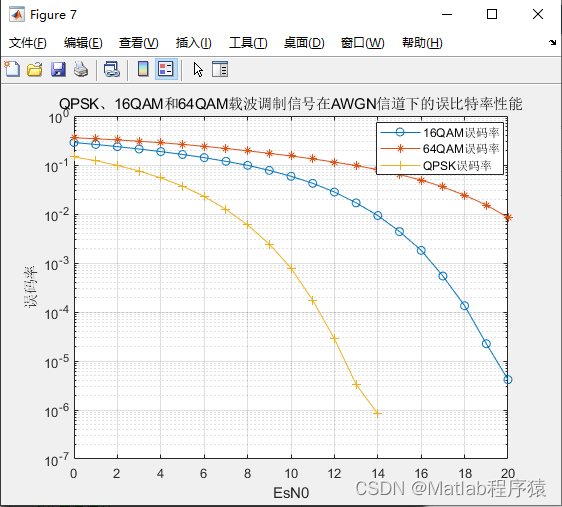
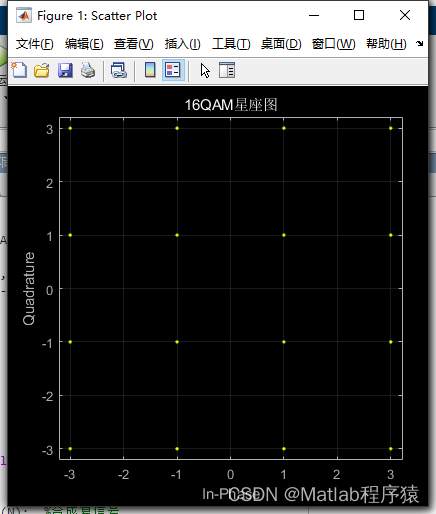
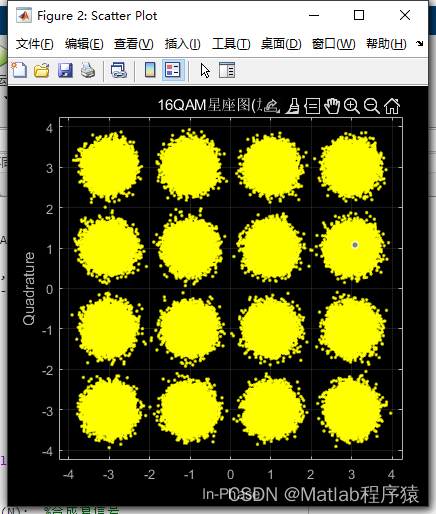
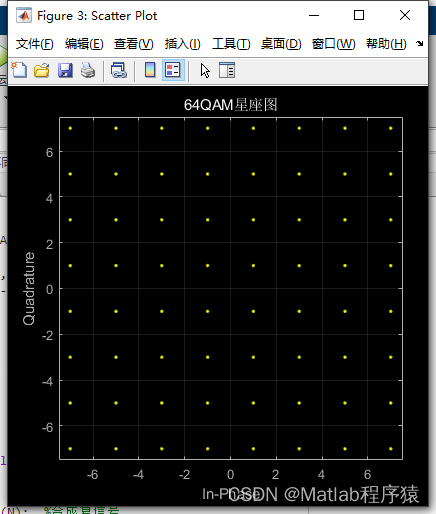
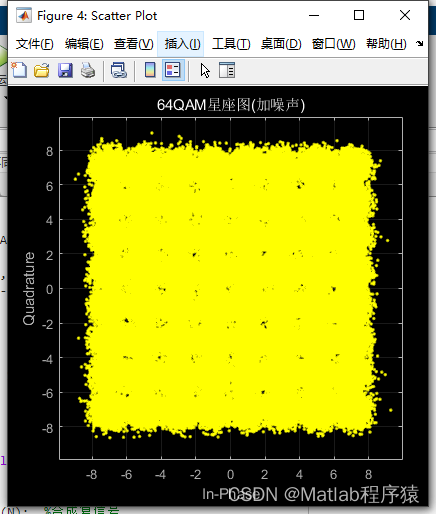
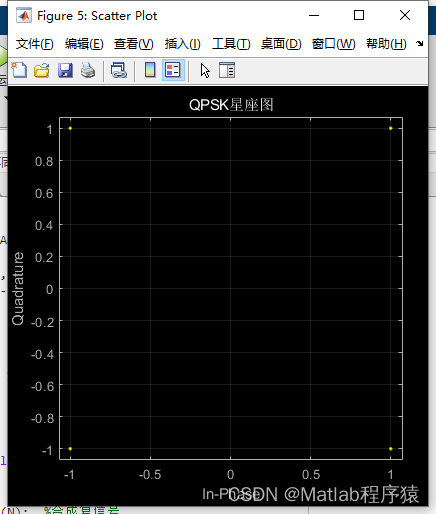
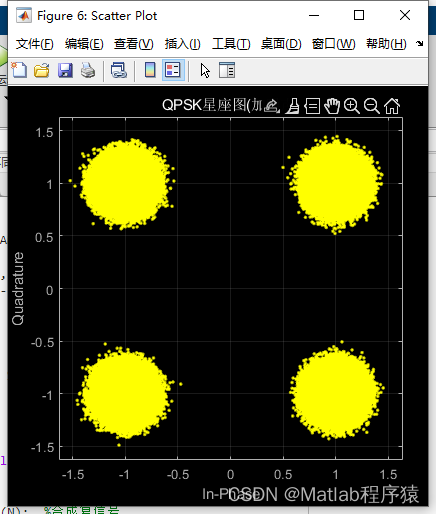
3、关键代码展示

%此段代码实现信号的64QAM调制

function [tx_64QAM]=  Mapping_64QAM (tx_bits)
 
global ac;%同相分量
global as;%正交分量
global num;

[m,n]=size(tx_bits);
num=m*n;

%同相分量：横坐标
map1=[-7,-7,-7,-7,-7,-7,-7,-7,-5,-5,-5,-5,-5,-5,-5,-5  -1,-1,-1,-1,-1,-1,-1,-1, -3   -3  -3  -3  -3  -3  -3  -3  7   7     7     7     7     7     7     7  5     5     5     5     5     5     5     5   1     1     1     1     1     1     1     1    3     3     3     3     3     3     3     3];

%正交分量：纵坐标
 map2=[-7 -5 -1 -3 7 5 1 3 -7 -5 -1 -3 7 5 1 3 -7 -5 -1 -3 7 5 1 3 -7 -5 -1 -3 7 5 1 3 -7 -5 -1 -3 7 5 1 3 -7 -5 -1 -3 7 5 1 3 -7 -5 -1 -3 7 5 1 3 -7 -5 -1 -3 7 5 1 3];


Dec_ac=zeros(num/6,1);
Dec_as=zeros(num/6,1);
 
ac=zeros(num/6,1);
as=zeros(num/6,1);
 
tx_64QAM=zeros(num/6,1);
 
for N=1:num/6
    Dec_ac(N,:)=bi2de(tx_bits(N,:),'left-msb');    
    Dec_as(N,:)=bi2de(tx_bits(N,:),'left-msb');  
    %同相分量ac
    ac(N)=map1(Dec_ac(N)+1);%MATLAB索引从1开始
    %正交分量as
    as(N)=map2(Dec_as(N)+1);%MATLAB索引从1开始  
    tx_64QAM(N,1)=ac(N)+1j*as(N);
end
debug=1;