List 3.5 详解原码、反码、补码
前言
欢迎来到我的博客,我是雨空集(全网同名),无论你是无意中发现我,还是有意搜索而来,我都感到荣幸。这里是一个分享知识、交流想法的平台,我希望我的博客能给你带来帮助和启发。如果你喜欢我的文章,别忘了收藏、点赞、关注,以便获取最新的内容。你还可以在文章下方留下你的想法和反馈,我非常欢迎你的意见。我会继续努力提供优质的内容。期待与你一起分享知识、互相学习,并建立一个积极的社区。让我们一起在这个知识之旅中取得进步!

本博客文章已收录至我的Java SE专栏,如需阅读其他有关博客笔记请转至该专栏下
传送门 -->Java SE_程序员雨空集
原码
原码:十进制数据的二进制表现形式,最左边是符号位,0为正,1为负
利用原码对正数进行计算是不会有问题的。
十进制是逢十进一,不会出现10这个数字。
二进制是逢二进一,不会出现2这个数字。
原码的示例
比如十进制56转成二进制就是00111000。
00111000中,最左边的0就是代表这个数为正数,其余的0111000代表56,也就是下面这个样子。

其中,一个0或者一个1就代码1bit(中文翻译叫比特位)。
计算机里是通常是把8个bit分为一组,叫做一个byte(字节),而字节是计算机中最小的存储单元。
而一个字节最大值表示为01111111,转化成十进制就是+127,是正的127。
最左边的符号位取0,其余位为数据,因为是求最大,每位上全部取最大为1。
而一个字节最小值表示为11111111,转化成十进制就是-127,是负的127。
最左边的符号位取1,其余位为数据,因为是求最小,每位上全部取最小也为1 。
原码的弊端
又举个例子
现在有一个字节代表的数是-0,也就是0,如下图
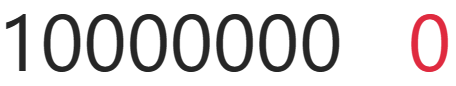
如果我现在要对它进行+1操作,也就是下面这样

按理说0+1=(+1),但是根据上图,这样做的话就粗问题了,按照二进制的规则,这样操作的二进制转成十进制为-1,也就是下图才是我们想要的结果

如果在此实际值上再进行+1操作,又出现了下面的情况

为什么会出现这样的情况呢?

想要理解清楚,需要结合数轴去理解
如果我要用二进制表示0的基础上+1,但是因为符号位是1代表负数,实际是在0的位置上往负的方向前进的1单位,如下图所示
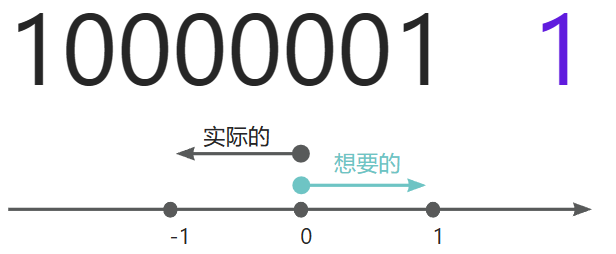
所以这就是原码的弊端:在原码的基础上,如果是负数计算,结果就出错,实际运算的结果,跟我们预期的结果是相反的。

如果我们结合上面的数轴,在进行负数计算的时候,如果把数轴的方向倒转一下,那不就得到了我们想要的结果了吗?因此,这就引出了反码的由来
反码
反码:为了解决原码不能计算负数的问题而出现的
计算规则:
- 正数的反码不变。
- 负数的反码在原码的基础上,符号位不变。数值取反,0变1,1变0。
为什么正数的反码不变?
- 因为正数之间的计算是没有任何问题,只有我们上面举到的例子中有负数的计算才会有反码的出现
反码的示例
又又举个栗子
十进制-56的二进制原码是10111000。根据规则,符号位不变。数值取反,0变1,1变0。它的反码为11000111
验证反码能不能解决原码负数计算的问题,我们可以验证一下
就看看-56+1的值是不是为-55的这个情况?
- -56的原码是10111000,而-56的反码就是11000111。
- 进行-56+1的操作就是在-56的反码11000111从最右边的数字进1位根据二进制逢二进一变为11001000
- 而55的原码是0011011,所以-55的原码就是1011011,所以-55的反码就是1100100,结果成立!

这么一来,你就懂了吧?如果还没明白,把上面的步骤多看几遍,你就懂了
反码的弊端
又又又举个例子,我现在
现在又一个十进制数字-2,其原码是1000 0010,其反码为1111 1101
- 如果对-2进行+1操作之后,其原码变为1000 0001,反码变为1111 1110,结果为-2+1=-1,没问题
- 如果对-2进行+2操作,也就是两次+1操作,原码会变成1000 0000 ,反码变为1111 1111,结果为-2+2=0 也没问题
- 如果对-2进行+3进行操作,也就是三次+1错做,原码会变成0000 0000,反码编程0000 0000,结果为-2+3=0,到这里就不对起来了?
为什么会出现这样的情况呢?

就是因为二进制对于0的表达有两种方式,如下图表格所示
| 十进制数 | 原码 | 反码 |
| +0 | 0000 0000 | 0000 0000 |
| -0 | 1000 0000 | 1111 1111 |
| -1 | 1000 0001 | 1111 1110 |
| -2 | 1000 0010 | 1111 1101 |
怎么解决呢?这就引出了补码的由来
当初的哪些计算机大佬是那么想的:既然反码计算到0的时候会因为有2个0的表达方式而造成计算误差,那我把反码中的两个0的表达方式屏蔽一个不就好了嘛。所以就有了补码的出现

| 十进制数 | 原码 | 反码 | 补码 |
| +0 | 0000 0000 | 0000 0000 | 0000 0000 |
| -0 | 1000 0000 | 1111 1111 | 0000 0000 |
| -1 | 1000 0001 | 1111 1110 | 1111 1111 |
| -2 | 1000 0010 | 1111 1101 | 1111 1110 |
这样就可以把0的两种表现形式给屏蔽掉了,但是这里的补码是为了有负数、有反码的计算。
如果全部是正数的计算就用原码计算即可
补码
补码:为了解决反码不能计算负数超过0的问题而出现的
补码的示例
先把上面的表拿下来
| 十进制数 | 原码 | 反码 | 补码 |
| +0 | 0000 0000 | 0000 0000 | 0000 0000 |
| -0 | 1000 0000 | 1111 1111 | 0000 0000 |
| -1 | 1000 0001 | 1111 1110 | 1111 1111 |
| -2 | 1000 0010 | 1111 1101 | 1111 1110 |
| -3 | 1000 0011 | 1111 1100 | 1111 1101 |
| -4 | 1000 0100 | 1111 1011 | 1111 1100 |
举例一个跨0的情况,进行-4+5的操作
- -4的补码是1111 1100
- 5是一个正数。正数的原码、反码、补码的值都是一样的,所以补码为0000 0101
- 把两者补码进行相加操作,得到补码0000 0001,表示十进制的数就是1,成功!

这么一来,你就懂了吧?如果还没明白,把上面的步骤多看几遍,你就懂了
补码的小细节
因为补码是在反码的基础上+1得到的,所以-127的补码就是1000 0001,所以就会空出一位,因为+0和-0的补码是相同的,就会节省出一个补码跑到最下面,如下图所示
| 十进制数 | 原码 | 反码 | 补码 |
| +0 | 0000 0000 | 0000 0000 | 0000 0000 |
| -0 | 1000 0000 | 1111 1111 | 0000 0000 |
| -1 | 1000 0001 | 1111 1110 | 1111 1111 |
| -2 | 1000 0010 | 1111 1101 | 1111 1110 |
| -3 | 1000 0011 | 1111 1100 | 1111 1101 |
| -4 | 1000 0100 | 1111 1011 | 1111 1100 |
| ...... | ...... | ...... | ...... |
| -126 | 1111 1110 | 1000 0001 | 1000 0010 |
| -127 | 1111 1111 | 1000 0000 | 1000 0001 |
| -128 | 无 | 无 | 1000 0000 |
因为补码的这个特性,-128是特殊规定的,因此没有原码和反码。但是这也不影响,因为计算机中数字的存储和运算都是以补码为基础进行的
总结
原码是用来表示十进制数据的一种二进制形式,最左边的一位是符号位,0表示正数,1表示负数。但是,原码不能直接用于负数计算,如果用原码进行负数计算,结果会出错,实际运算的方向与正确运算的方向相反。
反码是为了解决原码不能计算负数的问题而出现的。对于正数,反码和原码一样;对于负数,反码是在原码的基础上将符号位不变,数值位全部取反(即0变1,1变0)。然而,反码也存在一个问题,那就是如果负数的计算结果跨过0,那么结果会比实际结果多1。
补码则是为了解决反码不能计算负数超过0的问题而出现的。对于正数,补码和原码、反码一样;对于负数,补码是在反码的基础上加1。这样,负数就可以正确地用补码表示了。此外,补码还可以多记录一个特殊的值-128,这在用一个字节表示数据的情况下是特别重要的。
