06 MIT线性代数-线性无关，基和维数Independence, basis, and dimension
1. 线性无关 Independence
Suppose A is m by n with m<n (more unknowns than equations)
Then there are nonzero solutions to Ax=0
Reason: there will be free variables! A中具有至少一个自由变量，那么Ax=0一定具有非零解。A的列向量可以线性组合得到零向量，所以A的列向量是线性相关的。
independence:vectors X1, X2,...,Xn are independent if no combination gives zero vectors (expect the zero comb. all Ci =0)
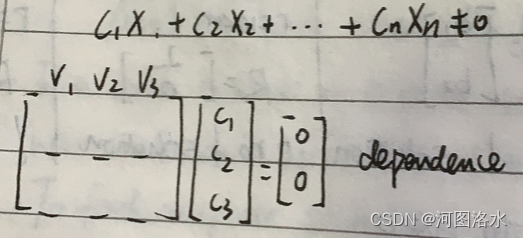
Repeat when v1,v2,..., vn are columns of A
they are independent if nullspace of A is zero vector , rank=n , N(A)={0}, no free variables 若这些向量作为列向量构成矩阵A，则方程Ax=0只有零解x=0，或称矩阵A的零空间只有零向量
they are dependent if Ac=0 for some nonzero C, rank<n , Yes free variables
结论:
此矩阵构成的方程Ax=0必有非零解，即三个向量线性相关
矩阵A的列向量为线性无关，则A所有的列均为主元列，没有自由列，矩阵的秩为n。
若A的列向量为线性相关，则矩阵的秩小于n，并且存在自由列
2. 张成空间 Spanning a space
vectors v1, v2, v3, ..., vn span a space means: The space consists of all combs. of those vectors
3. 基与维数Basis &Dimension
Basis for a space is a sequance of vectors v1, v2, ..., vd with 2 properties:
1. they are independent
2. they span the space
空间的基告诉我们了空间的一切信息
Example: Space is R3
standard: one basis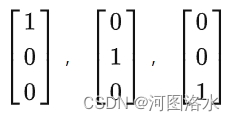 
Rn : n vectors give basis if the nxn matrix with those cols is invertible
3.1 子空间的基 Basis for a subspace
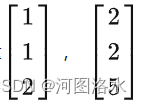可以张成R3中的一个平面，但是它们无法成为R3空间的一组基
Given a space: Every basis for the space has the same number of vectors (dimension of the space)
3.2 列空间和零空间的基 Basis of a column space and nullspace
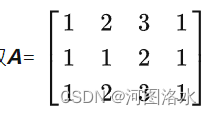
讨论列空间：
矩阵A的四个列向量张成了矩阵A的列空间，其中第3列和第4列与前两列线性相关，而前两个列向量线性无关。因此前两列为主元列。他们组成了列空间C(A)的一组基。矩阵的秩为2。
rank矩阵的秩r=# of pivot columns 矩阵主元列的数目=dimension of C(A)列空间的维数
讨论零空间：
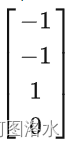必然在零空间N(A)之内
dim N(A)零空间的维数=自由列的数目# of free variables=n-r