【机器学习可解释性】2.特征重要性排列
机器学习可解释性
- 1.模型洞察的价值
- 2.特征重要性排列
- 3.部分依赖图
- 4.SHAP 值
- 5.SHAP值的高级使用
正文
前言
你的模型认为哪些特征最重要?
介绍
我们可能会对模型提出的最基本的问题之一是:哪些特征对预测的影响最大?
这个概念被称为特征重要性。
有多种方法可以衡量特征的重要性。一些方法巧妙地回答了上述问题的不同版本。其他方法也有不足之处。
在本课程中,我们将重点讨论排列的重要性。
与大多数其他方法相比,排列重要性是:快速计算,广泛使用和理解,并且与我们希望特征重要性度量具有的属性一致。
它的如何工作
排列重要性使用的模型与您目前看到的任何模型都不同,许多人一开始会感到困惑。所以我们将从一个例子开始,让它更具体。考虑以下格式的数据:

我们想利用10岁时的数据来预测一个人20岁时的身高。
我们的数据包括有用的特征(10岁时的身高)、几乎没有预测能力的特征(拥有袜子数),以及我们在解释中不会重点关注的其他一些特征。
在模型拟合后计算排列重要性。因此,我们不会改变模型,也不会改变对给定高度、袜子计数等值的预测结果。相反,我们将提出以下问题:如果我随机打乱验证数据的一列,而将目标列和所有其他列保留在原位,这将如何影响现在打乱的数据中预测的准确性?

随机重新排列一列应该会导致预测不太准确,因为得到的数据不再对应在现实世界中观察到的任何数据相对应。如果我们打乱模型在预测中严重依赖的列,模型的准确性尤其会受到影响。在这种情况下,Heigh at age 10(cm)会引起可怕的预测。如果Scoks owned at age 10数据打乱,那么由此产生的预测就不会受到太大的影响。
一个重要的列的数据打乱就会影响预测结果,如果不是重要的列打乱,对预测结果不会有太大的影响
有了这一认识,过程如下:
- 找一个受过训练的模型。
- 打乱单列中的值,使用生成的数据集进行预测。使用这些预测和真实的目标值来计算洗牌对损失函数的影响。这种性能恶化衡量的是你刚刚搅乱的变量的重要性。
- 将数据返回到原始顺序(取消步骤2中的打乱)。现在,对数据集中的下一列重复步骤2,直到计算出每一列的重要性。
代码示例
我们的示例将使用一个模型,该模型根据足球队的统计数据预测是否会有“本场最佳球员”。“最佳球员”奖是颁发给比赛中表现最好的球员的。模型构建不是我们当前的重点,因此下面的单元格将加载数据并构建一个基本模型。
预测2018年国际足联最佳球员 数据集为: FIFA 2018 Statistics数据集。字段包括日期、球队、对手、进球数、控球率、尝试次数、正中、偏离目标、封堵、角球、越位、任意球、扑救、传球准确率 %、传球、覆盖距离(公里)、犯规次数、黄牌、黄色和红色、红色、最佳球员、第一个进球、回合、PSO、PSO进球、乌龙球、乌龙球时间,共计27个字段组成。
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
data = pd.read_csv('../input/fifa-2018-match-statistics/FIFA 2018 Statistics.csv')
y = (data['Man of the Match'] == "Yes") # Convert from string "Yes"/"No" to binary
feature_names = [i for i in data.columns if data[i].dtype in [np.int64]]
X = data[feature_names]
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
my_model = RandomForestClassifier(n_estimators=100,
random_state=0).fit(train_X, train_y)
下面是如何使用eli5库计算和显示重要性:
import eli5
from eli5.sklearn import PermutationImportance
perm = PermutationImportance(my_model, random_state=1).fit(val_X, val_y)
eli5.show_weights(perm, feature_names = val_X.columns.tolist())
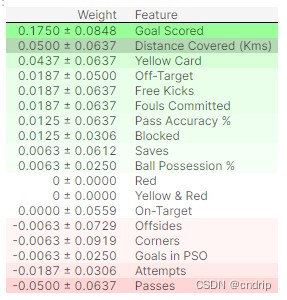
排列重要性的解读
表的顶部值是最重要的特征,表的底部的值最不重要。
每行中的第一个数字显示了随机打乱后模型性能下降的程度(在本例中,使用“准确性”作为性能指标)。
与数据科学中的大多数事情一样,对列进行打乱所导致的确切性能变化存在一定的随机性。我们通过多次打乱重复这一过程来衡量排列重要性计算中的随机性。± 后面的数字衡量了从一次打乱到下一次打乱的性能变化。
您偶尔会看到排列重要性会负值,在这些情况下,对混乱(或嘈杂)数据的预测碰巧比实际数据更准确。这种情况发生在特征无关紧要的时候(重要性应该接近于0),但是随机机会导致对打乱数据的预测更加准确。这在小型数据集(如本例中的数据集)中更常见,因为运气/机会的作用更大。
在我们的例子中,最重要的特征是进球。这似乎是明智的。对于其他变量的排序是否令人惊讶,球迷们可能有一些直觉。
轮到你了
从这里开始,灵活运用你新的排列重要性知识。
练习部分
简介
您将通过出租车票价预测比赛的数据样本来思考和计算排列重要性。
我们现在不会专注于数据探索或模型构建。你可以运行下面的单元格
- 加载数据
- 将数据划分为训练集和验证集
- 建立一个预测出租车票价的模型
- 打印几行供您查阅
纽约出租车价格预测 竞赛数据集 有5.3G,数据总量是5400W行,只有8个特征。
key:索引
fare_amount:价格
pickup_datetime:出租车接到客人的时间
pickup_longitude:出发时的经度
pickup_latitude:出发时的纬度
dropoff_longitude:到达时的经度
dropoff_latitude:到达时的纬度
passenger_count:乘客的数目
本文只导入前500W行的数据进行分析。加载数据、划分、数据处理以及用随机森林建模。
# 加载数据、划分、建模和EDA
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
data = pd.read_csv('../input/new-york-city-taxi-fare-prediction/train.csv', nrows=50000)
# 删除具有极端异常坐标或负票价的数据
data = data.query('pickup_latitude > 40.7 and pickup_latitude < 40.8 and ' +
'dropoff_latitude > 40.7 and dropoff_latitude < 40.8 and ' +
'pickup_longitude > -74 and pickup_longitude < -73.9 and ' +
'dropoff_longitude > -74 and dropoff_longitude < -73.9 and ' +
'fare_amount > 0'
)
y = data.fare_amount
base_features = ['pickup_longitude',
'pickup_latitude',
'dropoff_longitude',
'dropoff_latitude',
'passenger_count']
X = data[base_features]
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
first_model = RandomForestRegressor(n_estimators=50, random_state=1).fit(train_X, train_y)
# 反馈系统的环境设置
from learntools.core import binder
binder.bind(globals())
from learntools.ml_explainability.ex2 import *
print("Setup Complete")
# 显示数据
print("Data sample:")
data.head()
Data sample:
| key | fare_amount | pickup_datetime | pickup_longitude | pickup_latitude | dropoff_longitude | dropoff_latitude | passenger_count |
|---|---|---|---|---|---|---|---|
| 2 | 2011-08-18 00:35:00.00000049 | 5.7 | 2011-08-18 00:35:00 UTC | -73.982738 | 40.761270 | -73.991242 | 40.750562 |
| 3 | 2012-04-21 04:30:42.0000001 | 7.7 | 2012-04-21 04:30:42 UTC | -73.987130 | 40.733143 | -73.991567 | 40.758092 |
| 4 | 2010-03-09 07:51:00.000000135 | 5.3 | 2010-03-09 07:51:00 UTC | -73.968095 | 40.768008 | -73.956655 | 40.783762 |
| 6 | 2012-11-20 20:35:00.0000001 | 7.5 | 2012-11-20 20:35:00 UTC | -73.980002 | 40.751662 | -73.973802 | 40.764842 |
| 7 | 2012-01-04 17:22:00.00000081 | 16.5 | 2012-01-04 17:22:00 UTC | -73.951300 | 40.774138 | -73.990095 | 40.751048 |
以下两个单元格也可能有助于理解训练数据中的值:
train_X.describe()
| – | pickup_longitude | pickup_latitude | dropoff_longitude | dropoff_latitude | passenger_count |
|---|---|---|---|---|---|
| count | 23466.000000 | 23466.000000 | 23466.000000 | 23466.000000 | 23466.000000 |
| mean | -73.976827 | 40.756931 | -73.975359 | 40.757434 | 1.662320 |
| std | 0.014625 | 0.018206 | 0.015930 | 0.018659 | 1.290729 |
| min | -73.999999 | 40.700013 | -73.999999 | 40.700020 | 0.000000 |
| 25% | -73.987964 | 40.744901 | -73.987143 | 40.745756 | 1.000000 |
| 50% | -73.979629 | 40.758076 | -73.978588 | 40.758542 | 1.000000 |
| 75% | -73.967797 | 40.769602 | -73.966459 | 40.770406 | 2.000000 |
| max | -73.900062 | 40.799952 | -73.900062 | 40.799999 | 6.000000 |
train_y.describe()
count 23466.000000
mean 8.472539
std 4.609747
min 0.010000
25% 5.500000
50% 7.500000
75% 10.100000
max 165.000000
Name: fare_amount, dtype: float64
问题 1
第一个模型使用以下特征
- pickup_longitude:出发时的经度
- pickup_latitude:出发时的纬度
- dropoff_longitude:到达时的经度
- dropoff_latitude:到达时的纬度
- passenger_count:乘客的数目
在运行任何代码之前。。。哪些变量似乎对预测出租车票价有用?你认为排列重要性必然会将这些特征识别为重要特征吗?
一旦你考虑过了,在运行代码之前,运行下面的q_1.solution()看看你会怎么想。
# 检查你的答案 (Run this code cell to receive credit!)
q_1.solution()
结论:了解纽约市出租车的价格是否会根据乘客数量而有所不同会很有帮助。大多数地方不会根据乘客人数改变票价。如果你认为纽约市是一样的,那么只有列出的前4个特征才是重要的。乍一看,所有这些似乎都同等重要。
问题 2
创建一个名为perm的PermutationImportance对象,以显示first_model中的重要性。使用适当的数据进行拟合,并显示权重。
为了方便起见,教程中的代码已复制到此代码单元中的注释中。
import eli5
from eli5.sklearn import PermutationImportance
# 对下面的代码进行一个小的更改以用于此问题。
# perm = PermutationImportance(my_model, random_state=1).fit(val_X, val_y)
# 检查你的答案
q_2.check()
# 注释以下行以可视化结果
# eli5.show_weights(perm, feature_names = val_X.columns.tolist())
答案:
将一行修改为
# perm = PermutationImportance(my_model, random_state=1).fit(val_X, val_y)
把前面的# 注释掉
perm = PermutationImportance(first, random_state=1).fit(val_X, val_y)
干得好!:请注意,每次运行的分数可能略有不同。但总体情况的发现每次都会保持不变。
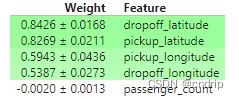
问题 3
在看到这些结果之前,我们可能已经预料到4个方向特征中的每一个都同样重要。
但是就一般而言,纬度特征比经度特征更重要。你能对此提出任何假设吗?
仔细考虑后,请查看此处以了解一些可能的解释:
结论:
1.旅行的纬度距离可能比经度距离大。如果经度值通常更接近,那么调整它们就没那么重要了。
2.城市的不同地区可能有不同的定价规则(例如每英里的价格),定价规则可能因纬度而非经度而异。
3.向北<->向南(纬度变化)的道路的收费可能高于向东<->向西(经度变化)的公路。因此,纬度将对预测产生更大的影响,因为它捕捉到了通行费的金额。
问题 4
如果没有对纽约市的详细了解,很难排除大多数关于纬度特征比经度更重要的假设。
一个好的下一步是将身处城市某些地区的影响与旅行总距离的影响区分开来。
下面的代码为纵向和横向距离创建了新特征。然后,它构建了一个模型,将这些新特征添加到您已经拥有的特征中。
填写两行代码来计算并显示具有这组新特征的重要性权重。和前面一样,您可以取消对以下行的注释,以检查代码、查看提示或获取答案。
# create new features
data['abs_lon_change'] = abs(data.dropoff_longitude - data.pickup_longitude)
data['abs_lat_change'] = abs(data.dropoff_latitude - data.pickup_latitude)
features_2 = ['pickup_longitude',
'pickup_latitude',
'dropoff_longitude',
'dropoff_latitude',
'abs_lat_change',
'abs_lon_change']
X = data[features_2]
new_train_X, new_val_X, new_train_y, new_val_y = train_test_split(X, y, random_state=1)
second_model = RandomForestRegressor(n_estimators=30, random_state=1).fit(new_train_X, new_train_y)
# 在second_model上创建一个PermutationImportance对象,并将其调整为new_val_X和new_valy_y
# 对于与预期解决方案匹配的可重复结果,请使用random_state=1
perm2 = ____
# 显示您刚刚计算的排列重要性的权重
____
# 检查你的答案
q_4.check()
答案:
perm2 = PermutationImportance(second_model, random_state=1).fit(new_val_X, new_val_y)
eli5.show_weights(perm2, feature_names = features_2 )
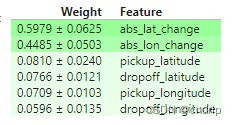
你会如何解读这些重要性分数?旅行距离似乎比任何位置效应都重要得多。
但位置仍然会影响模型预测,下客位置现在比接送位置更重要。你对为什么会这样有任何假设吗?下一课中的技巧将帮助你深入了解这一点。
# Check your answer (Run this code cell to receive credit!)
q_4.solution()
问题 5
一位同事观察到,abs_lon_change 和 abs_lat_change 的值非常小(所有值都在-0.1到0.1之间),而其他变量的值更大。你认为这可以解释为什么这些坐标在这种情况下具有更大的排列重要性值吗?
考虑一个替代方案,您创建并使用了一个特征,该特征的大小是这些特征的100倍,并将该更大的特征用于训练和重要性计算。这会改变输出的置换重要性值吗?
为什么呢?
在你思考了你的答案后,可以尝试这个实验,也可以在下面的单元格中查找答案。
答案
将这个
data['abs_lon_change']和data['abs_lat_change']扩大100倍。查看结果。
# create new features
data['abs_lon_change'] = abs(data.dropoff_longitude - data.pickup_longitude)*100
data['abs_lat_change'] = abs(data.dropoff_latitude - data.pickup_latitude)*100
features_2 = ['pickup_longitude',
'pickup_latitude',
'dropoff_longitude',
'dropoff_latitude',
'abs_lat_change',
'abs_lon_change']
X = data[features_2]
new_train_X, new_val_X, new_train_y, new_val_y = train_test_split(X, y, random_state=1)
second_model = RandomForestRegressor(n_estimators=30, random_state=1).fit(new_train_X, new_train_y)
# Create a PermutationImportance object on second_model and fit it to new_val_X and new_val_y
# Use a random_state of 1 for reproducible results that match the expected solution.
perm2 = PermutationImportance(second_model, random_state=1).fit(new_val_X, new_val_y)
# show the weights for the permutation importance you just calculated
eli5.show_weights(perm2, feature_names =features_2)
# Check your answer
q_4.check()
# Check your answer (Run this code cell to receive credit!)
q_5.solution()
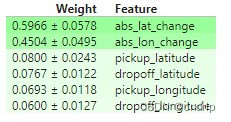
结论:特征的规模本身并不影响排列的重要性。重新缩放特征会间接影响PI的唯一原因是,如果重新缩放有助于或损害我们使用的特定学习方法利用该特征的能力。这种情况不会发生在基于树的模型中,比如这里使用的随机森林。如果你熟悉Ridge回归,你可能会想到它是如何受到影响的。也就是说,绝对变化特征非常重要,因为它们捕获了行驶的总距离,这是出租车费用的主要决定因素……它不是特征幅度的一个人工产物。
问题 6
您已经看到,横向距离的特征重要性大于纵向距离的重要性。由此,我们能否得出结论,在固定的横向距离上旅行是否比在相同的纵向距离上旅行更昂贵?
为什么?请检查下面的答案。
# Check your answer (Run this code cell to receive credit!)
q_6.solution()
结论::我们不能从排列重要性结果中判断出沿固定的纬度距离旅行比沿相同的纵向距离旅行更昂贵还是更便宜。纬度特征比经度特征更重要的可能原因
1.数据集中的纬度距离趋于较大
2.沿纬度走固定的距离会比较贵。
如果abs_lon_change值非常小,经度对模型的重要性就会降低,即使在该方向上每英里的旅行成本很高。
继续深入
排列重要性对于调试、理解模型以及传达模型的高级概述非常有用。
接下来,了解部分偏依赖图,了解每个特征如何影响预测。
