【C++】搜索二叉树(保姆教程)
🍅二叉树底层是堆,之前学习的简单二叉树不是大堆就是小堆,今天是二叉树进阶,一定要好好掌握!
目录
☃️1.搜索二叉树介绍
☃️2.底层实现
☃️3.key模型和key,value模型
☃️1.搜索二叉树介绍
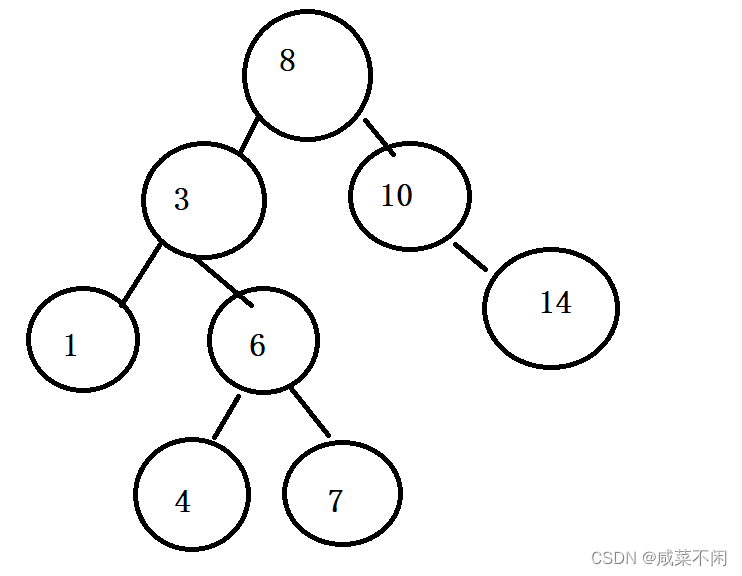
右>根>左 这样结构的树就是搜索二叉树,显然,他的主要功能:搜索,因为想要找到x,首先和根比较,如果比根大,那么走右子树(右子树所有节点值都比root大),否则走左子树(左子树所有节点值比root小)
次要功能:排序
☃️2.底层实现
首先我们定义一个命名域,然后把下面写的所有代码封装进去
先定义一个树的节点,他是一个class也行(只不过应该写成public)那还不如写成struct,然后要保存做左孩子和右孩子,还要保存自己的节点值,并且附上初始化,方便后面用val去new,初始化的时候直接初始化列表即可,注意初始化列表的格式

然后就是整个树的类
首先把类型重命名一下,每个树的节点类型应该是node<class K>*
重命名的时候带不带*都行,我这里没带,后面每个节点需要写成Node*
带上*,后面每个节点写成Node即可

类里面的成员变量只有根节点
首先写一个构造函数

然后插入(非递归)
搜索树不允许插入重复的节点,所以要写成bool类型,不可以是void
我们先捋一下思路
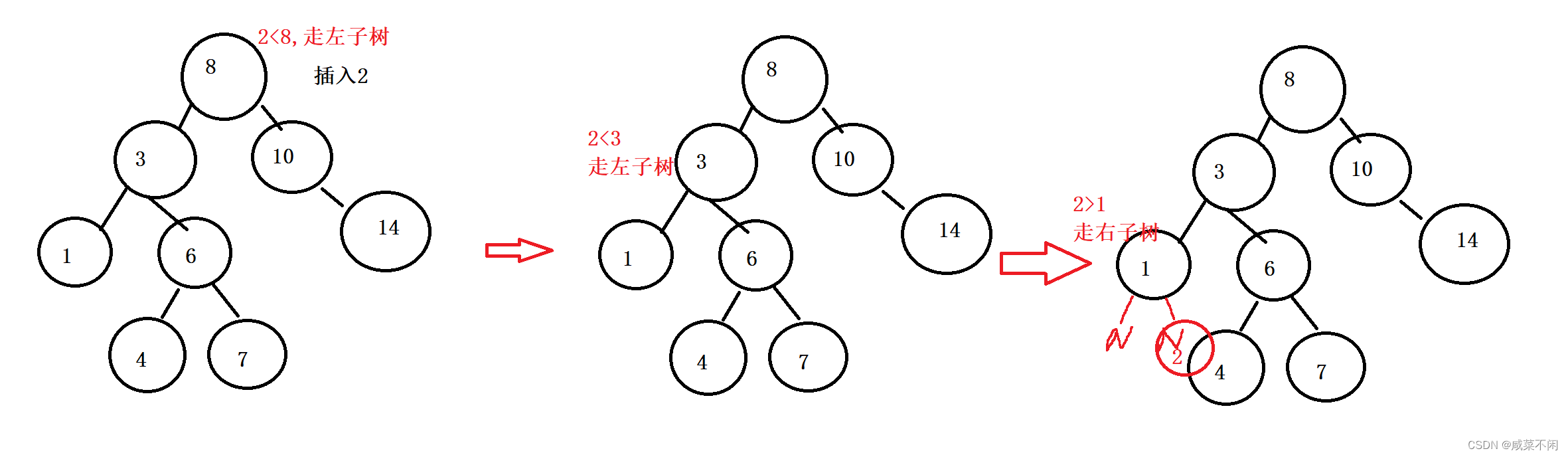
发现这个就是来回比较的过程,如果找到了要插入的位置,还需要知道他的父节点(为了链接)
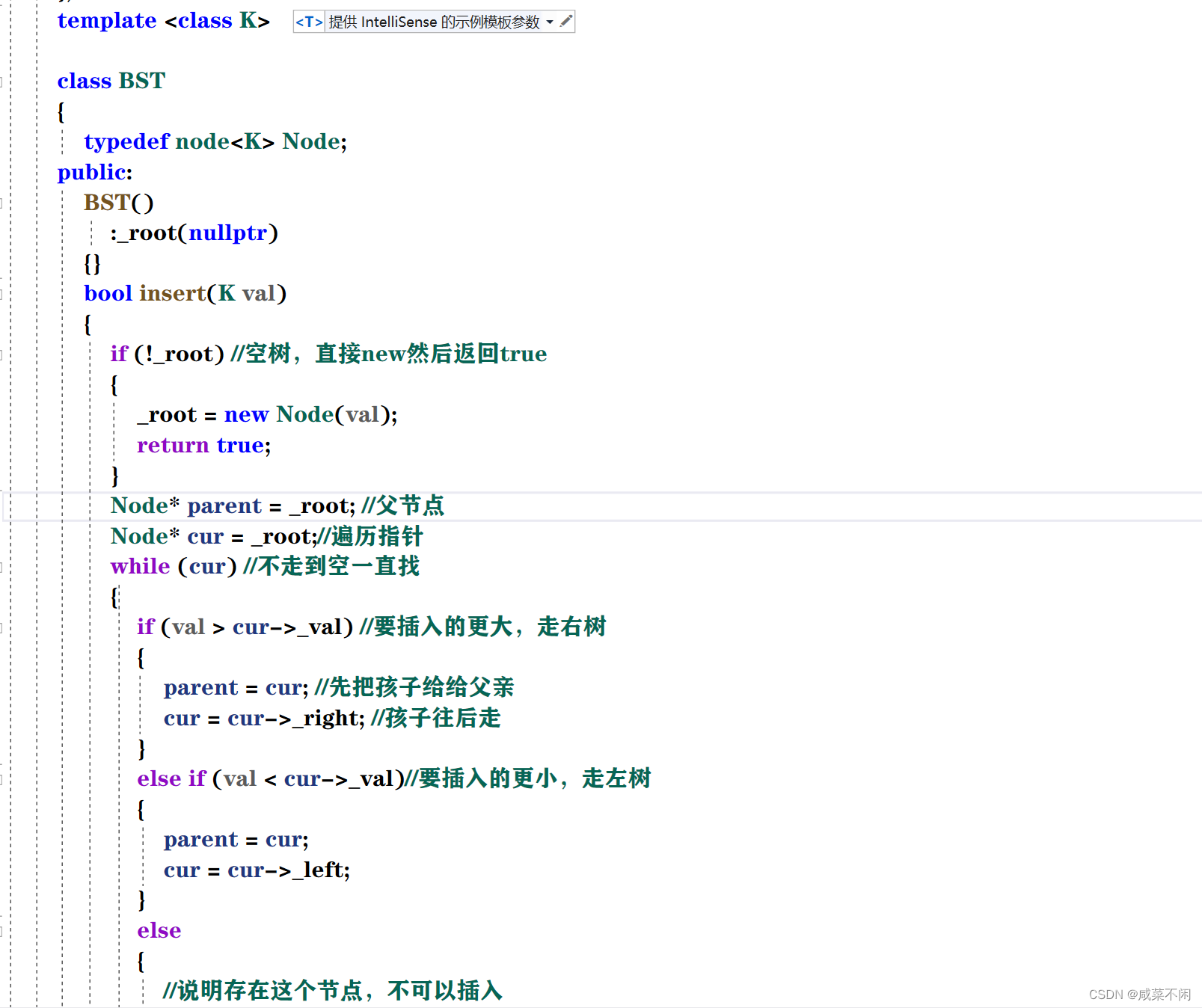
template <class K>
class BST
{
typedef node<K> Node;
public:
BST()
:_root(nullptr)
{}
bool insert(K val)
{
if (!_root) //空树,直接new然后返回true
{
_root = new Node(val);
return true;
}
Node* parent = _root; //父节点
Node* cur = _root;//遍历指针
while (cur) //不走到空一直找
{
if (val > cur->_val) //要插入的更大,走右树
{
parent = cur; //先把孩子给给父亲
cur = cur->_right; //孩子往后走
}
else if (val < cur->_val)//要插入的更小,走左树
{
parent = cur;
cur = cur->_left;
}
else
{
//说明存在这个节点,不可以插入
return false;
}
}
Node* newnode = new Node(val); //找到要插入的位置,new
if (parent->_val > val) //判断往父节点的左/右插,节点val更大,说明要插入的更小,应该在左孩子
{
parent->_left = newnode;
}
else
{
parent->_right = newnode; //否则在右孩子
}
return true; //插入成功
}还要查找节点函数
具体的搜索思想和刚才是一样的

bool find(const K& val)
{
if (!_root) return false; //空树肯定找不到
Node* cur = _root; //遍历指针
while (cur)
{
if (cur->_val == val) return true; //找到啦
else if (val < cur->_val) //搜索思想,不再赘述
{
cur = cur->_left;
}
else
{
cur = cur->_right;
}
}
return false;
}
中序遍历,打印二叉树
注意:这时候需要用到节点,但是根节点是私有的,我们可以写一个getroot的函数,但是最好不要破坏封装性,在函数里调用一个私有成员函数

void InOrder()
{
if (!_root) return;
_InOrder(_root);//调用私有成员函数
cout << endl; //打印之后换行
}私有成员函数:

void _InOrder(Node* root)
{
if (!root) return; //截断条件
_InOrder(root->_left); //左
cout << root->_val << " ";//根
_InOrder(root->_right);//右
}删除值为val的节点,如果没有返回false
要删除一个节点,要把他的父节点和其他节点连接上,所以也要保留父亲
先看搜索节点的部分

判断一下是不是因为没找到目标节点才退出的

正常删除
首先要删节点左为空的情况
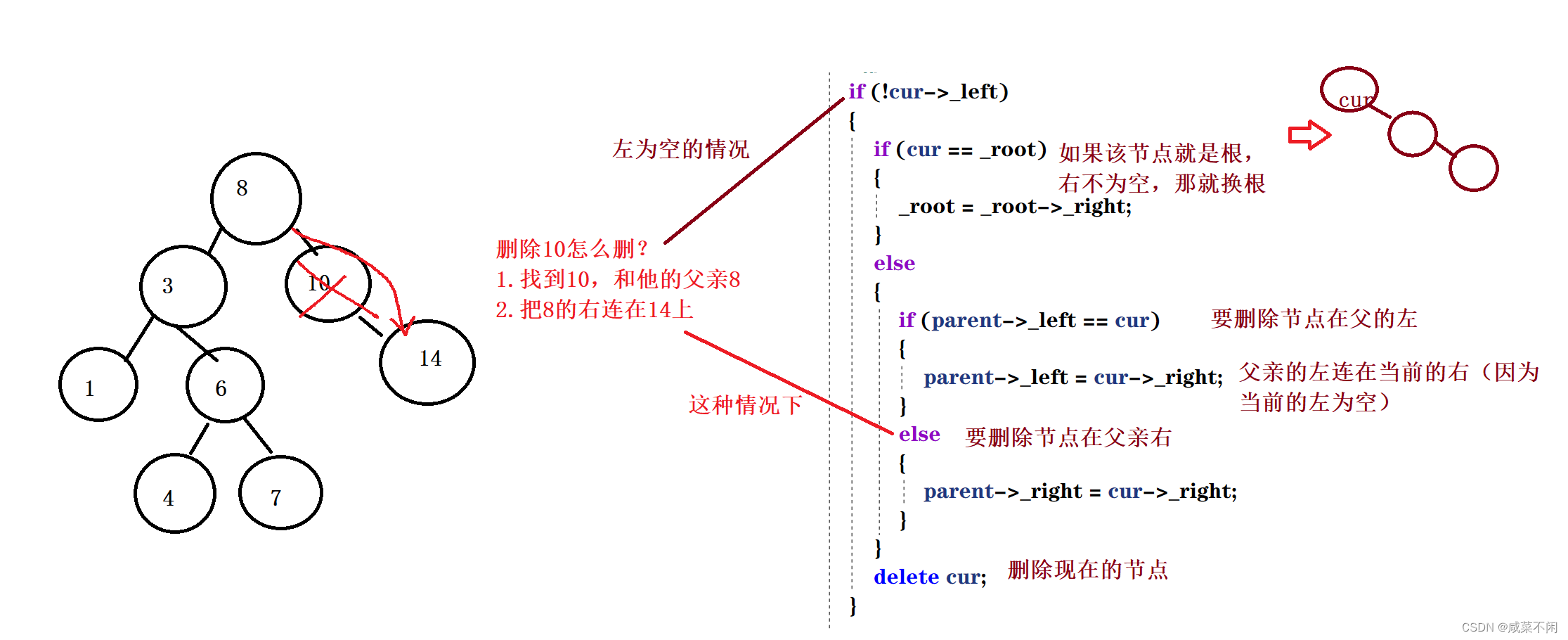
要删节点右为空,完全类似作为空,不赘述

左右都不为空(删的不是叶子节点)

思考:要是删的是root,不能写成,否则就是空指针的解引用


最后完整的删除代码
bool Erase(const K& val)
{
if (!_root) return false; //空树不删除
Node* cur = _root; //遍历指针
Node* parent = _root; //父节点
while (cur)
{
//首先找到要删除的节点,找不到直接false
if (val > cur->_val) //搜索逻辑
{
parent = cur;
cur = cur->_right;
}
else if (val < cur->_val)
{
parent = cur;
cur = cur->_left;
}
else
{
break;
}
}
if (!cur)
return false;//如果循环条件结束是因为每找到节点,直接false
//左为空
//右为空
//都不为空
if (!cur->_left)
{
if (cur == _root)
{
_root = _root->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (!cur->_right)
{
if (cur == _root)
{
_root = _root->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
}
else
{
Node* parent = cur; //保存父节点
Node* minRight = cur->_right; //找右树最小
while (minRight->_left) //找小往左树走
{
//此时的父节点是要删除minRight的父节点
parent = minRight;
minRight = minRight->_left;
}
cur->_val = minRight->_val; //找到右树最小,把他和要删除节点值交换
if (minRight == parent->_left) //如果最小在父亲的左侧
{
parent->_left = minRight->_right;
//父亲左连minRight右,因为minRight的左一定是NULL(他是最小的)如果右节点还有一定要连上
}
else
{
parent->_right = minRight->_right;//父亲右连minRight右
}
delete minRight;
}
return true;
}左右都不为空时找左树最大也可以
else
{
Node* parent = cur; //保存父节点
Node* maxleft = cur->_left;
while (maxleft->_right)
{
parent = maxleft;
maxleft = maxleft->_right;
}
cur->_val = maxleft->_val;
if (maxleft == parent->_left)
parent->_left = maxleft->_left;
else
parent->_right = maxleft->_left;
delete maxleft;
}Find的递归版本,递归需要传根,所以还是写成调用私有吧成员函数的形式


bool _FindR(Node* root, const K& val)
{
if (!root) return false;
if (root->_val > val)
{
//左
_FindR(root->_left, val);
}
else if (root->_val < val)
{
_FindR(root->_right, val);
}
else
{
return true;
}
}插入的递归版本

看一个错误写法

问题在图片中写出了,无法连接
那么怎么做?给节点加上引用

比如要插入2
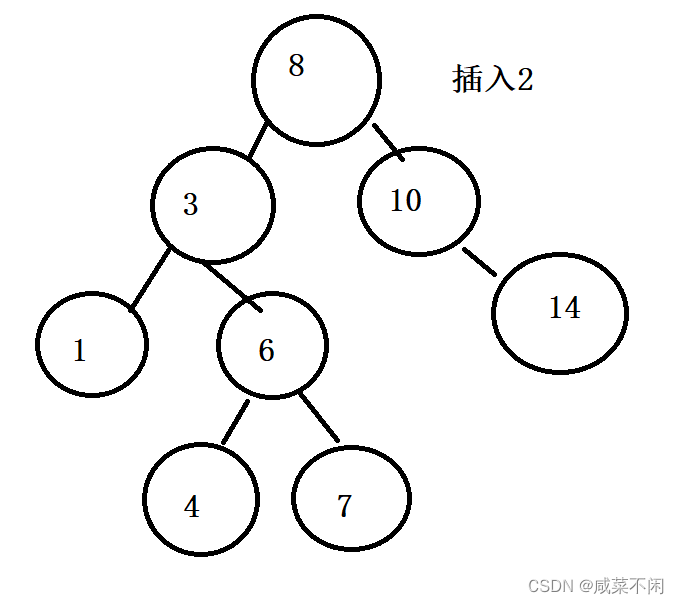
可以递归找到插入位置在1的右
此时root是nullptr,但也是1右孩子的别名,给root开空间,就是给1右孩子开空间
bool _InsertR(Node*& root, const K& val)
{
if (!root) //root是他父节点的某个孩子的别名
{
root = new Node(val);//把孩子new,自然和父亲有链接
return true;
}
if (root->_val > val)
_InsertR(root->_left, val);
else if (root->_val < val)
_InsertR(root->_right, val);
else
return false;
}删除递归

整体思路和刚才一样的吗,只不过都不为空稍有变化
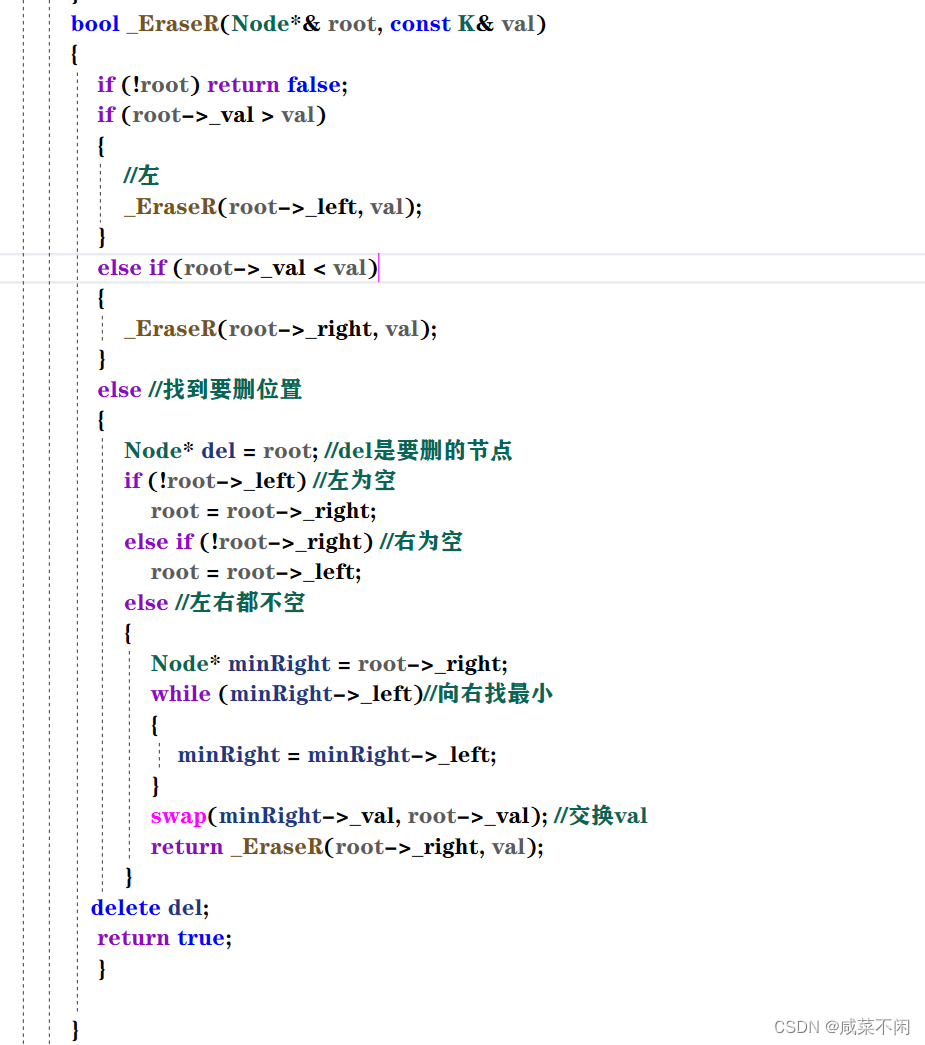
 同样的找左树最大当替死鬼也可以
同样的找左树最大当替死鬼也可以
写一个copy函数(需要根,写成调用私有成员函数)


Node* _Copy(Node* root)
{
if (!root) return nullptr;
Node* newnode = new Node(root->_val);
newnode->_left = _Copy(root->_left);
newnode->_right = _Copy(root->_right);
return newnode;
}还有不销毁函数
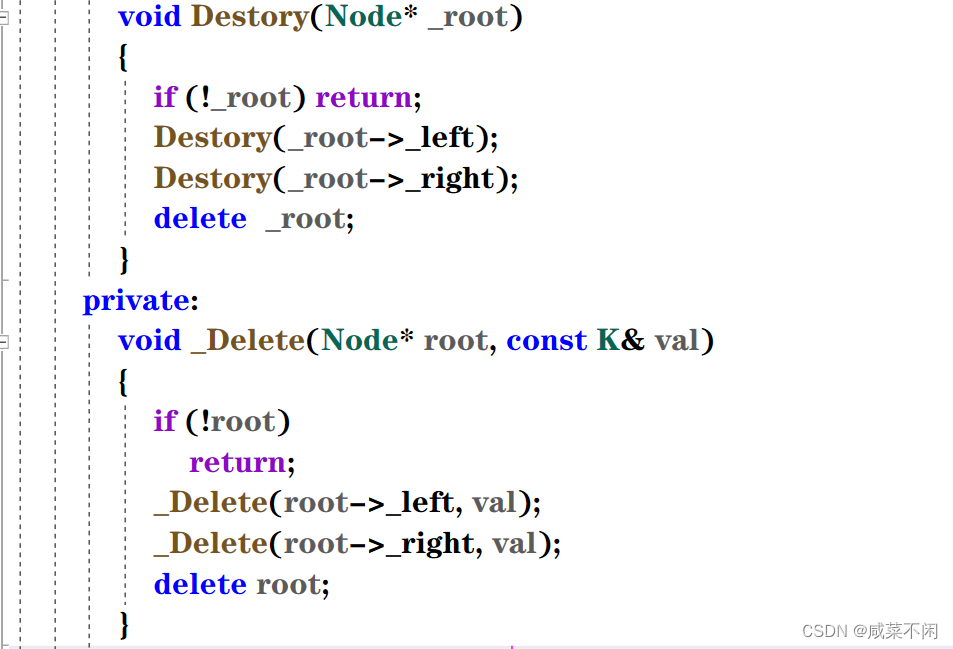
void _Delete(Node* root, const K& val)
{
if (!root)
return;
_Delete(root->_left, val);
_Delete(root->_right, val);
delete root;
}基本上最难最重要的就是删除函数,我们已经实现的差不多啦
最后补全析构函数和构造函数

BST()
:_root(nullptr)
{}
BST(const BST<K>& t)
{
_root = Copy(t._root);
}
BST<K>& operator=(BST<K> t)
{
swap(_root, t._root);
return *this;
}
☃️3.key模型和key,value模型
key模型就是刚才讲的搜索树,每个节点的val就是模型里的key,
key value模型是用一个值找另一个信息的过程
比如用手机号查快递,用学号查分数
具体的代码和刚才没有很大区别,只是多了一个模板参数,和节点的变量值
namespace KV
{
template<class K,class V>
struct BTNode
{
BTNode<K, V>* _left;
BTNode<K, V>* _right;
V _val;
K _key;
BTNode(const K& key, const V& val)
:_key(key)
,_val(val)
,_right(nullptr)
,_left(nullptr)
{}
};
template<class K, class V>
class Tree
{
typedef BTNode<K, V> Node;
public:
bool Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
void Inorder()
{
_Inorder(_root);
}
void _Inorder(Node* root)
{
if (root == nullptr)
return;
_Inorder(root->_left);
cout << root->_key << ":" << root->_val << endl;
_Inorder(root->_right);
}
private:
Node* _root = nullptr;
};比如他可以帮我统计一个字符串数组中每个字符串出现的个数
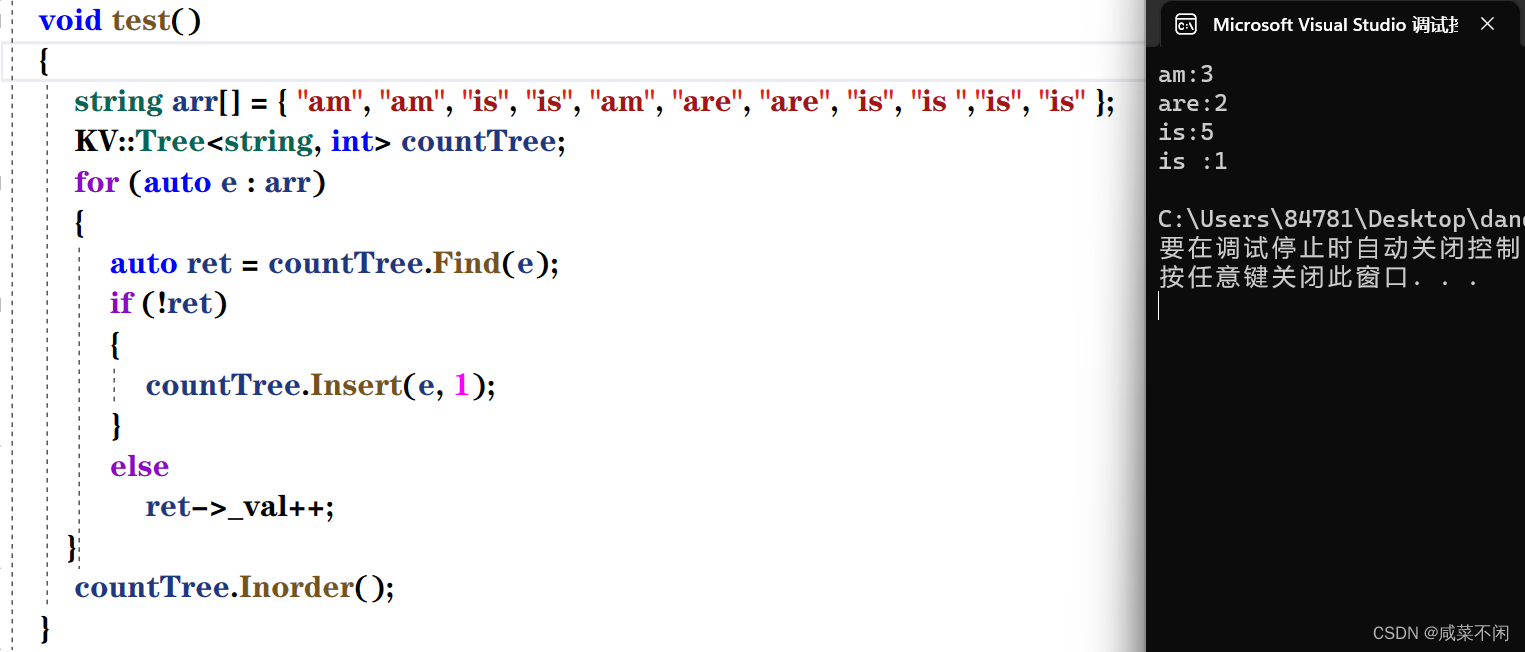
k模型和kv模型是解决问题的两种不同手段
