当前位置：首页 > article >正文

【机器视觉------标定篇（二）】三点成圆算法（求相机旋转中心）

article 2024/9/20 0:03:20

应用场景

机器视觉项目应用中，相机安装在机器人上，并且需要定位产品返回坐标偏差以及角度偏差。
与九点标定配合使用，实现精准角度补偿。

算法输入

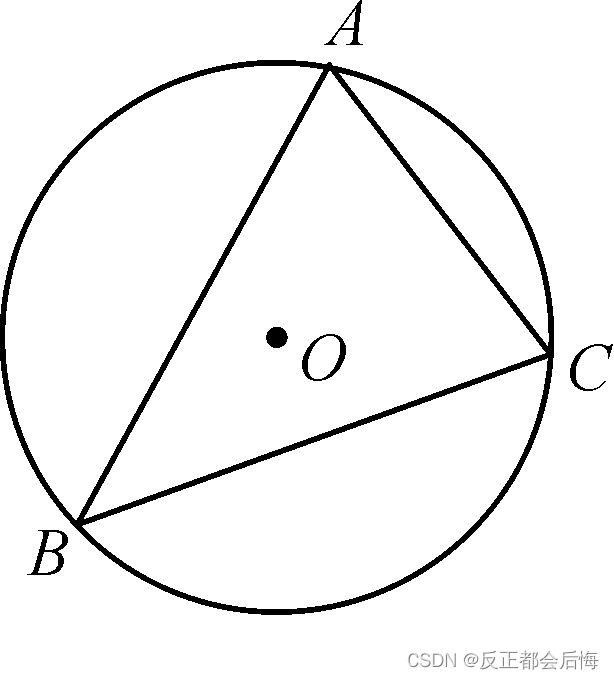
不共线的三点坐标 A（X₁,Y₁），B（X₂,Y₂） ,C（X₃,Y₃）
在这里插入图片描述

算法原理及实现

原理：

由图可知，线OA=OB=OC=外接圆的半径（r）,从三点向【以O点为原点的坐标系】做垂线。由勾股定理可得：

（X - X₀）² + （Y - Y₀）² = r ²

由上式带入三点坐标可的可得：
在这里插入图片描述
公式变换可得（由公式①-②，①-③）：
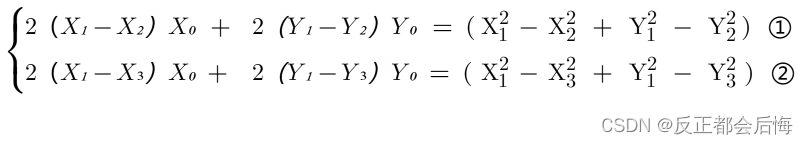
计算圆心公式
由于上公式可得，该式有唯一解的条件为：

即任两点组成的斜率不能相等，也验证了三点成圆条件：三点不共线。

实现：

设：
a = 2(X₁ - X₂)
b = 2(Y₁ - Y₂)

c = 2(X₁ - X₃)
d= 2(Y₁ - Y₃)

e = (X₁)² - (X₂)² + (Y₁)² - (Y₂)²
f = (X₁)² - (X₃)² + (Y₃)² - (Y₃)²

代回方程:
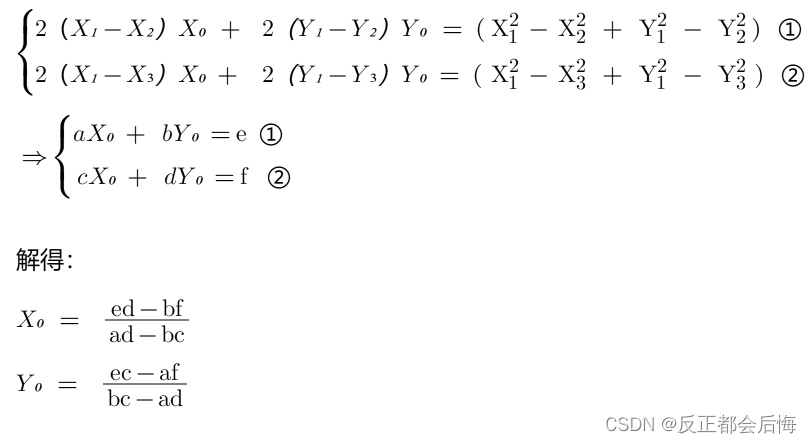
在这里插入图片描述

代码实现

 public PointF CalculateCicular(PointF px1, PointF px2, PointF px3)
{
	float x1, y1, x2, y2, x3, y3;
	float a, b, c, g, e, f, X, Y;
	x1 = px1.X;
	y1 = px1.Y;
    x2 = px2.X;
    y2 = px2.Y;
    x3 = px3.X;
    y3 = px3.Y;
    a = 2 * (x1 - x2);
    b = 2 * (y1 - y2);

    c = 2 * (x1 - x3);
    d = 2 * (y1 - y3);
    
    e = x1 * x1 - x2 * x2 + y1 * y1 - y2 * y2;
    f = x1 * x1 - x3 * x3 + y1 * y1 - y3 * y3;
    
    X = (e * d - b * f) / (a * d - b * c);  
    Y = (e * c - a * f) / (b * c - a * d);
    //R = (float)Math.Sqrt((X - x1) * (X - x1) + (Y - y1) * (Y - y1)); //半径

     PointF center = new PointF(X, Y);
     return center;
}