Leetcode刷题详解——不同路径
1. 题目链接:62. 不同路径
2. 题目描述:
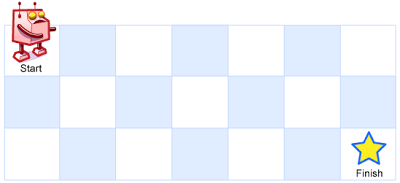
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3 输出:28示例 4:
输入:m = 3, n = 3 输出:6提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
解法1(暴力搜索):
【由于复杂度太高会超时】
算法思路:
-
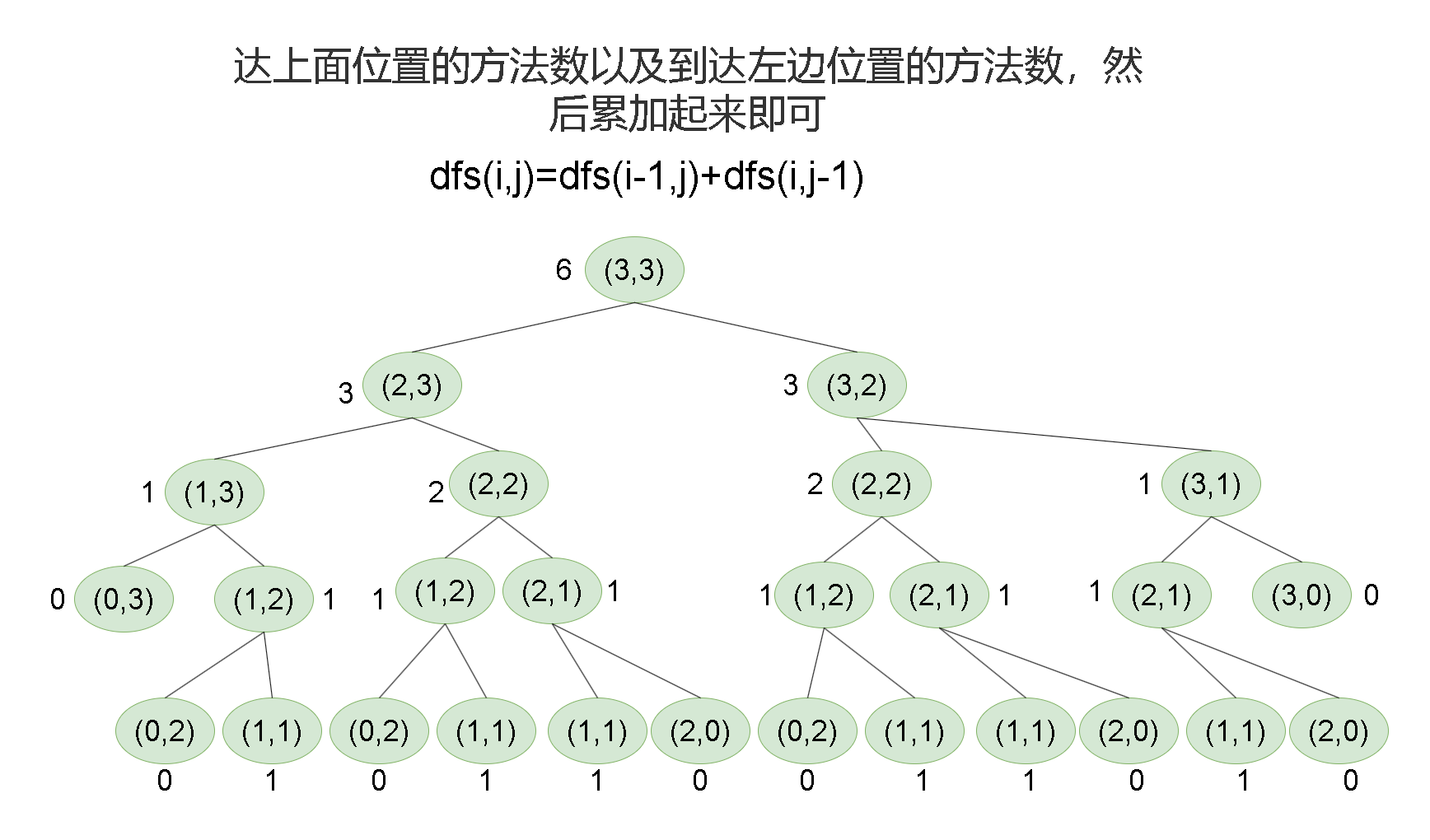
递归含义:给
dfs一个使命,给他一个下标,返回从[0,0]位置走到[i,j]位置一共有多少种方法 -
函数体:只要知道到达上面位置的方法数以及到达左边位置的方法数,然后累加起来即可
-
递归出口:当下标越界的时候返回0;当前位于起点的时候,返回1
C++算法代码:
class Solution {
public:
int uniquePaths(int m, int n) {
return dfs(m,n);
}
int dfs(int i,int j)
{
if(i==0||j==0) return 0;
if(i==1&&j==1) return 1;
return dfs(i-1,j)+dfs(i,j-1);
}
};
解法2(记忆化搜索):
算法思路:
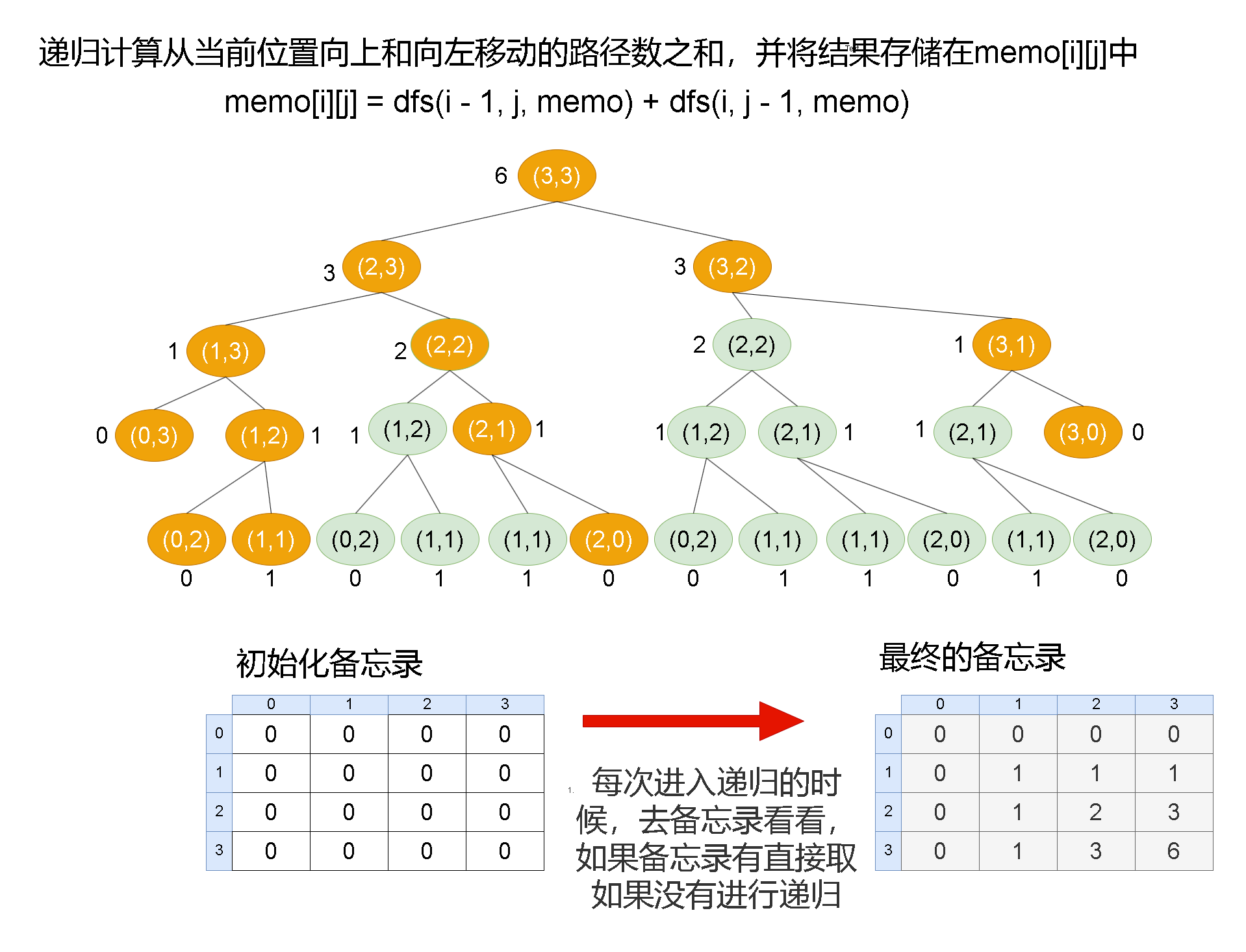
- 加上一个备忘录
- 每次进入递归的时候,去备忘录看看
- 每次返回的时候,将结果加入到备忘录里面
C++算法代码:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> memo(m+1, vector<int>(n+1)); // 创建一个二维数组memo,用于存储已经计算过的路径数
return dfs(m, n, memo); // 调用深度优先搜索函数dfs,传入参数m、n和memo
}
int dfs(int i, int j, vector<vector<int>>& memo) {
if (memo[i][j] != 0) { // 如果memo[i][j]不为0,说明已经计算过这个位置的路径数,直接返回memo[i][j]
return memo[i][j];
}
if (i == 0 || j == 0) return 0; // 如果i或j为0,说明已经到达边界,无法继续前进,返回0
if (i == 1 && j == 1) { // 如果i和j都为1,说明已经到达终点,返回1
memo[i][j] = 1;
return 1;
}
memo[i][j] = dfs(i - 1, j, memo) + dfs(i, j - 1, memo); // 递归计算从当前位置向上和向左移动的路径数之和,并将结果存储在memo[i][j]中
return memo[i][j]; // 返回memo[i][j]作为结果
}
};
解法3(动态规划):
算法思路:
- 函数含义->状态表示
- 函数体->状态转移方程
- 递归出口->初始化
C++算法代码:
class Solution {
public:
int uniquePaths(int m, int n) {
// 创建一个二维数组dp,大小为(m+1) x (n+1),用于存储每个位置的路径数
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 初始化起点的路径数为1
dp[1][1] = 1;
// 遍历二维数组,计算每个位置的路径数
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 如果当前位置是起点,跳过
if (i == 1 && j == 1) continue;
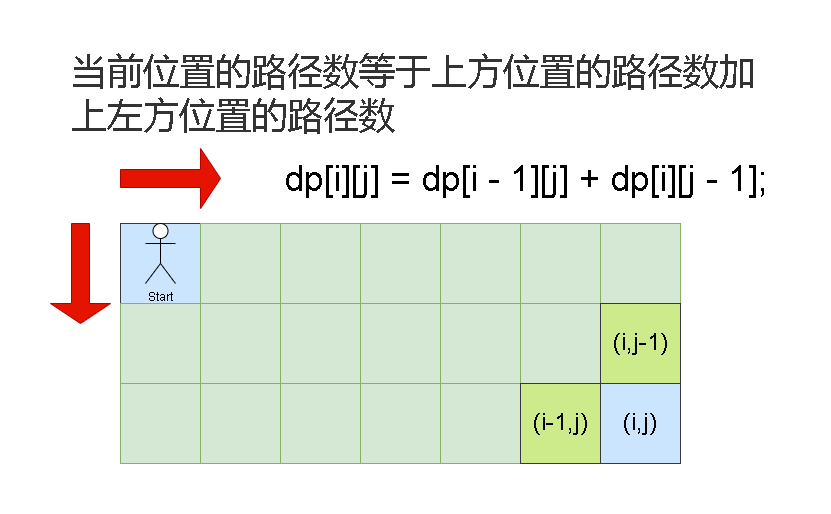
// 当前位置的路径数等于上方位置的路径数加上左方位置的路径数
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
// 返回终点的路径数
return dp[m][n];
}
};