[深度学习]卷积神经网络的概念,入门构建(代码实例)
# 不再任何人,任何组织的身上倾注任何的感情,或许这就是能活得更开心的办法
0.写在前面:
卷积神经网络的部分在之前就已经有所接触,这里重新更全面地总结一下关于深度学习中卷积神经网络的部分.并且在这里对如何构建代码,一些新的思想和网络做出一点点补充,同时会持续更新一些注入残差网络等现代的卷积网络部分.
简言之,入门看这篇就行.........
1.关于卷积网络的概念:
在一些图片处理之类的问题中,我们不可避免地会碰到一些环境监测的工作,其实正常来说,神经网络读取的数据肯定是矩阵,张量,为了保证图像的严整性,我们需要把每个像素都抽象化为一个具体的数字,这就会带来两个问题:
1.对于图像数据来说,需要考虑的是一个上下文的环境,换句话说,例如对人物,车辆的识别工作,不可能对像素进行处理.
2.另一个角度来说,我们在之前的多层感知机中使用了展平层来处理三维数据,这样子处理以后不仅不符合逻辑,计算量也很大,因此要引入卷积神经网络的概念.
并且不只是图像,对于一些大预言模型的处理,我们需要对传输数据进行一定的画框,然后分批次进行读取. 另外就是我最近在座的生物信息分析的数据,更需要考虑到其中一个上下文的环境
例如有一段生物信息代码:
ACTUTCCTAA例如这段生物信息为例,我们在做数据分析的时候不能盲目地转化为[0,1,0,1,1,3....]这样子的数组
比如这段信息,我们倾向于对每条数据划分,在检测某个位点的时候,需要考虑到前后文关系,比如我们考虑第三个碱基C,我们需要传递近来计算的特征则是[ACT].
好吧我得承认这个说法仍然足够抽象,用图形的方式来理解,就显得比较容易了

1.1.什么卷积层:
卷积层的这个卷积,在计算机图形学中的应用同样很广泛,而且概念上也是一样的.
其实严格来说,我们这个操作并不能称之为卷积操作,因为数学论文中的卷积操作需要额外的一个步骤就是倒转卷积核,在这里我们仅仅是对固定的层数和区域做运算而已.
在大一的时候,我们接触过滑动窗口算法,用来进行平滑的操作,,或者就像是我们在ps中进行图像处理的时候,所用到的污点修复工具, 也是一种卷积.
这其实就是卷积神经网络中的一部分,只不过严格来说这个操作被称之为pooling(池化)
首先我们要介绍一下卷积核 / 过滤器 / convolution kernel / filtering
就是一个小型矩阵,深度和被卷积对象匹配(为什么这里说被卷积对象而不是输入,这个和我们后面的一个叫做分离卷积的东西有关,当然这个是后话了)
过滤器是怎么样工作的,或者说卷积的数学原理是什么,差不多就这样,那个小的过滤矩阵被称之为核
然后类似滑动窗口的操作,只不过这次窗口被严格限制在了原本张量范围内,窗口的每个计算,对应着目标中一个数字的输出
(图片其实贴在上面了)
例如在这张图中,涉及到了边缘检测的一个简单示例

很好地展现了一个垂直的边缘检测器,这个检测器也是我们常用的类型了
还有一些其他的核
但是迄今为止,我们说到的东西仅仅止步于数学和图形学,神经网络呢???
别急,核心的数目很多,种类很多,能达到的效果都不一样,如果能检测到更适合我们手中样本的数据,就是训练呗.
比如这样一个9*9大小的卷积核心,我们可以设置参数w1--w9, 后面如果有需要还可以使用bias还有激活函数之类的东西进行处理,紧接着根据参数开始训练,这就是我们的一个核心思路.
1.2.卷积层的相关参数
里我们展示一个比较完整的卷积神经网路的图像.
我们可以看到,现在我们的卷积是在三维上进行处理的,每个核的卷积结果都是一个二维矩阵.
如图所示
而具体的计算方法可以是这样子的
在这种比较正常的卷积操作中,我们设置一些相关的参数,并且将他们的名称作为约定俗成
有关参数
n:输入的长宽度
f:卷积核的长宽
s;卷积运算的移动步长
p:填充的长度(注意这个填充长度,不同的材料中表示的含义不太一样)
num:卷积核的数目,卷积核的数目在一般情况下决定了输出的三维张量的频道数量(频道是深度的另一种称呼)
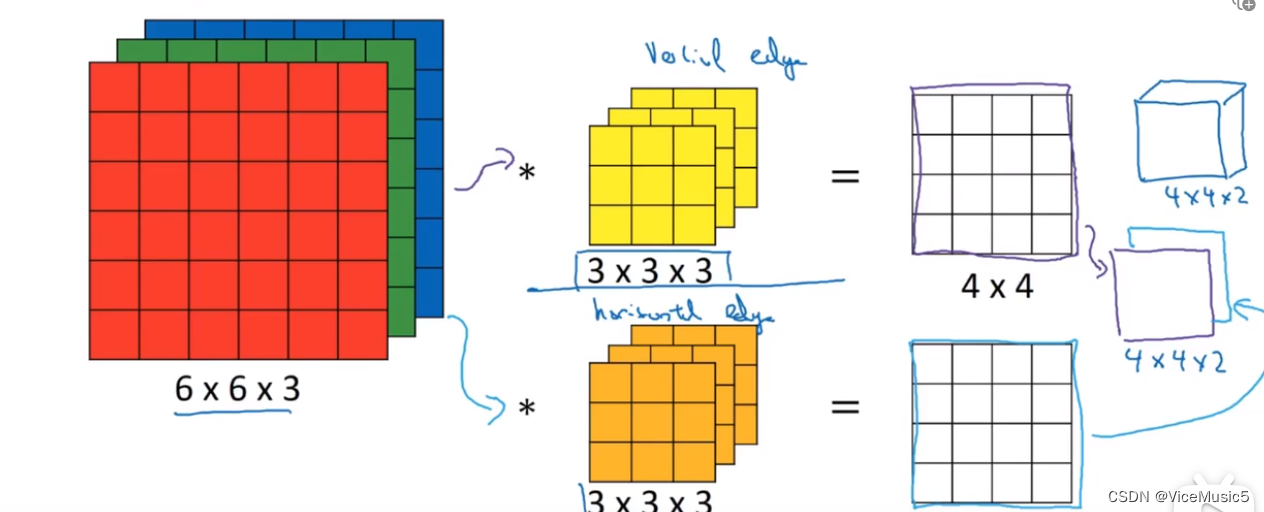
这是一张纯三维的展示图像,途中我们可以看到这里又不止一个卷积核,每个卷积核都能得到一个结果.这里其实存在一个物理意义,每个卷积核都是提取自己需要的特征,比如A获取的是垂直边缘,B获取的是水平边缘.叠加起来就是我们需要的东西(比如轮廓图)
填充和步长
在进行卷积的时候,可以注意到一个问题,随着卷积的增加,虽然特征提取了,但是输出的长宽是肉眼可见的不断变小的.并且步长也会直接影响输出的因素.
而且,卷积也会导致对于边缘部分的采集不充分,所以对于这种情况,我们的处理方法是在原本的输入基础上,在四周填充长度为p的部分,使得卷积出来的结果大小发生一些变化
如图所示

步长

这里还有一个计算公式,通过这个计算公式我们可以得到关于输入和输出的尺寸的区别
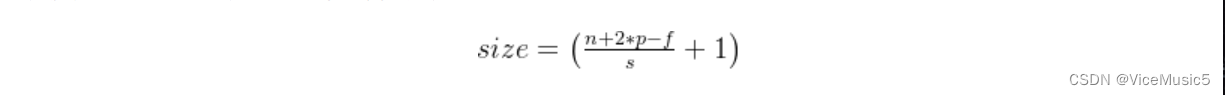
1.3. 什么是池化层
池化层的翻译怎么说呢....汇聚层这个翻译其实更符合语意的
池化层其实个人感觉和卷积没有本质上的区别,都是对局部特征进行提取,然后够获取特征部分,压缩输入,节约计算.或者一些其他的奇奇怪怪的功能.
但是真说计算上的区别,那么就是池化层不需要任何训练参数,比较常用的两个池化核心是最大池化和平均池化. 另外,池化层的特点是,每个池化核心只有一层,这就代表了池化层是不会对输入的通道产生影响,而至少影响尺寸的大小
(另外在这里补充一点通常我们在说有关卷积神经网络的时候,所说的"尺寸"指的是二维尺寸,对于第三维度的高度(我们俗称的Z轴),我们称之为通道数目)
如果说在实际运行代码上的区别,我还记得一个特点就是如果不指定,那么池化层默认自己的步长和核心的尺寸大小一致

如图所示,这个就是池化层中被称之为平均池化层的操作,将自己所在"窗口"内的部分进行加和求平均,剩下最大池化层是干什么应该就不用我多说了.
并且在实际应用中,卷积和池化层中的尺寸计算通常会向下取整,以保持输出结果的整数尺寸
这是因为在卷积和池化操作中,输入特征图的尺寸往往无法被池化窗口或卷积核完全整除。为了保持输出特征图的尺寸与输入特征图的对应关系,并避免信息丢失或产生不连续的特征图,通常会将计算结果向下取整到最接近的整数
1.4,关于CNN的代码简单展示
我们就不使用具体的pytorch的函数和方法来进行过多的展示了,这里直接使用Sequential容器来进行一点简单的展示
# padding如果没有默认为0 ,stride如果不存在默认为1
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), 输出结果为[6,27,27]
nn.Sigmoid(), 进行sigmoid操作,将范围固定在0-1的范围之中
nn.AvgPool2d(kernel_size=2, stride=2), 输出结果为[6,13,13](原本计算结果为13.5,但是向下取整)
nn.Conv2d(6, 16, kernel_size=5), 输出结果为[16,.....]
nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), 输出结果为[16,.....] 嘛.计算结果差不多就这样不算了
nn.Flatten(), #------------------自此开始重新将数据进行展平(如果是大批量数据会保留第一个维度的存在)
nn.Linear(16 * 5 * 5, 120),
nn.Sigmoid(),
nn.Linear(120, 84),
nn.Sigmoid(),
nn.Linear(84, 10))2.关于pytorch中的一些实现代码,参数,以及注意问题
2.1关于具体的神经网络层的api
首先说明一下构建各种类型的卷积层的方法
# 2d的卷积层
nn.Conv2d(in_channels, out_channels, kernel_size=?,padding=?,stride=?)
# 2d的最大池化层
nn.MaxPool2d( kernel_size=?,padding=?,stride=?)
# 2d的平均池化层
nn.AvgPool2d( kernel_size=?,padding=?,stride=?)上面所展示的内容全部都是单一维度的2d,其实还有其他的维度卷积,这里就不加一解释了
里面的参数就不用我多说了
另外这里要单独说明另一个api:ModuleList
2.2关于神经网络层的初始化
神经网络的初始化这里其实要说明一点,就算我们不进行初始化操作,pytorch也会自动进行一些小范围的初始化操作.不过为减少迭代和训练次数,还是有必要的.
因为上面我们引入了有关于ModuleList的东西,所以对于这个使用方法更新的方式,我们需要一点更新,这个是一个具体案例,负责初始化一个携带有ModuleList的块.
def init_weight(m):
if type(m)==nn.Linear or type(m)==nn.Conv2d:
torch.nn.init.constant_(m.bias,0.1)
torch.nn.init.normal_(m.weight,std=0.01)
elif type(m)==nn.ModuleList:
for i,subLayer in enumerate(m):
torch.nn.init.constant_(subLayer.bias,0.1)
torch.nn.init.normal_(subLayer.weight,std=0.01)
self.apply(init_weight)如图所示(注意,无论是sequential容器构建的神经网络,还是通过class类进行构建的,只要是成功继承了nn.Module的神经网络结构部分, 都可以使用这种apply内置接口来对模型,都可以用这种方式来初始化函数,并且对每个模型都进行操作)
对于携带ModuleList的内部类中,我们需要enmuerate函数遍历的操作,然后对内部进行重新的修整.
2.3需要注意的问题
需要注意的问题就是:(长期补充)
1.ModuleLis虽然也是一种容器,但是它真的只是一个存储容器,因此我们无法通过ModuleList进行直接的先前传播计算
这些块在计算的时候会被认为是注册了的层,所以反向传播是可以正常训练的
但是正向转播的时候,这个容器本身是不能进行任何前向传播计算的,需要单独拆出来进行遍历
至于为什么pytorch总能找到哪些神经网络层参与了计算
底层来说,是反向传播机制. 代码上说, pytorch中特有的跟踪机制吧.....
3.关于一些现代神经网络还有内部的实现
其实关于卷积层和卷积层构建的神经网络,其实和密集层,激活函数本质上没什么区别.
但是随着现代神经网络和科学的发展,无论是神经网络本身还是更多的一些需求,我们都扩展出了一些现代的概念和函数架构,在这里我们会简单展示"VGG","NiN","GoogleNet"这三个块形式的结构,并且会在后面拓展一些关于残差等等的东西.
(1)VGG,以及块级别操作的接口
VGG这个名字感觉好怪每次都读成VCC了,.......

其实VGG块没什么太多好讲的,其实本质就是一个简单的卷积神经网络块,通过参数调整来保证无论是输入还输出部分,都能保证通道数目一致.
代码实例如图所示
def vgg_block(num_convs, in_channels, out_channels):
layers = []
for _ in range(num_convs):
layers.append(nn.Conv2d(in_channels, out_channels,
kernel_size=3, padding=1))
layers.append(nn.ReLU())
in_channels = out_channels
layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
return nn.Sequential(*layers)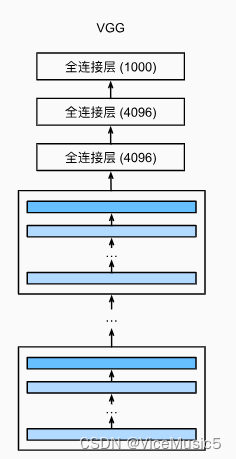
但是这里主要需要解释的就是块级别的网络层,也就是block,这个思想其实就是前向传播实现的,也就是实现了forward接口来实现的结果.至于好处我个人认为有以下两种
-
模块化和可复用性:通过将一组层组织成块的形式,可以将网络的结构划分为更小、更易于管理的模块。这种模块化的设计使得网络的构建更加清晰和可复用。每个块都可以被视为一个独立的单元,可以在不同的网络架构中使用,从而提高代码的可重用性。
-
实现复杂网络架构:块结构可以用于实现一些复杂的网络架构,如残差网络(ResNet)、Inception 网络、U-Net 等。这些网络往往由多个重复的块组成,通过简单的块结构的组合和堆叠,可以构建出具有强大表达能力的网络架构。
(2)NiN
NiN块(network in network)神经网络,其实说真我自己都没有太好的理解

# NiN和其他的网络有一点小小的区别
# 一般的NiN卷积层是一个普通卷积层,一个池化层,两个1*1但是不改变最终尺寸的卷积层
# 前两个就是正常的卷积操作,最后两个池化层的作用就是增加更多的非线性变换
# 提升特征的可提取度
# 卷积层举例:
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
return nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())(3)GoogleNet,以及并行处理,还有inception函数
在进行最后的神经网络计算的时候,我们首先要介绍一个概念,并行操作
其实对于这个操作,其实源自于某一个科研项目(这里指的是我自己),需要处理一个很有特点的数据
一个批次(张量的数据)一共有四个特征,差不多是这个格式
[
[1,2,3,4,5,6,7,8,9,1,2,3,4],[1,2,3,4,5,6,7,8,9,1,2,3,4],
[1,2,3,4,5,6,7,8,9,1,2,3,4],[1,2,3,4,5,6,7,8,9,1,2,3,4]
]每个特征都有自己的特征,而且科研内容的背景环境是完全不同的,所以我们不能使用2d来进行操作
我们需要实现的核心思路就是
首先 , 遍历得到里面的每一个子模块
然后每个子模块计算输入的一部分(张量高级语法),得到一个单独的输出结果
再把这些单独的输出结果重新拼合到张量,作为下一个输入
首先我有一个自己的处理函数写的比较蠢
for i in range(4):
output.append(self.Convs1[i](X[:,i:i+1,:].float()))
X=torch.cat(output,dim=1) #这个dim等于1的压缩机制是啥来着???通过这种方式,我们尝试实现了最简单的Inception模块
(不过在这里,我们的实现方式是ModuleList模块)
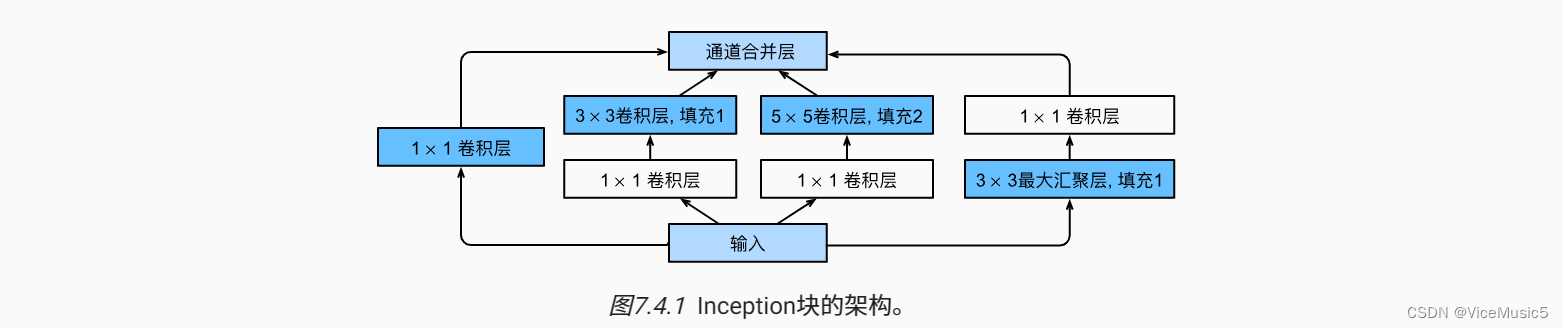
class MyNet(nn.Module):
def __init__(self):
super().__init__()
#创建一个多输入的卷积层
self.Convs1=nn.ModuleList()
#内部传入四个卷积层,卷积以后对每一个层的结果是一个[4,9]
self.Convs1.append(nn.Conv1d(1,1,padding=0,kernel_size=5,stride=1))
self.Convs1.append(nn.Conv1d(1,1,padding=0,kernel_size=5,stride=1))
self.Convs1.append(nn.Conv1d(1,1,padding=0,kernel_size=5,stride=1))
self.Convs1.append(nn.Conv1d(1,1,padding=0,kernel_size=5,stride=1))
# 13 - x +1=9
#创建一个多输入的密集层
self.Convs2=nn.ModuleList()
#内部传入四个密集层 密集计算以后每一个层的结果都是[4,3]
self.Convs2.append(nn.Linear(9,3))
self.Convs2.append(nn.Linear(9,3))
self.Convs2.append(nn.Linear(9,3))
self.Convs2.append(nn.Linear(9,3))
#展平层 [4,3]---->[12]
self.Flatten=nn.Flatten()
#最后一个密集层做处理
self.Linear1=nn.Linear(12,1)
self.init()
#13 - 5 +c1 = 9
#向前传播计算逻辑
def forward(self,X):
output=[]
for i in range(4):
output.append(self.Convs1[i](X[:,i:i+1,:].float()))
X=torch.cat(output,dim=1) #这个dim等于1的压缩机制是啥来着???
output=[]
for i in range(4):
output.append(self.Convs2[i](X[:,i:i+1,:].float()))
X=torch.cat(output,dim=1) #这个dim等于1的压缩机制是啥来着???
X=self.Flatten(X)
X=self.Linear1(X)
return (X)
# 权重初始化函数
def init(self):
def init_weight(m):
if type(m)==nn.Linear or type(m)==nn.Conv2d:
torch.nn.init.constant_(m.bias,0.1)
torch.nn.init.normal_(m.weight,std=0.01)
elif type(m)==nn.ModuleList:
for i,subLayer in enumerate(m):
torch.nn.init.constant_(subLayer.bias,0.1)
torch.nn.init.normal_(subLayer.weight,std=0.01)
self.apply(init_weight)
net=MyNet()(电脑没电了,未完,有空补充)
