【我和Python算法的初相遇】——体验递归的可视化篇

🌈个人主页: Aileen_0v0
🔥系列专栏:PYTHON数据结构与算法学习系列专栏
💫"没有罗马,那就自己创造罗马~" 

目录

递归的起源

什么是递归?

 利用递归解决列表求和问题

递归三定律

递归应用-整数转换为任意进制数

递归可视化 

画一个正方形 

画一个五角星 

画一个九边形 

画圆形

画一个等腰三角形 

利用递归画一个螺旋 

利用递归画一颗分形树 

利用递归画一个谢尔平斯基三角形

递归的起源

递归是一种算法，它利用函数的自身调用来解决问题。递归的历史可以追溯到古代的数学家和逻辑学家，如希腊哲学家亚里士多德和印度数学家阿耶尔巴塔。然而，递归算法的实际应用可以追溯到早期的计算机科学，尤其是在20世纪40年代和50年代的计算机发展初期。

在20世纪初，数学家David Hilbert提出了“希尔伯特问题”，其中包括一个著名的问题——哥德尔不完备定理。这个定理表明，任何一个形式化的系统都无法证明自身完备。这导致了一些数学家开始研究递归函数，因为递归函数是一种强大的工具，可以用来刻画数学中的可计算性概念。在20世纪40年代，递归理论被广泛研究，它为计算机科学的发展奠定了基础。

早期计算机（如ENIAC）是通过执行单个指令来执行操作的，因此递归算法在这些机器上的执行效率较低。然而，随着计算机硬件和编程语言的发展，递归算法变得更加普遍和有效。今天，递归算法被广泛用于计算机科学中的许多应用领域，如数据结构设计、图像处理、机器学习和自然语言处理。

什么是递归?

递归是一种解决问题的方法，其精髓在于将问题分解为规模更小的相同问题持续分解，直到问题规模小到可以用非常简单直接的方式来解决。
递归的问题分解方式非常独特，其算法方面的明显特征就是:在算法流程中调用自身。
递归为我们提供了一种对复杂问题的优雅解决方案，精妙的递归算法常会出奇简单令人赞叹。

问题:

给定一个列表，返回所有数的和列表中数的个数不定，需要一个循环和一个累加变量来迭代求和

def Listsum(nl):
    sum = 0
    for i in nl:
        sum += i
    return sum

print(Listsum([1,2,3,4]))

 利用递归解决列表求和问题

程序很简单，但假如没有循环语句 ?既不能用for，也不能用while还能对不确定长度的列表求和么?

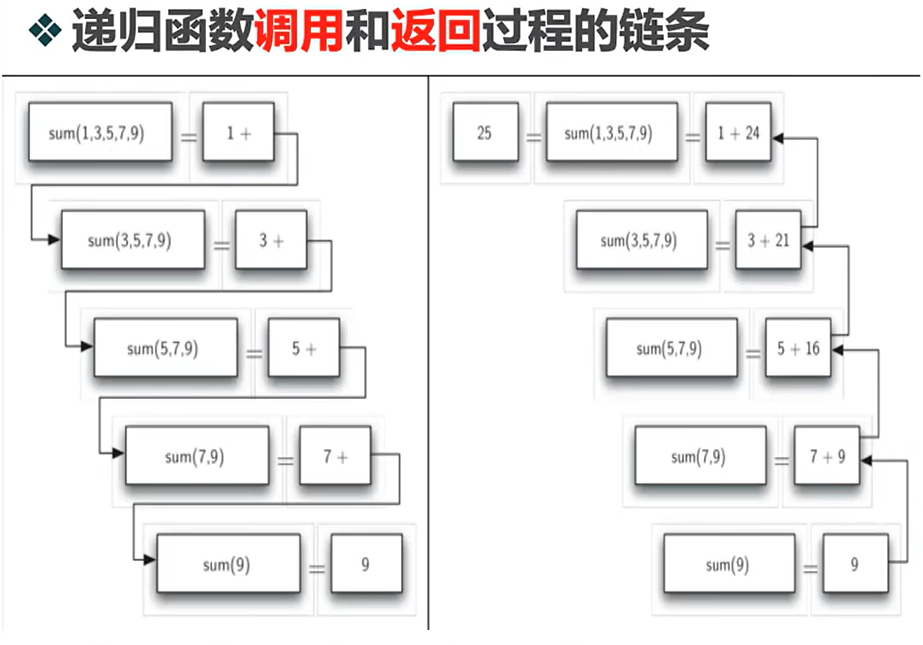
递归三定律

1.结束条件

2.向基态前进

3.自己调用自己

递归应用-整数转换为任意进制数

我们用最熟悉的十进制分析下这个问题

十进制有十个不同符号: convString =0123456789"
比十小的整数，转换成十进制，直接查表就可以了: convString[n] 

比十大的整数，想办法把比十大的整数拆成一系列比十小的整数，逐个查表
比如七百六十九，拆成七、六、九，查表得到769就可以了

所以，在递归三定律里，我们找到了“基，就是小于十的整数本结束条件”

拆解整数的过程就是向“基本结束条件”演进的过程
我们用整数除，和求余数两个计算来将整数一步步拆开除以“进制基base(// base)对“进制基”求余数 (% base)

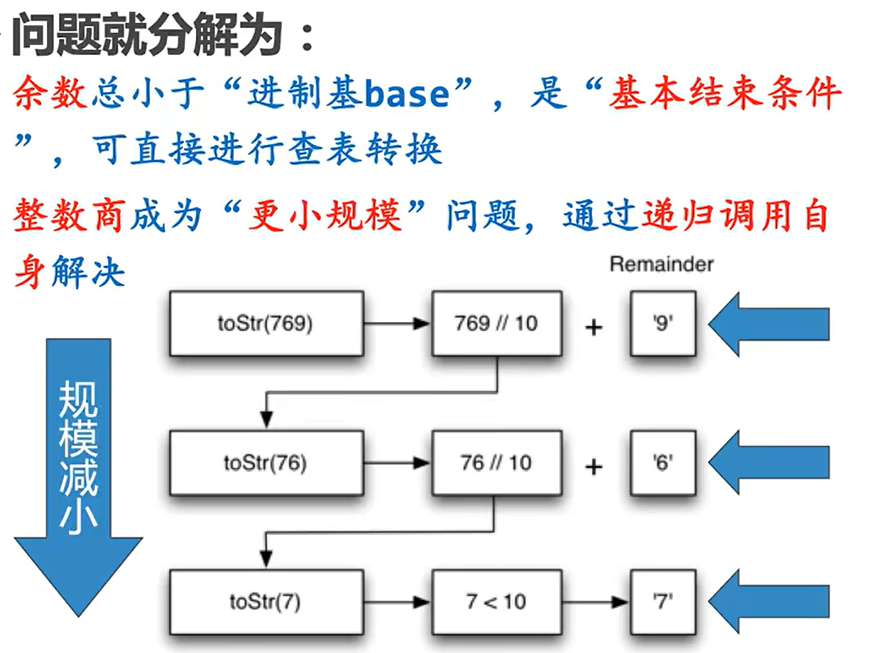
#n为转换的数字   base为进制数
def tostring(n,base):
    coverstring = "0123456789"
    if n < base :
        return coverstring[n]
    else:
        return tostring(n // base , base) + coverstring[n % base]
print(tostring(1999,10))

递归可视化 

画一个正方形 

import turtle
t = turtle.Turtle()
#通过四次向右转90度画一个边长为100的正方形
for i in range(4):
    t.forward(100)
    t.right(90)
turtle.done()

画一个五角星 

#画五角星
import turtle
t = turtle.Turtle()
t.pencolor("red")
t.pensize(3)
for i in range(5):
    t.forward(100)
    t.right(144)
t.hideturtle()

turtle.done()

画一个九边形 

#画九边形
import turtle
t = turtle.Turtle()
t.pencolor("blue")
t.pensize(10)
for i in range(9):
    t.forward(100)
    t.left(320)
t.hideturtle()
turtle.done()

画圆形

#画圆形
import turtle
t = turtle.Turtle()
t.pencolor("blue")
t.pensize(10)
for i in range(1):
    t.circle(180)
t.hideturtle()
turtle.done()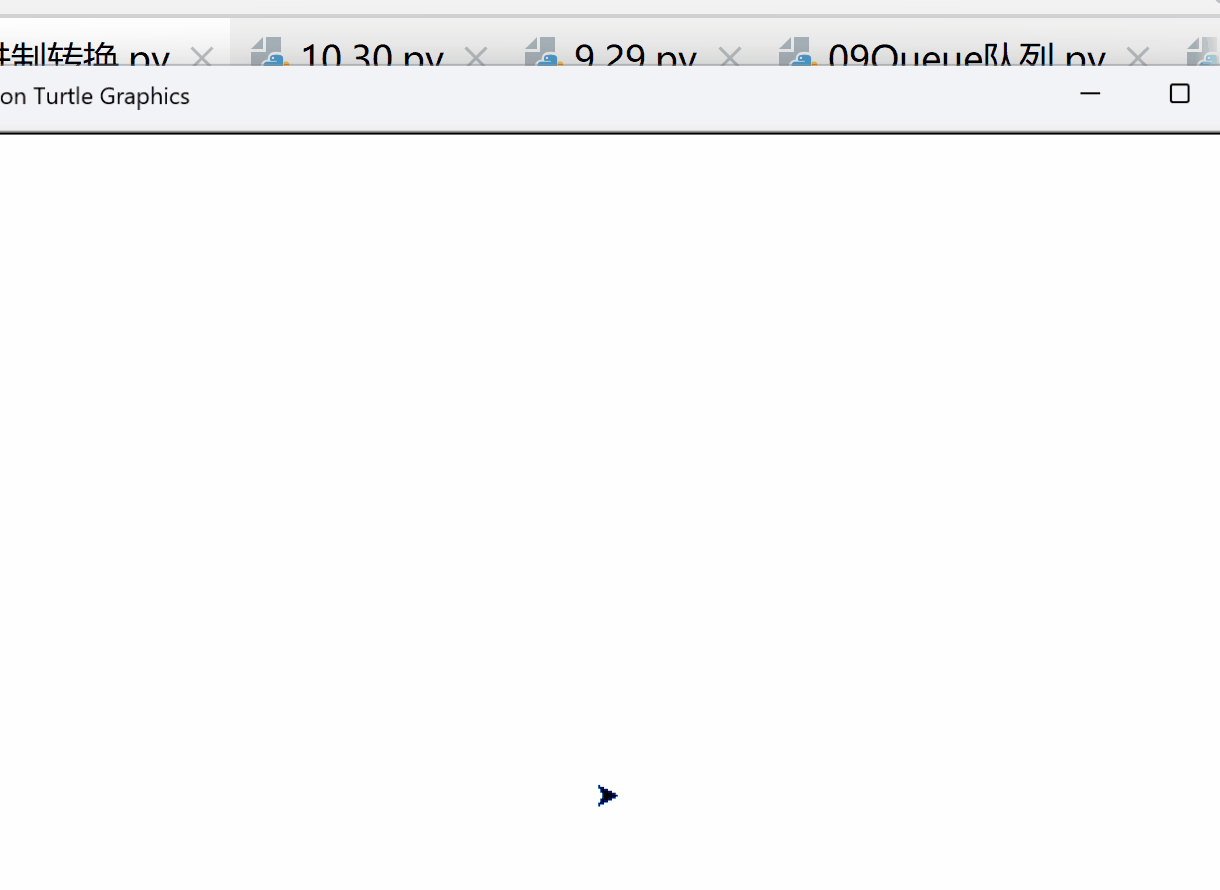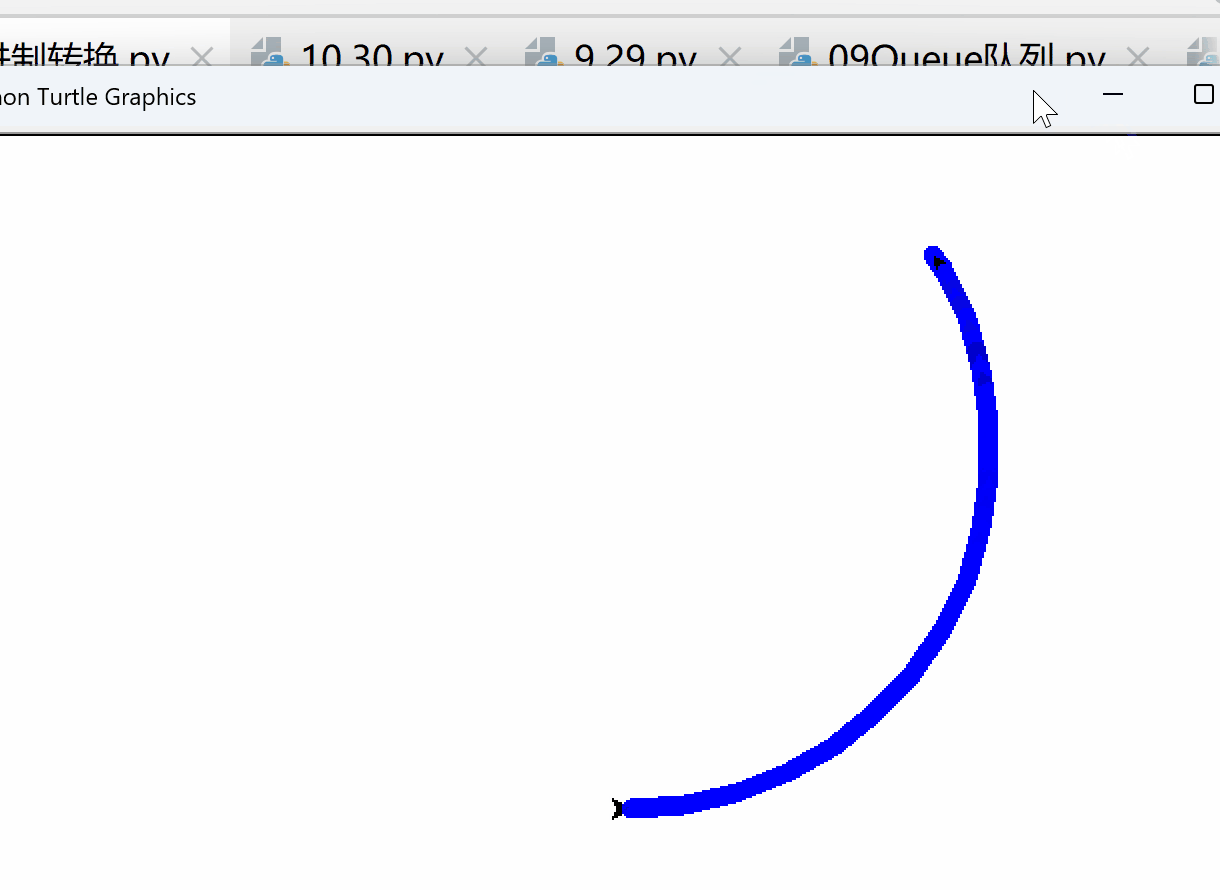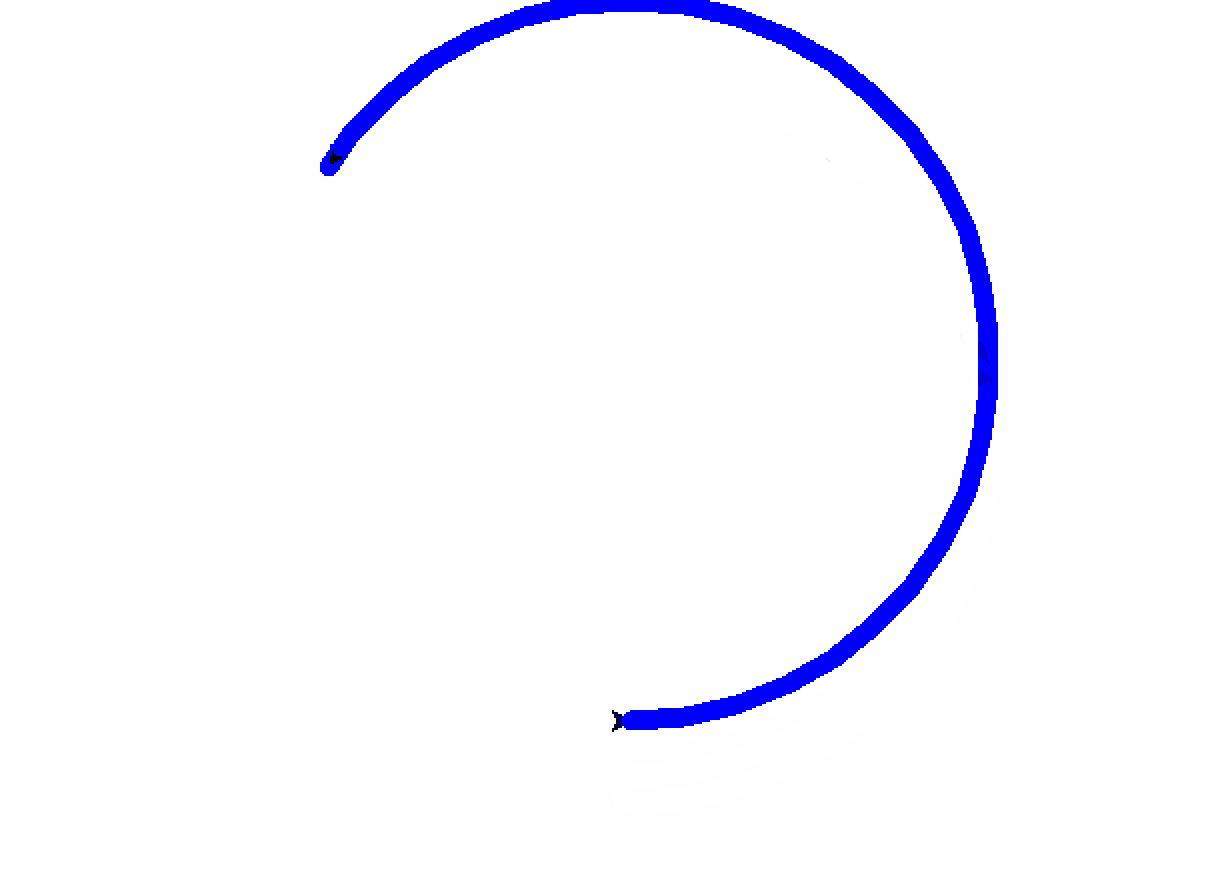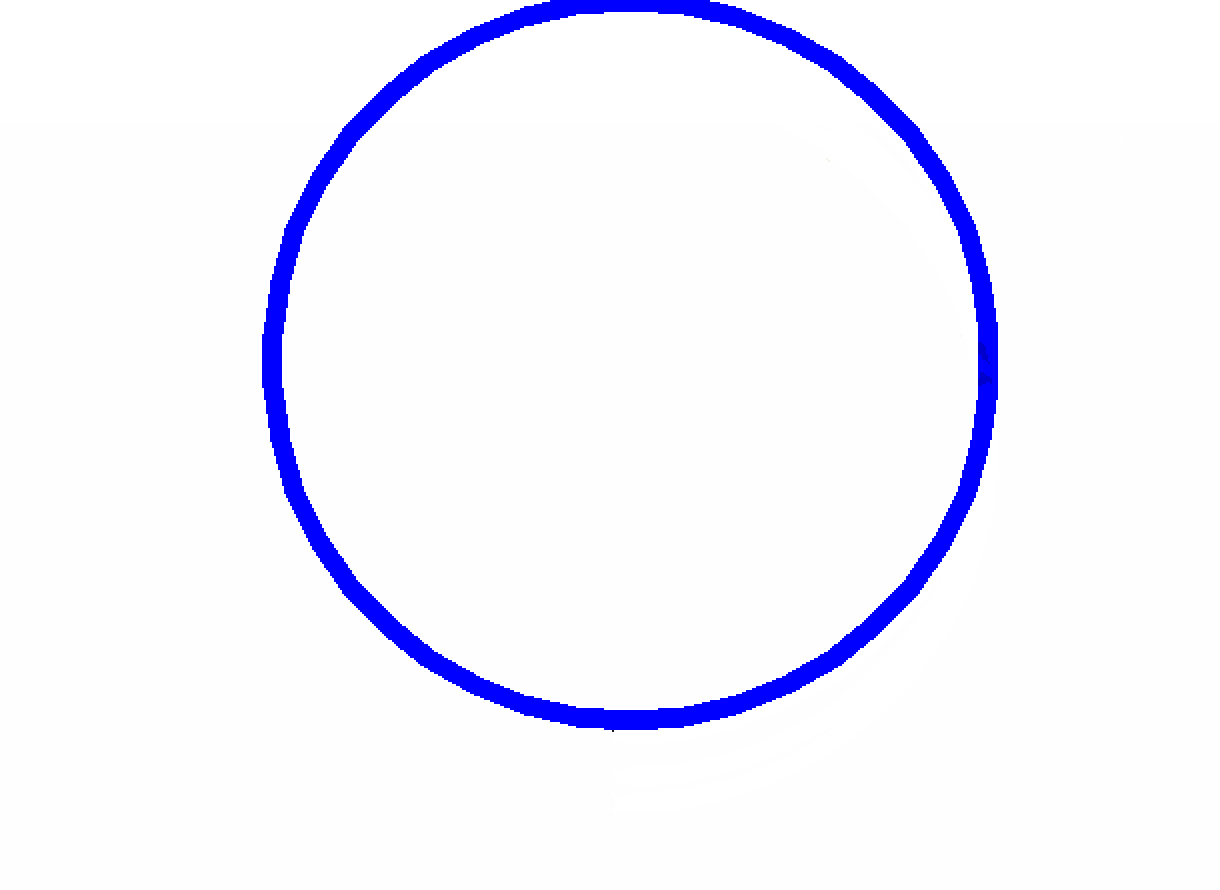

画一个等腰三角形 

#画等腰三角形
import turtle
t = turtle.Turtle()
t.pencolor("blue")
t.pensize(10)
for i in range(4):
    t.forward(100)
    t.left(120)
t.hideturtle()
turtle.done()

利用递归画一个螺旋 

#内置库,用于画图的模块
import turtle
#实例化turtle对象
my_turtle = turtle.Turtle()
#调用窗口
my_win = turtle.Screen()

def draw_spiral(my_turtle,line_len):
    if line_len > 0:
        # 向当前方向走line_len 个像素
        my_turtle.forward(line_len)
        #箭头向右转90度
        my_turtle.left(90)
        #调用自己
        draw_spiral(my_turtle,line_len - 5)
        #♥这个图告诉我们递归不一定要有返回值
draw_spiral(my_turtle,300)
my_win.exitonclick()

利用递归画一颗分形树 

def tree(branch_len, t):
    if branch_len > 5:
        t.forward(branch_len)
        t.right(20)
        tree(branch_len-15, t)
        t.left(40)
        tree(branch_len-15, t)
        t.right(20)
        t.backward(branch_len)

import turtle
t = turtle.Turtle()
my_win = turtle.Screen()
t.left(90)
t.up()
t.backward(200)
t.down()
t.color("black")
tree(110,t)
my_win.exitonclick()

利用递归画一个谢尔平斯基三角形

#绘制谢尔平斯基三角形的辅助函数
import turtle
def draw_triangle(points , color, my_turtle ):
    my_turtle.fillcolor ( color )
    my_turtle.up()
    my_turtle.goto(points[0][0],points[0][1])
    my_turtle.down()
    my_turtle.begin_fill()
    my_turtle.goto(points[1][0],points [1][1])
    my_turtle.goto(points[2][0],points [2][1])
    my_turtle.goto(points[0][0],points [0][1])
    my_turtle.end_fill()

def get_mid(p1,p2 ):
    return ((p1[0] + p2[0]) / 2 , (p1[1] + p2[1]) / 2)

# 绘制谢尔平斯基三角形
def sierpinski(points, degree, my_turtle):
    colormap = [
        "blue",
        "red",
        "green",
        "white",
        "yellow",
        "violet",
        "orange",
    ]
    draw_triangle(points, colormap[degree], my_turtle)
    if degree > 0:
        sierpinski(
            [
                points[0],
                get_mid(points[0], points[1]),
                get_mid(points[0], points[2]),
            ],
            degree - 1,
            my_turtle,
        )
        sierpinski(
            [
                points[1],
                get_mid(points[0],points[1]),
                get_mid(points[1],points[2]),
            ],
            degree - 1,
            my_turtle,
        )
        sierpinski(
            [
                points[2],
                get_mid(points[2],points[1]),
                get_mid(points[0],points[2]),
            ],
            degree - 1,
            my_turtle,
        )

def main():
    my_turtle = turtle.Turtle()
    my_win = turtle.Screen()
    my_points =  [[-100,-50],[0,100],[100,-50]]
    sierpinski(my_points, 5, my_turtle)
    my_win.exitonclick()

print(main())

📝全文总结

本文主要讲解：
    本文主要讲解了递归的历史起源以及使用规则 —— 我们通过递归可以将复杂问题简单化,并且我们还学习了如何通过递归进行进制转换,以及如何通过递归去画出我们想要的图形---螺旋图,分形树,谢尔基三角形。

     今天的干货分享到这里就结束啦！如果觉得文章还可以的话，希望能给个三连支持一下，Aileen的主页还有很多有趣的文章，欢迎小伙伴们前去点评，您的支持就我前进的最大动力！